Medidas de dispersión: rango, varianza y desviación estándar

Recolectar los datos y representarlos en forma de tablas, gráficos y otras distribuciones es esencial para nosotros. Pero también es esencial que tengamos una idea clara de cómo se distribuyen los datos, qué tan dispersos están y cuál es el promedio de los datos. Las medidas de la media no son suficientes para describir los datos y su naturaleza. También necesitamos medir la dispersión en los datos con respecto a diferentes estadísticas de los datos. Por ejemplo, debemos ser capaces de responder a preguntas como, ¿cuánto es la dispersión de la media de los datos circundantes o su mediana? Estos valores nos permiten describir los datos de una mejor manera. Veamos algunos de ellos,

Estas medidas nos dicen

El rango de los datos se da como la diferencia entre los valores máximo y mínimo de las observaciones en los datos. Por ejemplo, digamos que tenemos datos sobre la cantidad de clientes que caminan en la tienda en una semana.

10, 14, 8, 10, 15, 4, 7

Valor mínimo en datos = 7

Valor máximo en los datos = 15

Rango = Valor máximo en los datos – Valor mínimo en los datos

= 15 – 7

= 8

Ahora podemos decir que el rango de los datos es 8. Esto nos da una idea sobre la dispersión de los datos, pero no nos dice cómo se distribuyen.

Diferencia

La varianza de los datos se obtiene midiendo la distancia de los valores observados a la media de la distribución. Aquí no nos interesa el signo de la distancia del punto, nos interesa más la magnitud. Entonces, tomamos cuadrados de la distancia de la media. Digamos que tenemos x ₁ , x ₂ , x ₃ …. x _n como n observaciones y $\bar{x}$ sea la media.

$(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + (x_3 - \bar{x})^2 .... (x_n - \bar{x})^2 = \sum^{n}_{0}(x_i - \bar{x})^2$

Si esta suma es cero, entonces cada término tiene que ser cero, lo que significa que no hay dispersión en los datos. Si es pequeño, significa que los datos se concentran en la media y viceversa para valores grandes de la varianza.

Pero esta medida aún depende del número de observaciones en los datos. Es decir, si hay muchas observaciones, este valor será grande. Entonces, tomamos la media de los datos,

$\text{Variance} = \frac{\sum^{n}_{0}(x_i - \bar{x})^2}{n}\\ \sigma^2 = \frac{\sum^{n}_{0}(x_i - \bar{x})^2}{n}$

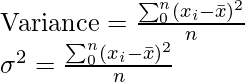
Desviación Estándar

En el cálculo de la varianza, observe que las unidades de la varianza y la unidad de las observaciones no son las mismas. Entonces, para eliminar este problema, definimos la desviación estándar. se denota como $\sigma$

$\sigma = \sqrt{\frac{\sum^{n}_{0}(x_i - \bar{x})^2}{n}}$

Veamos cómo calcular estas medidas en algunos problemas,

Problemas de muestra

Pregunta 1: Averigüe el rango de los siguientes datos:

-4

-10

Solución:

Para calcular el rango de un dato, necesitamos encontrar el máximo y el mínimo de los datos:

Máx = 9

Mínimo = -10

Rango = Máx – Mín

= 9 -(-10)

= 19

Pregunta 2: Encuentra la media y la mediana de los mismos datos:

-4

-10

Solución:

Media de los datos: $\frac{( -4 + 5 -10 + 6 + 9 )}{5}$

= $\frac{6}{5}$

= 1,2

La mediana se llama el elemento medio de los datos.

Mediana = -10.

Pregunta 3: Digamos que tenemos los siguientes datos,

-4

-2

-6

Calcule el rango, la varianza y la desviación estándar de los datos.

Solución:

Rango

Necesitamos encontrar los valores mínimo y máximo de la distribución de datos.

Valor mínimo = -6

Valor máximo = +6

Rango = Valor máximo – Valor mínimo

= 6 – (-6)

= 12

Diferencia

Para encontrar la varianza, primero necesitamos encontrar la media,

Media = $\frac{( -4 + -2 + 0 + -2 + 6 + 4 + 6 + 0 - 6 + 4)}{10}$

= $\frac{6}{10}$

= 0,6

Conocemos la fórmula de la varianza,

Varianza = $\frac{\sum^{n}_{0}(x_i - \bar{x})^2}{n}$

= $\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + (x_3 - \bar{x})^2 .... (x_n - \bar{x})^2}{n}$

= $\frac{(-4 - 0.6)^2 + (-2 - 0.6)^2 + (0 - 0.6)^2 .... }{10}$

= 17,82

Desviación Estándar

$\sigma = \sqrt{\frac{\sum^{n}_{0}(x_i - \bar{x})^2}{n}}$

⇒ $\sigma = \sqrt{17.82}$

⇒ $\sigma = 4.22$

Pregunta 4: Digamos que tenemos los siguientes datos,

-3

Calcule el rango, la varianza y la desviación estándar de los datos.

Solución:

Rango

Necesitamos encontrar los valores mínimo y máximo de la distribución de datos.

Valor mínimo = -3

Valor máximo = +3

Rango = Valor máximo – Valor mínimo

= 3 – (-3)

= 6

Diferencia

Para encontrar la varianza, primero necesitamos encontrar la media,

Media = $\frac{( -3 -3 -3 -3 + 0 + 3 + 3 + 3 +3 )}{10}$

= 0

Conocemos la fórmula de la varianza,

Varianza = $\frac{\sum^{n}_{0}(x_i - \bar{x})^2}{n}$

= $\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + (x_3 - \bar{x})^2 .... (x_n - \bar{x})^2}{n}$

= $\frac{(-3 - 0)^2 + (-3 - 0)^2 + (-3 - 0)^2 + .... }{9}$

= 9

Desviación Estándar

$\sigma = \sqrt{\frac{\sum^{n}_{0}(x_i - \bar{x})^2}{n}}$

⇒ $\sigma = \sqrt{9}$

⇒ $\sigma = 3$

Pregunta 5: Digamos que tenemos los siguientes datos de la cantidad de televisores vendidos por una tienda de electrónica de consumo durante la semana,

Lunes	4
martes	5
miércoles	3
jueves	4
Viernes	5
sábado	5
Domingo	3

Calcule el rango, la varianza y la desviación estándar de los datos.

Solución:

Rango

Necesitamos encontrar los valores mínimo y máximo de la distribución de datos.

Valor mínimo = 3

Valor máximo = +5

Rango = Valor máximo – Valor mínimo

= 5 – (3)

= 2

Diferencia

Para encontrar la varianza, primero necesitamos encontrar la media,

Media = $\frac{( 4 + 5 + 3 + 4 + 5 + 5 +3 )}{10}$

= $\frac{29}{10}$

= 2,9

Conocemos la fórmula de la varianza,

Varianza = $\frac{\sum^{n}_{0}(x_i - \bar{x})^2}{n}$

= $\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + (x_3 - \bar{x})^2 .... (x_n - \bar{x})^2}{n}$

= 0,809

Desviación Estándar

$\sigma = \sqrt{\frac{\sum^{n}_{0}(x_i - \bar{x})^2}{n}}$

⇒ $\sigma = \sqrt{0.809}$

⇒ $\sigma = 0.899$