Método del codo para el valor óptimo de k en KMeans

Requisitos previos: agrupación en clústeres de K-Means
Un paso fundamental para cualquier algoritmo no supervisado es determinar el número óptimo de clústeres en los que se pueden agrupar los datos. El método del codo es uno de los métodos más populares para determinar este valor óptimo de k.
Ahora demostramos el método dado usando la técnica de agrupamiento de K-Means usando la biblioteca Sklearn de python.

Paso 1: Importación de las bibliotecas requeridas

from sklearn.cluster import KMeans
from sklearn import metrics
from scipy.spatial.distance import cdist
import numpy as np
import matplotlib.pyplot as plt

Paso 2: Crear y visualizar los datos

# Creating the data
x1 = np.array([3, 1, 1, 2, 1, 6, 6, 6, 5, 6, 7, 8, 9, 8, 9, 9, 8])
x2 = np.array([5, 4, 5, 6, 5, 8, 6, 7, 6, 7, 1, 2, 1, 2, 3, 2, 3])
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
  
# Visualizing the data
plt.plot()
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('Dataset')
plt.scatter(x1, x2)
plt.show()

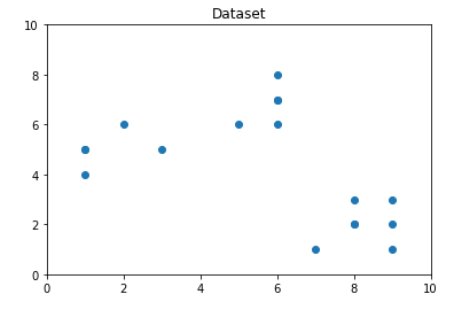
A partir de la visualización anterior, podemos ver que la cantidad óptima de clústeres debe ser alrededor de 3. Pero la visualización de los datos por sí sola no siempre puede dar la respuesta correcta. Por lo tanto, demostramos los siguientes pasos.
Ahora definimos lo siguiente:

1. Distorsión: se calcula como el promedio de las distancias al cuadrado desde los centros de los clústeres respectivos. Por lo general, se utiliza la métrica de distancia euclidiana.
2. Inercia: Es la suma de las distancias al cuadrado de las muestras a su centro de conglomerado más cercano.

Iteramos los valores de k de 1 a 9 y calculamos los valores de distorsiones para cada valor de k y calculamos la distorsión y la inercia para cada valor de k en el rango dado.
Paso 3: Construcción del modelo de agrupamiento y cálculo de los valores de Distorsión e Inercia:

distortions = []
inertias = []
mapping1 = {}
mapping2 = {}
K = range(1, 10)
  
for k in K:
    # Building and fitting the model
    kmeanModel = KMeans(n_clusters=k).fit(X)
    kmeanModel.fit(X)
  
    distortions.append(sum(np.min(cdist(X, kmeanModel.cluster_centers_,
                                        'euclidean'), axis=1)) / X.shape[0])
    inertias.append(kmeanModel.inertia_)
  
    mapping1[k] = sum(np.min(cdist(X, kmeanModel.cluster_centers_,
                                   'euclidean'), axis=1)) / X.shape[0]
    mapping2[k] = kmeanModel.inertia_

Paso 4: Tabulación y Visualización de los resultados
a) Utilizando los diferentes valores de Distorsión:

for key, val in mapping1.items():
    print(f'{key} : {val}')

plt.plot(K, distortions, 'bx-')
plt.xlabel('Values of K')
plt.ylabel('Distortion')
plt.title('The Elbow Method using Distortion')
plt.show()

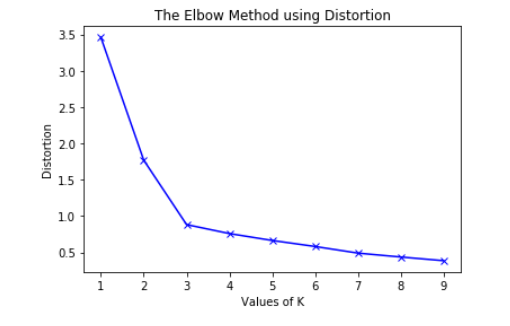
b) Usando los diferentes valores de Inercia:

for key, val in mapping2.items():
    print(f'{key} : {val}')

plt.plot(K, inertias, 'bx-')
plt.xlabel('Values of K')
plt.ylabel('Inertia')
plt.title('The Elbow Method using Inertia')
plt.show()

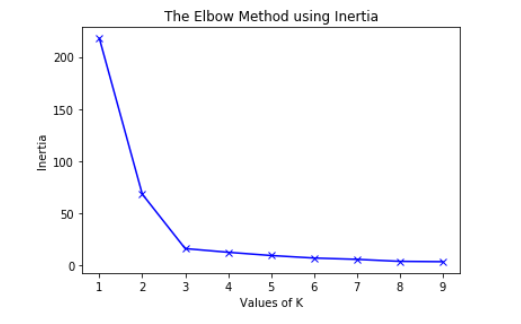
Para determinar el número óptimo de grupos, tenemos que seleccionar el valor de k en el «codo», es decir, el punto después del cual la distorsión/inercia comienza a disminuir de forma lineal. Por lo tanto, para los datos dados, concluimos que el número óptimo de conglomerados para los datos es 3 .
Los puntos de datos agrupados para diferentes valores de k:-
1. k = 1
 

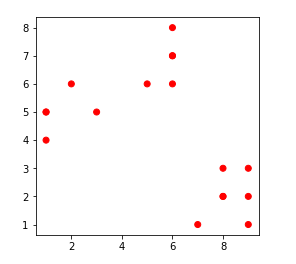
2. k = 2
 

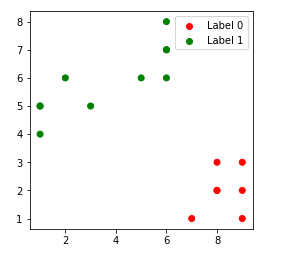
3. k = 3
 

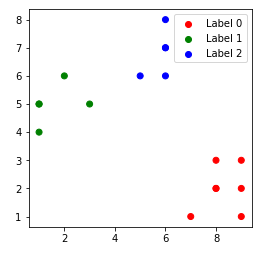
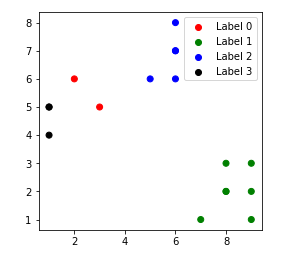
4. k = 4