Mezclar una array dada usando el algoritmo de mezcla de Fisher-Yates

Dada una array, escriba un programa para generar una permutación aleatoria de los elementos de la array. Esta pregunta también se hace como «mezclar una baraja de cartas» o «aleatorizar una array dada». Aquí shuffle significa que cada permutación del elemento de array debería ser igualmente probable. 

Deje que la array dada sea arr[] . Una solución simple es crear una array auxiliar temp[] que inicialmente es una copia de arr[] . Seleccione aleatoriamente un elemento de temp[] , copie el elemento seleccionado aleatoriamente en arr[0] y elimine el elemento seleccionado de temp[] . Repita el mismo proceso n veces y siga copiando elementos a arr[1], arr[2], … . La complejidad temporal de esta solución será O(n^2).

El algoritmo aleatorio de Fisher-Yates funciona en una complejidad de tiempo O(n). La suposición aquí es que se nos da una función rand() que genera un número aleatorio en tiempo O(1). La idea es comenzar desde el último elemento e intercambiarlo con un elemento seleccionado aleatoriamente de toda la array (incluido el último). Ahora considere la array de 0 a n-2 (tamaño reducido en 1) y repita el proceso hasta que lleguemos al primer elemento. 

El siguiente es el algoritmo detallado que es el siguiente:  

To shuffle an array a of n elements (indices 0..n-1):
  for i from n - 1 downto 1 do
       j = random integer with 0 <= j <= i
       exchange a[j] and a[i]

Diagrama de flujo:

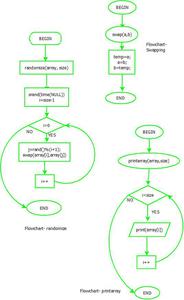
diagrama de flujo

A continuación se muestra una implementación de este algoritmo.

// C++ Program to shuffle a given array
#include<bits/stdc++.h>
#include <stdlib.h>
#include <time.h>
using namespace std;
 
// A utility function to swap to integers
void swap (int *a, int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
 
// A utility function to print an array
void printArray (int arr[], int n)
{
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
    cout << "\n";
}
 
// A function to generate a random
// permutation of arr[]
void randomize (int arr[], int n)
{
    // Use a different seed value so that
    // we don't get same result each time
    // we run this program
    srand (time(NULL));
 
    // Start from the last element and swap
    // one by one. We don't need to run for
    // the first element that's why i > 0
    for (int i = n - 1; i > 0; i--)
    {
        // Pick a random index from 0 to i
        int j = rand() % (i + 1);
 
        // Swap arr[i] with the element
        // at random index
        swap(&arr[i], &arr[j]);
    }
}
 
// Driver Code
int main()
{
    int arr[] = {1, 2, 3, 4, 5, 6, 7, 8};
    int n = sizeof(arr) / sizeof(arr[0]);
    randomize (arr, n);
    printArray(arr, n);
 
    return 0;
}
 
// This code is contributed by
// rathbhupendra

// C Program to shuffle a given array
 
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
 
// A utility function to swap to integers
void swap (int *a, int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
 
// A utility function to print an array
void printArray (int arr[], int n)
{
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("\n");
}
 
// A function to generate a random permutation of arr[]
void randomize ( int arr[], int n )
{
    // Use a different seed value so that we don't get same
    // result each time we run this program
    srand ( time(NULL) );
 
    // Start from the last element and swap one by one. We don't
    // need to run for the first element that's why i > 0
    for (int i = n-1; i > 0; i--)
    {
        // Pick a random index from 0 to i
        int j = rand() % (i+1);
 
        // Swap arr[i] with the element at random index
        swap(&arr[i], &arr[j]);
    }
}
 
// Driver program to test above function.
int main()
{
    int arr[] = {1, 2, 3, 4, 5, 6, 7, 8};
    int n = sizeof(arr)/ sizeof(arr[0]);
    randomize (arr, n);
    printArray(arr, n);
 
    return 0;
}

// Java Program to shuffle a given array
import java.util.Random;
import java.util.Arrays;
public class ShuffleRand
{
    // A Function to generate a random permutation of arr[]
    static void randomize( int arr[], int n)
    {
        // Creating a object for Random class
        Random r = new Random();
         
        // Start from the last element and swap one by one. We don't
        // need to run for the first element that's why i > 0
        for (int i = n-1; i > 0; i--) {
             
            // Pick a random index from 0 to i
            int j = r.nextInt(i+1);
             
            // Swap arr[i] with the element at random index
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
        // Prints the random array
        System.out.println(Arrays.toString(arr));
    }
     
    // Driver Program to test above function
    public static void main(String[] args)
    {
         
         int[] arr = {1, 2, 3, 4, 5, 6, 7, 8};
         int n = arr.length;
         randomize (arr, n);
    }
}
// This code is contributed by Sumit Ghosh

# Python Program to shuffle a given array
from random import randint
 
# A function to generate a random permutation of arr[]
def randomize (arr, n):
    # Start from the last element and swap one by one. We don't
    # need to run for the first element that's why i > 0
    for i in range(n-1,0,-1):
        # Pick a random index from 0 to i
        j = randint(0,i+1)
 
        # Swap arr[i] with the element at random index
        arr[i],arr[j] = arr[j],arr[i]
    return arr
 
# Driver program to test above function.
arr = [1, 2, 3, 4, 5, 6, 7, 8]
n = len(arr)
print(randomize(arr, n))
 
 
# This code is contributed by Pratik Chhajer

// C# Code for Number of digits
// in the product of two numbers
using System;
 
class GFG
{
// A Function to generate a
// random permutation of arr[]
    static void randomize(int []arr, int n)
    {
        // Creating a object
        // for Random class
        Random r = new Random();
         
        // Start from the last element and
        // swap one by one. We don't need to
        // run for the first element
        // that's why i > 0
        for (int i = n - 1; i > 0; i--)
        {
             
            // Pick a random index
            // from 0 to i
            int j = r.Next(0, i+1);
             
            // Swap arr[i] with the
            // element at random index
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
        // Prints the random array
        for (int i = 0; i < n; i++)
        Console.Write(arr[i] + " ");
    }
     
     
// Driver Code
static void Main()
{
    int[] arr = {1, 2, 3, 4,
                 5, 6, 7, 8};
    int n = arr.Length;
    randomize (arr, n);
}
}
 
// This code is contributed by Sam007

<?php
// PHP Program to shuffle
// a given array
 
// A function to generate
// a random permutation of arr[]
function randomize ($arr, $n)
{
    // Start from the last element
    // and swap one by one. We
    // don't need to run for the
    // first element that's why i > 0
    for($i = $n - 1; $i >= 0; $i--)
    {
        // Pick a random index
        // from 0 to i
        $j = rand(0, $i+1);
 
        // Swap arr[i] with the
        // element at random index
        $tmp = $arr[$i];
        $arr[$i] = $arr[$j];
        $arr[$j] = $tmp;
    }
    for($i = 0; $i < $n; $i++)
    echo $arr[$i]." ";
}
 
// Driver Code
$arr = array(1, 2, 3, 4,
             5, 6, 7, 8);
$n = count($arr);
randomize($arr, $n);
 
// This code is contributed by mits
?>

<script>
// JavaScript Program to shuffle a given array
 
// A function to print an array
let printArray = (arr, n)=>
{
    ans = '';
    for (let i = 0; i < n; i++)
    {
        ans += arr[i] + " ";
    }
    console.log(ans);
}
 
// A function to generate a random
// permutation of arr
let randomize = (arr, n) =>
{
 
    // Start from the last element and swap
    // one by one. We don't need to run for
    // the first element that's why i > 0
    for (let i = n - 1; i > 0; i--)
    {
     
        // Pick a random index from 0 to i inclusive
        let j = Math.floor(Math.random() * (i + 1));
 
        // Swap arr[i] with the element
        // at random index
        [arr[i], arr[j]] = [arr[j], arr[i]];
    }
}
 
// Driver Code
let arr = [1, 2, 3, 4, 5, 6, 7, 8];
let n = arr.length;
randomize (arr, n);
printArray(arr, n);
 
// This code is contributed by rohitsingh07052.
</script>

Producción : 
 

7 8 4 6 3 1 2 5

La función anterior asume que rand() genera un número aleatorio. 

Complejidad de Tiempo: O(n), asumiendo que la función rand() toma O(1) tiempo., Espacio Auxiliar: O(1)

¿Como funciona esto? 

La probabilidad de que el i-ésimo elemento (incluido el último) vaya a la última posición es 1/n, porque elegimos un elemento al azar en la primera iteración.
Se puede demostrar que la probabilidad de que el i-ésimo elemento vaya a la penúltima posición es 1/n dividiéndola en dos casos. 
Caso 1: i = n-1 (índice del último elemento) : 
La probabilidad de que el último elemento vaya a la penúltima posición es = (probabilidad de que el último elemento no permanezca en su posición original) x (probabilidad de que el índice seleccionado en la posición anterior el paso se elige de nuevo para que el último elemento se intercambie) 
Así que la probabilidad = ((n-1)/n) x (1/(n-1)) = 1/n 
Caso 2: 0 < i < n-1 ( índice de no último) : 
La probabilidad de que el i-ésimo elemento vaya a la segunda posición = (probabilidad de que el i-ésimo elemento no se elija en la iteración anterior) x (probabilidad de que el i-ésimo elemento se elija en esta iteración) 
Entonces, la probabilidad = ((n-1)/n) x (1 /(n-1)) = 1/n
Podemos generalizar fácilmente la prueba anterior para cualquier otra posición.

https://www.youtube.com/playlist?list=PLqM7alHXFySEQDk2MDfbwEdjd2svVJH9p

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.