Dado un número entero N que denota la longitud de un palo dado, la tarea es minimizar el tiempo requerido para dividir el palo en pedazos de una unidad de longitud, dado que es posible un solo corte para cualquier porción de palo en cualquier instante de tiempo.
Ejemplos:
Entrada: N = 100
Salida: 7
Explicación:
(100 unidades) —> (2 porciones de 50 unidades) —> (4 porciones de 25 unidades) —> (4 porciones de 12 unidades, 4 porciones de 13 unidades) —> ( 12 porciones de 6 unidades, 4 porciones de 7 unidades) —> (28 porciones de 3 unidades, 4 porciones de 4 unidades) —> (28 porciones de 1 unidad, 36 porciones de 2 unidades) —> (100 porciones de 1 unidad) )Entrada: N = 65
Salida: 7
Explicación:
(65 unidades) —> (1 porción de 32 unidades, 1 porción de 33 unidades) —> (3 porciones de 16 unidades, 1 porción de 17 unidades) —> (7 porciones de 8 unidades, 1 raciones de 9 unidades) —> (15 raciones de 4 unidades, 1 ración de 5 unidades) —> (31 raciones de 2 unidades, 1 raciones de 3 unidades) —> (63 raciones de 1 unidad, 1 ración de 2 unidades) —> (65 porciones de 1 unidad)
Enfoque:
dado que podemos cortar cualquier porción del palo una vez en un momento determinado, debemos maximizar las porciones después de cada corte. Así, cortaremos el palo en dos partes de la mayor longitud posible con el primer corte. En el siguiente caso, corte más las dos partes obtenidas en dos partes más largas cada una en el siguiente corte. Repita esto hasta obtener N piezas unitarias.
Ilustración:
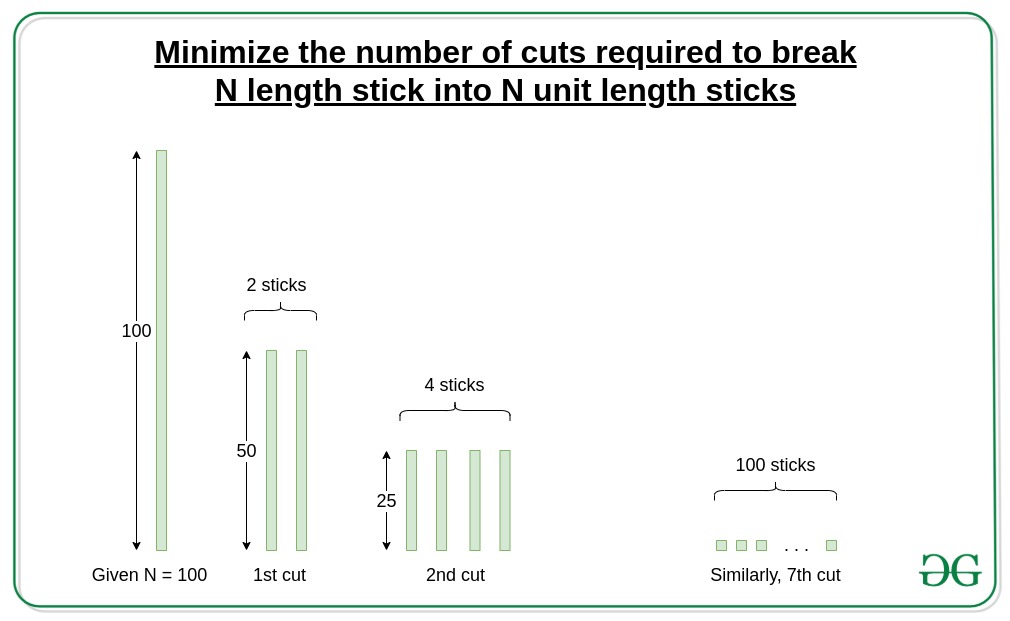
N = 100
1er Corte: (50) + (50)
2do Corte: (25) + (25) + (25) + (25)
3er Corte: (12) + (13) + (12) + (13) ) + (12) + (13) + (12) + (13)
4to Corte: (6) + (6) + (6) + (7) + (6) + (6) + (6) + (7 ) + (6) + (6) + (6) + (7) + (6) + (6) + (6) + (7)
5to Corte: (3) + (3) + (3) + (3 ) + (3) + (3) + (3) + (4) + (3) + (3) + (3) + (3) + (3) + (3) + (3) + (4) + (3) + (3) + (3) + (3) + (3) + (3) + (3) + (4) + (3) + (3) + (3) + (3) + (3) ) + (3) + (3) + (4)
6° Corte: 28 porciones de 1 unidad, 36 porciones de 2 unidades
7° Corte: 100 porciones de 1 unidad
Por lo tanto, el tiempo mínimo requerido para dividir un palo de N longitud en piezas de 1 unidad es ceil(log 2 N) .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find minimum
// time required to split a
// stick of N length into
// unit pieces
#include <bits/stdc++.h>
using namespace std;
// Function to return the
// minimum time required
// to split stick of N into
// length into unit pieces
int min_time_to_cut(int N)
{
if (N == 0)
return 0;
// Return the minimum
// unit of time required
return ceil(log2(N));
}
// Driver Code
int main()
{
int N = 100;
cout << min_time_to_cut(N);
return 0;
}
Java
// Java program to find minimum
// time required to split a
// stick of N length into
// unit pieces
import java.lang.*;
class GFG{
// Function to return the
// minimum time required
// to split stick of N into
// length into unit pieces
static int min_time_to_cut(int N)
{
if (N == 0)
return 0;
// Return the minimum
// unit of time required
return (int)Math.ceil(Math.log(N) /
Math.log(2));
}
// Driver Code
public static void main(String[] args)
{
int N = 100;
System.out.print(min_time_to_cut(N));
}
}
// This code is contributed by rock_cool
Python3
# Python3 program to find minimum # time required to split a stick # of N length into unit pieces import math # Function to return the # minimum time required # to split stick of N into # length into unit pieces def min_time_to_cut(N): if (N == 0): return 0 # Return the minimum # unit of time required return int(math.log2(N)) + 1 # Driver Code N = 100 print(min_time_to_cut(N)) # This code is contributed by Vishal Maurya
C#
// C# program to find minimum
// time required to split a
// stick of N length into
// unit pieces
using System;
class GFG{
// Function to return the
// minimum time required
// to split stick of N into
// length into unit pieces
static int min_time_to_cut(int N)
{
if (N == 0)
return 0;
// Return the minimum
// unit of time required
return (int)Math.Ceiling(Math.Log(N) /
Math.Log(2));
}
// Driver Code
public static void Main()
{
int N = 100;
Console.Write(min_time_to_cut(N));
}
}
// This code is contributed by Code_Mech
Javascript
<script>
// Javascript program to find minimum
// time required to split a stick of
// N length into unit pieces
// Function to return the
// minimum time required
// to split stick of N into
// length into unit pieces
function min_time_to_cut(N)
{
if (N == 0)
return 0;
// Return the minimum
// unit of time required
return Math.ceil(Math.log(N) /
Math.log(2));
}
// Driver code
let N = 100;
document.write(min_time_to_cut(N));
// This code is contributed by divyesh072019
</script>
7
Complejidad Temporal: O (1)
Espacio Auxiliar: O (1)
Publicación traducida automáticamente
Artículo escrito por CharchitKapoor y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA