Minimizar la diferencia entre dos secuencias obtenidas al dividir las primeras N potencias de 2

Dado un número par positivo N , la tarea es dividir las primeras N potencias de 2 en dos secuencias iguales de modo que se minimice la diferencia absoluta entre su suma. Imprime la diferencia mínima obtenida.

Ejemplos: 
 

Entrada: N = 2
Salida: 2
Explicación:
La secuencia es {2, 4}.
La única forma posible de dividir la secuencia es {2}, {4}. Por lo tanto, diferencia = 4 − 2 = 2.

Entrada: N = 4
Salida: 6
Explicación:
La secuencia es {2, 4, 8, 16}.
La forma más óptima es dividir la secuencia como {2, 16}, {4, 8}. La diferencia es (2 + 16) − (4 + 8) = 6.

Enfoque ingenuo: el enfoque más simple para resolver este problema es generar todas las combinaciones posibles de N/2 elementos de la secuencia y almacenar su suma. Luego, encuentra la diferencia mínima entre todas las sumas de los pares. 
Complejidad temporal: O(2 ^N )
Espacio auxiliar: O(N)

Enfoque: El enfoque anterior también se puede optimizar según las siguientes observaciones:

• Como 2 ^N es mayor que la suma de todos los demás elementos combinados:

• El subarreglo que tiene el elemento más grande siempre tendrá una suma mayor. Por lo tanto, para minimizar las diferencias entre su suma, la idea es colocar los (N/2 – 1) elementos más pequeños en el subarreglo con el elemento más grande.

Siga los pasos a continuación para resolver el problema:

• Inicialice dos variables, sum1 = 0 y sum2 = 0 , para almacenar la suma del primer subarreglo y el segundo subarreglo respectivamente.
• Agregue la suma de 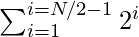 y 2 ^N a la variable sum1 .
• Agregue la suma de 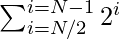 a la variable sum2 .
• Después de completar los pasos anteriores, imprima la diferencia entre sum1 y sum2 .

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to partition first N powers
// of 2 into two subsequences with
// minimum difference between their sum
void minimumDifference(int N)
{
    // Largest element in the first part
    int sum1 = (1 << N), sum2 = 0;
 
    // Place N/2 - 1 smallest
    // elements in the first sequence
    for (int i = 1; i < N / 2; i++)
        sum1 += (1 << i);
 
    // Place remaining N / 2 elements
    // in the second sequence
    for (int i = N / 2; i < N; i++)
        sum2 += (1 << i);
 
    // Print the minimum difference
    cout << sum1 - sum2;
}
 
// Driver Code
int main()
{
    int N = 4;
    minimumDifference(N);
 
    return 0;
}

// Java implementation of
// the above approach
import java.util.*;
class GFG
{
 
 // Function to partition first N powers
  // of 2 into two subsequences with
  // minimum difference between their sum
  static void minimumDifference(int N)
  {
     
    // Largest element in the first part
    int sum1 = (1 << N), sum2 = 0;
  
    // Place N/2 - 1 smallest
    // elements in the first sequence
    for (int i = 1; i < N / 2; i++)
      sum1 += (1 << i);
  
    // Place remaining N / 2 elements
    // in the second sequence
    for (int i = N / 2; i < N; i++)
      sum2 += (1 << i);
  
    // Print the minimum difference
    System.out.println(sum1 - sum2);
  }
 
    // Driver Code
    public static void main(String args[])
    {
        int N = 4;
        minimumDifference(N);
    }
}
 
// This code is contributed by splevel62.

# Python program for the above approach
 
# Function to partition first N powers
# of 2 into two subsequences with
# minimum difference between their sum
def minimumDifference(N):
   
    # Largest element in the first part
    sum1 = (1 << N)
    sum2 = 0
 
    # Place N/2 - 1 smallest
    # elements in the first sequence
    for i in range(1, N // 2):
        sum1 += (1 << i)
 
    # Place remaining N / 2 elements
    # in the second sequence
    for i in range( N // 2, N):
        sum2 += (1 << i)
 
    # Print the minimum difference
    print(sum1 - sum2)
     
# Driver Code
N = 4
minimumDifference(N)
 
# This code is contributed by rohitsingh07052.

// C# program for the above approach
using System;
class GFG
{
 
  // Function to partition first N powers
  // of 2 into two subsequences with
  // minimum difference between their sum
  static void minimumDifference(int N)
  {
    // Largest element in the first part
    int sum1 = (1 << N), sum2 = 0;
 
    // Place N/2 - 1 smallest
    // elements in the first sequence
    for (int i = 1; i < N / 2; i++)
      sum1 += (1 << i);
 
    // Place remaining N / 2 elements
    // in the second sequence
    for (int i = N / 2; i < N; i++)
      sum2 += (1 << i);
 
    // Print the minimum difference
    Console.WriteLine(sum1 - sum2);
  }
 
  // Driver Code
  static public void Main ()
  {
    int N = 4;
    minimumDifference(N);
  }
}
 
// This code is contributed by susmitakundugoaldanga.

<script>
 
// JavaScript implementation of
// the above approach
 
    // Function to partition first N powers
    // of 2 into two subsequences with
    // minimum difference between their sum
    function minimumDifference(N) {
 
        // Largest element in the first part
        var sum1 = (1 << N), sum2 = 0;
 
        // Place N/2 - 1 smallest
        // elements in the first sequence
        for (i = 1; i < N / 2; i++)
            sum1 += (1 << i);
 
        // Place remaining N / 2 elements
        // in the second sequence
        for (i = N / 2; i < N; i++)
            sum2 += (1 << i);
 
        // Print the minimum difference
        document.write(sum1 - sum2);
    }
 
    // Driver Code
     
        var N = 4;
        minimumDifference(N);
 
// This code contributed by aashish1995
 
</script>

6

Complejidad temporal: O(N)
Espacio auxiliar: O(1)