Dada una string binaria S de longitud N que consta de 0s , 1s y “?” , donde «?» puede ser reemplazado por 0 o 1 , la tarea es contar la suma de los intercambios mínimos de caracteres adyacentes requeridos para ordenar todos los arreglos posibles de la string en orden no decreciente Dado que la respuesta puede ser muy grande, imprímala módulo 10 9 + 7 .
Ejemplos:
Entrada: S = “?0?”
Salida: 3
Explicación:
Los posibles reordenamientos de las strings dadas son {“101”, “100”, “000”, “001”}.
Swaps mínimos para hacer “101” no decreciente, es decir “011” = 1.
Swaps mínimos para hacer “100” no decreciente, es decir “001” = 2.
Swaps mínimos para hacer “000” no decreciente, es decir “000 ” = 0.
Los swaps mínimos para hacer que “001” no disminuya, es decir, “001” = 0.
Por lo tanto, el total de swaps necesarios es 3.Entrada: S = “1?00?”
Salida: 17
Enfoque: Considere la siguiente representación de string: <Alguna string binaria> 1 <Alguna string que tenga un número de 0 y un número b de?>
- Para cada ‘0’ a su derecha, hay una inversión para cada string binaria generada para cada signo de interrogación. Entonces, las inversiones aquí son a*2 b .
- Para el signo de interrogación, hay
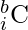formas de elegir, de modo que hay i número de 0 y para cada uno de ellos hay i inversiones. - Hay un total de
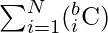
- La expresión anterior se puede transformar en b*2 (b – 1) . Si no hay “?” en la string, el valor es 0 .
- Allí se ha contado el “1” para un total de una inversión * 2 b + b*2 (b – 1) .
- Para todos «?» a la izquierda de “1”, multiplique el valor anterior por 2, ya que un “?” generaría dos strings nuevas por cada string existente contada.
- Después de atravesar toda la string, devuelva el conteo.
Siga los pasos a continuación para resolver el problema:
- Inicialice una cuenta variable como 0 para almacenar la suma de los intercambios mínimos totales requeridos para todas las strings posibles.
- Atraviese la string binaria de manera inversa .
- Para cada “1” en la string, calcule el producto de la cuenta de 0 y 2 (cuenta de ?) , es decir, calcule el valor de la cuenta como a * 2 b + b * 2 (b – 1) .
- Si el carácter actual es «0» , entonces aumente la cuenta de 0 s.
- De lo contrario, multiplique el valor de la cuenta por 2 y repita el proceso anterior.
- Después de completar los pasos anteriores, imprima el valor de conteo como resultado.
A continuación se muestra la implementación del enfoque anterior:
C++14
// C++ program for the above approach
#include<bits/stdc++.h>
#define MOD 1000000007
using namespace std;
// Precalculate the values of power of 2
vector<int> MEM = { 1, 2, 4, 8, 16, 32, 64,
128, 256, 512, 1024,
2048, 4096 };
// Function to calculate 2 ^ N % mod
int mod_pow2(int n)
{
while (n >= MEM.size())
MEM.push_back((MEM[-1] * 2) % MOD);
return MEM[n];
}
// Function to find sum of inversions
int inversions(string bstr)
{
// Initialise a list of 0s and ?s
int total = 0, zeros = 0, questions = 0;
// Traverse the string in the
// reversed manner
reverse(bstr.begin(),bstr.end());
for(char x: bstr)
{
int q;
// If the current character is 1
if (x == '1')
{
// Effectively calculate a * b^(b-1)
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
}
// If the current character is 0
else if (x == '0')
{
//Increment count of zeroes
zeros += 1;
}
else
{
// Double count the zeroes
total *= 2;
// Find b * 2^(b-1)
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
// Increment count of questions
questions += 1;
}
}
// Return the final count
return total;
}
// Driver Code
int main()
{
// Given string S
string S = "?0?";
// Function Call
cout << inversions(S);
}
// This code is contributed by mohit kumar 29
Java
// Java program for the above approach
import java.io.*;
import java.util.*;
class GFG{
static int MOD = 1000000007;
static Integer array[] = { 1, 2, 4, 8, 16, 32, 64,
128, 256, 512, 1024,
2048, 4096 };
// Precalculate the values of power of 2
static Vector<Integer> MEM = new Vector<Integer>(
Arrays.asList(array));
// Function to calculate 2 ^ N % mod
static int mod_pow2(int n)
{
while (n >= MEM.size())
MEM.add((MEM.get(
MEM.size() - 1) * 2) % MOD);
return MEM.get(n);
}
// Function to find sum of inversions
static int inversions(char[] bstr)
{
// Initialise a list of 0s and ?s
int total = 0, zeros = 0, questions = 0;
// Traverse the string in the
// reversed manner
int j = bstr.length - 1;
for(int i = 0; i < bstr.length / 2; i++)
{
char temp = bstr[i];
bstr[i] = bstr[j];
bstr[j] = temp;
j--;
}
for(char x : bstr)
{
int q;
// If the current character is 1
if (x == '1')
{
// Effectively calculate a * b^(b-1)
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
}
// If the current character is 0
else if (x == '0')
{
// Increment count of zeroes
zeros += 1;
}
else
{
// Double count the zeroes
total *= 2;
// Find b * 2^(b-1)
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
// Increment count of questions
questions += 1;
}
}
// Return the final count
return total;
}
// Driver Code
public static void main(String[] args)
{
// Given string S
char S[] = "?0?".toCharArray();
// Function Call
System.out.println(inversions(S));
}
}
// This code is contributed by divyeshrabadiya07
Python3
# Python3 program for the above approach MOD = 10**9 + 7 # Precalculate the values of power of 2 MEM = [1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096] # Function to calculate 2 ^ N % mod def mod_pow2(n): while n >= len(MEM): MEM.append((MEM[-1] * 2) % MOD) return MEM[n] # Function to find sum of inversions def inversions(bstr): # Initialise a list of 0s and ?s total, zeros, questions = (0, )*3 # Traverse the string in the # reversed manner for x in reversed(bstr): # If the current character is 1 if x == '1': # Effectively calculate a * b^(b-1) z = zeros * mod_pow2(questions) if questions == 0: q = 0 else: q = questions * mod_pow2(questions - 1) total = (total + z + q) % MOD # If the current character is 0 elif x == '0': # Increment count of zeroes zeros += 1 else: # Double count the zeroes total *= 2 # Find b * 2^(b-1) z = zeros * mod_pow2(questions) if questions == 0: q = 0 else: q = questions * mod_pow2(questions - 1) total = (total + z + q) % MOD # Increment count of questions questions += 1 # Return the final count return total # Driver Code def main(): # Given string S S = "?0?" # Function Call print(inversions(S)) if __name__ == "__main__": main()
C#
// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG {
static int MOD = 1000000007;
// Precalculate the values of power of 2
static List<int> MEM = new List<int>(new int[] { 1, 2, 4, 8, 16, 32, 64,
128, 256, 512, 1024,
2048, 4096 });
// Function to calculate 2 ^ N % mod
static int mod_pow2(int n)
{
while (n >= MEM.Count)
MEM.Add((MEM[MEM.Count - 1] * 2) % MOD);
return MEM[n];
}
// Function to find sum of inversions
static int inversions(char[] bstr)
{
// Initialise a list of 0s and ?s
int total = 0, zeros = 0, questions = 0;
// Traverse the string in the
// reversed manner
Array.Reverse(bstr);
foreach(char x in bstr)
{
int q;
// If the current character is 1
if (x == '1')
{
// Effectively calculate a * b^(b-1)
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
}
// If the current character is 0
else if (x == '0')
{
// Increment count of zeroes
zeros += 1;
}
else
{
// Double count the zeroes
total *= 2;
// Find b * 2^(b-1)
int z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(
questions - 1);
total = (total + z + q) % MOD;
// Increment count of questions
questions += 1;
}
}
// Return the final count
return total;
}
// Driver code
static void Main()
{
// Given string S
char[] S = "?0?".ToCharArray();
// Function Call
Console.WriteLine(inversions(S));
}
}
// This code is contributed by divyesh072019
Javascript
<script>
// Javascript program for the above approach
let MOD = 1000000007;
// Precalculate the values of power of 2
let MEM = [ 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096 ];
// Function to calculate 2 ^ N % mod
function mod_pow2(n)
{
while (n >= MEM.length)
MEM.push((MEM[MEM.length - 1] * 2) % MOD);
return MEM[n];
}
// Function to find sum of inversions
function inversions(bstr)
{
// Initialise a list of 0s and ?s
let total = 0, zeros = 0, questions = 0;
// Traverse the string in the
// reversed manner
bstr.reverse();
for(let i = 0; i < bstr.length; i++)
{
let q;
// If the current character is 1
if (bstr[i] == '1')
{
// Effectively calculate a * b^(b-1)
let z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(questions - 1);
total = (total + z + q) % MOD;
}
// If the current character is 0
else if (bstr[i] == '0')
{
// Increment count of zeroes
zeros += 1;
}
else
{
// Double count the zeroes
total *= 2;
// Find b * 2^(b-1)
let z = zeros * mod_pow2(questions);
if (questions == 0)
q = 0;
else
q = questions * mod_pow2(questions - 1);
total = (total + z + q) % MOD;
// Increment count of questions
questions += 1;
}
}
// Return the final count
return total;
}
// Given string S
let S = "?0?".split('');
// Function Call
document.write(inversions(S));
// This code is contributed by suresh07.
</script>
Producción:
3
Complejidad temporal: O(N)
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por koulick_sadhu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA