Los algoritmos de agrupamiento como el agrupamiento de K-means no realizan el agrupamiento de manera muy eficiente y es difícil procesar grandes conjuntos de datos con una cantidad limitada de recursos (como memoria o una CPU más lenta). Por lo tanto, los algoritmos de agrupamiento regulares no escalan bien en términos de tiempo de ejecución y calidad a medida que aumenta el tamaño del conjunto de datos. Aquí es donde entra en juego la agrupación en clústeres BIRCH. Agrupación y reducción iterativa equilibrada mediante jerarquías (BIRCH)es un algoritmo de agrupamiento que puede agrupar grandes conjuntos de datos generando primero un resumen pequeño y compacto del gran conjunto de datos que conserva la mayor cantidad de información posible. Este resumen más pequeño luego se agrupa en clústeres en lugar de agrupar el conjunto de datos más grande. BIRCH se utiliza a menudo para complementar otros algoritmos de agrupación mediante la creación de un resumen del conjunto de datos que ahora puede utilizar el otro algoritmo de agrupación. Sin embargo, BIRCH tiene un gran inconveniente: solo puede procesar atributos métricos. Un atributo métrico es cualquier atributo cuyos valores pueden representarse en el espacio euclidiano, es decir, no deben estar presentes atributos categóricos. Antes de implementar BIRCH, debemos comprender dos términos importantes: Función de agrupamiento (CF) y CF – Función de agrupamiento de árboles (CF):BIRCH resume grandes conjuntos de datos en regiones más pequeñas y densas denominadas entradas de función de agrupamiento (CF). Formalmente, una entrada de Característica de agrupación se define como un triple ordenado (N, LS, SS) donde ‘N’ es el número de puntos de datos en el grupo, ‘LS’ es la suma lineal de los puntos de datos y ‘SS’ es la suma al cuadrado de los puntos de datos en el grupo. Es posible que una entrada CF esté compuesta por otras entradas CF. Árbol CF: El árbol CF es la representación compacta real de la que hemos estado hablando hasta ahora. Un árbol CF es un árbol en el que cada Node hoja contiene un subclúster. Cada entrada en un árbol CF contiene un puntero a un Node secundario y una entrada CF formada por la suma de las entradas CF en los Nodes secundarios. Hay un número máximo de entradas en cada Node hoja. Este número máximo se llamaumbral _ Aprenderemos más sobre cuál es este valor de umbral. Parámetros del algoritmo BIRCH:
- umbral : el umbral es el número máximo de puntos de datos que puede contener un subclúster en el Node hoja del árbol CF.
- branching_factor : este parámetro especifica el número máximo de subclústeres de CF en cada Node (Node interno).
- n_clusters : el número de clústeres que se devolverán después de que se complete todo el algoritmo BIRCH, es decir, el número de clústeres después del último paso de agrupación. Si se establece en Ninguno, no se realiza el paso de agrupación final y se devuelven las agrupaciones intermedias.
Implementación de BIRCH en Python: por el bien de este ejemplo, generaremos un conjunto de datos para agrupar usando el método make_blobs() de scikit-learn. Para obtener más información sobre make_blobs(), puede consultar el siguiente enlace: https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_blobs.html Código: para crear 8 clústeres con 600 muestras generadas aleatoriamente y luego graficar los resultados en un diagrama de dispersión.
python3
# Import required libraries and modules import matplotlib.pyplot as plt from sklearn.datasets.samples_generator import make_blobs from sklearn.cluster import Birch # Generating 600 samples using make_blobs dataset, clusters = make_blobs(n_samples = 600, centers = 8, cluster_std = 0.75, random_state = 0) # Creating the BIRCH clustering model model = Birch(branching_factor = 50, n_clusters = None, threshold = 1.5) # Fit the data (Training) model.fit(dataset) # Predict the same data pred = model.predict(dataset) # Creating a scatter plot plt.scatter(dataset[:, 0], dataset[:, 1], c = pred, cmap = 'rainbow', alpha = 0.7, edgecolors = 'b') plt.show()
Gráfico de salida: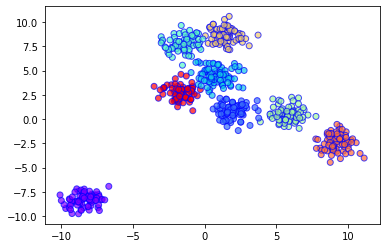
Publicación traducida automáticamente
Artículo escrito por alokesh985 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA