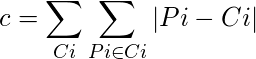ML | Clustering de K-Medoids con ejemplo resuelto

El algoritmo K-Medoids (también llamado partición alrededor de Medoid) fue propuesto en 1987 por Kaufman y Rousseeuw. Un medoid se puede definir como el punto en el grupo, cuyas diferencias con todos los demás puntos en el grupo es mínima.

La disimilitud de medoid(Ci) y object(Pi) se calcula usandoE = |Pi - Ci|

El costo en el algoritmo K-Medoids se da como

Algoritmo:

1. Inicializar: seleccione k puntos aleatorios de los n puntos de datos como medoids.
2. Asocie cada punto de datos al medoide más cercano utilizando cualquier método de métrica de distancia común.
3. Mientras el costo disminuye:
        Para cada medoide m, para cada dato o punto que no sea un medoide:
                1. Intercambie m y o, asocie cada punto de datos al medoide más cercano, vuelva a calcular el costo.
                2. Si el costo total es mayor que el del paso anterior, deshaga el intercambio.

Consideremos el siguiente ejemplo:

Si se dibuja un gráfico utilizando los puntos de datos anteriores, obtenemos lo siguiente:

Paso 1:
Deje que los 2 medoides seleccionados al azar, seleccione k = 2 y deje que C1 – (4, 5) y C2 – (8, 5) sean los dos medoides.

Paso 2: Cálculo del costo.
La disimilitud de cada punto no medoide con los medoides se calcula y tabula:

Cada punto se asigna al grupo de ese medoid cuya disimilitud es menor.
Los puntos 1, 2, 5van a cluster C1y 0, 3, 6, 7, 8van a cluster C2.
losCost = (3 + 4 + 4) + (3 + 1 + 1 + 2 + 2) = 20

Paso 3: seleccione aleatoriamente un punto no medoide y vuelva a calcular el costo.
Sea el punto elegido al azar (8, 4). La disimilitud de cada punto no medoide con los medoides, C1 (4, 5)y C2 (8, 4)se calcula y tabula.

Cada punto se asigna a ese grupo cuya disimilitud es menor. Entonces, los puntos 1, 2, 5van al clúster C1y 0, 3, 6, 7, 8van al clúster C2.
El New cost = (3 + 4 + 4) + (2 + 2 + 1 + 3 + 3) = 22
Costo de Intercambio = Costo Nuevo – Costo Anterior = 22 – 20 y 2 >0

Como el coste del swap no es inferior a cero, deshacemos el swap. Por lo tanto , (3, 4)y (7, 4)son los medoides finales. La agrupación sería de la siguiente manera

La complejidad del tiempo es .

ventajas:

1. Es simple de entender y fácil de implementar.
2. El algoritmo K-Medoid es rápido y converge en un número fijo de pasos.
3. PAM es menos sensible a los valores atípicos que otros algoritmos de partición.

Desventajas:

1. La principal desventaja de los algoritmos K-Medoid es que no es adecuado para agrupar grupos de objetos no esféricos (de forma arbitraria). Esto se debe a que se basa en minimizar las distancias entre los objetos no medoides y el medoide (el centro del cúmulo); brevemente, utiliza la compacidad como criterio de agrupamiento en lugar de la conectividad.
2. Puede obtener diferentes resultados para diferentes ejecuciones en el mismo conjunto de datos porque los primeros k medoids se eligen al azar.