ML | Agrupación difusa – Barcelona Geeks

Requisito previo: agrupamiento en aprendizaje automático

¿Qué es la agrupación?
La agrupación en clústeres es una técnica de aprendizaje automático no supervisada que divide los datos proporcionados en diferentes grupos en función de sus distancias (similitud) entre sí.

El algoritmo de agrupamiento de k-medias no supervisado da los valores de cualquier punto que se encuentra en un grupo particular como 0 o 1, es decir, verdadero o falso. Pero la lógica difusa da los valores borrosos de cualquier punto de datos en particular para estar en cualquiera de los grupos. Aquí, en el agrupamiento fuzzy c-means, encontramos el centroide de los puntos de datos y luego calculamos la distancia de cada punto de datos desde los centroides dados hasta que los grupos formados se vuelven constantes.

Suponga que los puntos de datos dados son {(1, 3), (2, 5), (6, 8), (7, 9)}

Los pasos para realizar el algoritmo son:

Paso 1: inicialice los puntos de datos en el número deseado de grupos al azar.
Supongamos que hay 2 grupos en los que se dividirán los datos, inicializando el punto de datos al azar. Cada punto de datos se encuentra en ambos grupos con algún valor de membresía que se puede asumir cualquier cosa en el estado inicial.

La siguiente tabla representa los valores de los puntos de datos junto con su pertenencia (gamma) en cada uno de los grupos.

Cluster    (1, 3)    (2, 5)    (4, 8)    (7, 9)
1)          0.8        0.7       0.2       0.1
2)          0.2        0.3       0.8       0.9

Paso 2: Encuentra el centroide.
La fórmula para encontrar el centroide (V) es:

$V_{ij} = ( \sum \limits_1^n ( \gamma_{ik}^m * x_k) / \sum \limits_1^n \gamma_{ik}^m$

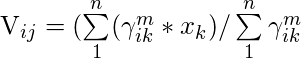
Donde µ es el valor de pertenencia borroso del punto de datos, m es el parámetro de borrosidad (generalmente tomado como 2) y xk es el punto de datos.
Aquí,

V11  = (0.82 *1 + 0.72 * 2 + 0.22 * 4 + 0.12 * 7) / ( (0.82 + 0.72  + 0.22  + 0.12 ) = 1.568
V12  = (0.82 *3 + 0.72 * 5 + 0.22 * 8 + 0.12 * 9) / ( (0.82 + 0.72  + 0.22  + 0.12 ) = 4.051
V11  = (0.22 *1 + 0.32 * 2 + 0.82 * 4 + 0.92 * 7) / ( (0.22 + 0.32  + 0.82  + 0.92 ) = 5.35
V11  = (0.22 *3 + 0.32 * 5 + 0.82 * 8 + 0.92 * 9) / ( (0.22 + 0.32  + 0.82  + 0.92 ) = 8.215

Centroids are: (1.568, 4.051) and (5.35, 8.215)

Paso 3: Averigüe la distancia de cada punto desde el centroide.

D11 = ((1 - 1.568)² + (3 - 4.051)²)^0.5 = 1.2
D12 = ((1 - 5.35)² + (3 - 8.215)²)^0.5 = 6.79

De manera similar, la distancia de todos los demás puntos se calcula a partir de ambos centroides.

Paso 4: Actualización de los valores de membresía.

$\gamma = \sum \limits_1^n {(d_{ki}^2 /d_{kj}^2)}^{1/m-1} ]^{-1}$

Para el punto 1, los nuevos valores de membresía son:

$\gamma_{11}$ = [{ [(1,2) ² / (1,2) ² ] + [(1,2) ² / (6,79) ² ]} ^ {(1 / (2 – 1))} ] ^-1 = 0,96

$\gamma_{12}$ = [{ [(6,79) ² / (6,79) ² ] + [(6,79) ² / (1,2) ² ]} ^ {(1 / (2 – 1))} ] ^-1 = 0,04
Alternativamente,
$\gamma_{12} = 1- \gamma_{11} = 0.04$

De manera similar, calcule todos los demás valores de pertenencia y actualice la array.

Paso 5: Repita los pasos (2-4) hasta que se obtengan los valores constantes para los valores de pertenencia o la diferencia sea menor que el valor de tolerancia (un valor pequeño hasta el cual se acepta la diferencia de valores de dos actualizaciones consecutivas).

Paso 6: Desfuzzificar los valores de membresía obtenidos.

Implementación: la biblioteca de aprendizaje fuzzy scikit tiene una función predefinida para fuzzy c-means que se puede usar en Python. Para usar fuzzy c-means necesita instalar la biblioteca skfuzzy .

pip install sklearn
pip install skfuzzy

Publicación traducida automáticamente

Artículo escrito por somya13 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta