ML | Agrupación espectral

Prerrequisitos: Clúster de K-Means

Spectral Clustering es un algoritmo de agrupamiento en crecimiento que ha funcionado mejor que muchos algoritmos de agrupamiento tradicionales en muchos casos. Trata cada punto de datos como un Node gráfico y, por lo tanto, transforma el problema de agrupamiento en un problema de partición de gráficos. Una implementación típica consta de tres pasos fundamentales: –

1. Construyendo el gráfico de similitud: este paso construye el gráfico de similitud en forma de una array de adyacencia que está representada por A. La array de adyacencia se puede construir de las siguientes maneras:-
   • Gráfico de vecindad de épsilon: Un parámetro épsilon se fija de antemano. Luego, cada punto está conectado a todos los puntos que se encuentran en su radio épsilon. Si todas las distancias entre dos puntos cualesquiera tienen una escala similar, normalmente los pesos de los bordes, es decir, la distancia entre los dos puntos, no se almacenan, ya que no proporcionan ninguna información adicional. Así, en este caso, el grafo construido es un grafo no dirigido y no ponderado.
   • K-vecinos más cercanos Un parámetro k se fija de antemano. Entonces, para dos vértices u y v, una arista se dirige de u a v solo si v está entre los k vecinos más cercanos de u. Tenga en cuenta que esto conduce a la formación de un gráfico ponderado y dirigido porque no siempre ocurre que para cada u que tiene v como uno de los k-vecinos más cercanos, será el mismo caso para v que tiene u entre sus k-más cercanos. vecinos Para hacer este gráfico no dirigido, se sigue uno de los siguientes enfoques:-
     1. Dirija una arista de u a v y de v a u si v está entre los k vecinos más cercanos de u O u está entre los k vecinos más cercanos de v.
     2. Dirija una arista de u a v y de v a u si v está entre los k vecinos más cercanos de u Y u está entre los k vecinos más cercanos de v.
   • Gráfico totalmente conectado: para construir este gráfico, cada punto está conectado con un borde no dirigido ponderado por la distancia entre los dos puntos a cualquier otro punto. Dado que este enfoque se utiliza para modelar las relaciones de vecindad local, normalmente se utiliza la métrica de similitud gaussiana para calcular la distancia.
2. Proyectar los datos en un espacio dimensional inferior: este paso se realiza para tener en cuenta la posibilidad de que los miembros del mismo grupo puedan estar muy lejos en el espacio dimensional dado. Por lo tanto, el espacio dimensional se reduce para que esos puntos estén más cerca en el espacio dimensional reducido y, por lo tanto, puedan agruparse mediante un algoritmo de agrupamiento tradicional. Se realiza calculando la Array Gráfica Laplaciana . Sin embargo, para calcularlo primero, se debe definir el grado de un Node. El grado del i-ésimo Node viene dado por

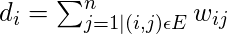
   Tenga en cuenta que 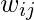es el borde entre los Nodes i y j como se define en la array de adyacencia anterior.

   La array de grados se define de la siguiente manera:

   

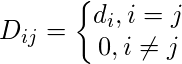
   Por lo tanto, la array gráfica laplaciana se define como: –

   

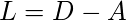
   Esta array luego se normaliza para la eficiencia matemática. Para reducir las dimensiones, primero se calculan los valores propios y los vectores propios respectivos. Si el número de conglomerados es k, entonces se toman los primeros valores propios y sus vectores propios y se apilan en una array tal que los vectores propios son las columnas.

3. Agrupación de datos: este proceso consiste principalmente en agrupar los datos reducidos mediante el uso de cualquier técnica de agrupamiento tradicional, generalmente agrupamiento de K-Means. Primero, a cada Node se le asigna una fila del normalizado de la Array Grafica Laplaciana. Luego, estos datos se agrupan utilizando cualquier técnica tradicional. Para transformar el resultado de la agrupación, se conserva el identificador de Node.

   Propiedades:

   1. Suposición sin menos: Esta técnica de agrupamiento, a diferencia de otras técnicas tradicionales, no asume que los datos sigan alguna propiedad. Por lo tanto, esto hace que esta técnica responda a una clase más genérica de problemas de agrupamiento.
   2. Facilidad de implementación y velocidad: este algoritmo es más fácil de implementar que otros algoritmos de agrupamiento y también es muy rápido, ya que consiste principalmente en cálculos matemáticos.
   3. No escalable: dado que implica la construcción de arrays y el cálculo de valores propios y vectores propios, requiere mucho tiempo para conjuntos de datos densos.

Los pasos a continuación demuestran cómo implementar Spectral Clustering usando Sklearn. Los datos para los siguientes pasos son los datos de la tarjeta de crédito que se pueden descargar desde Kaggle .

Paso 1: Importación de las bibliotecas requeridas

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import SpectralClustering
from sklearn.preprocessing import StandardScaler, normalize
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score

Paso 2: carga y limpieza de datos

# Changing the working location to the location of the data
cd "C:\Users\Dev\Desktop\Kaggle\Credit_Card"
  
# Loading the data
X = pd.read_csv('CC_GENERAL.csv')
  
# Dropping the CUST_ID column from the data
X = X.drop('CUST_ID', axis = 1)
  
# Handling the missing values if any
X.fillna(method ='ffill', inplace = True)
  
X.head()

Paso 3: preprocesamiento de los datos para que sean visibles

# Preprocessing the data to make it visualizable
  
# Scaling the Data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
  
# Normalizing the Data
X_normalized = normalize(X_scaled)
  
# Converting the numpy array into a pandas DataFrame
X_normalized = pd.DataFrame(X_normalized)
  
# Reducing the dimensions of the data
pca = PCA(n_components = 2)
X_principal = pca.fit_transform(X_normalized)
X_principal = pd.DataFrame(X_principal)
X_principal.columns = ['P1', 'P2']
  
X_principal.head()

Paso 4: construir los modelos de agrupamiento y visualizar el agrupamiento

En los pasos a continuación, dos modelos de agrupamiento espectral diferentes con diferentes valores para el parámetro ‘afinidad’. Puede leer sobre la documentación de la clase Spectral Clustering aquí .

a) afinidad = ‘rbf’

# Building the clustering model
spectral_model_rbf = SpectralClustering(n_clusters = 2, affinity ='rbf')
  
# Training the model and Storing the predicted cluster labels
labels_rbf = spectral_model_rbf.fit_predict(X_principal)

# Building the label to colour mapping
colours = {}
colours[0] = 'b'
colours[1] = 'y'
  
# Building the colour vector for each data point
cvec = [colours[label] for label in labels_rbf]
  
# Plotting the clustered scatter plot
  
b = plt.scatter(X_principal['P1'], X_principal['P2'], color ='b');
y = plt.scatter(X_principal['P1'], X_principal['P2'], color ='y');
  
plt.figure(figsize =(9, 9))
plt.scatter(X_principal['P1'], X_principal['P2'], c = cvec)
plt.legend((b, y), ('Label 0', 'Label 1'))
plt.show()

b) afinidad = ‘vecinos más cercanos’

# Building the clustering model
spectral_model_nn = SpectralClustering(n_clusters = 2, affinity ='nearest_neighbors')
  
# Training the model and Storing the predicted cluster labels
labels_nn = spectral_model_nn.fit_predict(X_principal)

Paso 5: Evaluación de las actuaciones

# List of different values of affinity
affinity = ['rbf', 'nearest-neighbours']
  
# List of Silhouette Scores
s_scores = []
  
# Evaluating the performance
s_scores.append(silhouette_score(X, labels_rbf))
s_scores.append(silhouette_score(X, labels_nn))
  
print(s_scores)

Paso 6: Comparación de las actuaciones

# Plotting a Bar Graph to compare the models
plt.bar(affinity, s_scores)
plt.xlabel('Affinity')
plt.ylabel('Silhouette Score')
plt.title('Comparison of different Clustering Models')
plt.show()