ML | Agrupación jerárquica (agrupación aglomerativa y divisiva)

En minería de datos y estadísticas, el análisis de conglomerados jerárquicos es un método de análisis de conglomerados que busca construir una jerarquía de conglomerados, es decir, una estructura de tipo árbol basada en la jerarquía. 

Básicamente, hay dos tipos de estrategias de análisis de conglomerados jerárquicos:

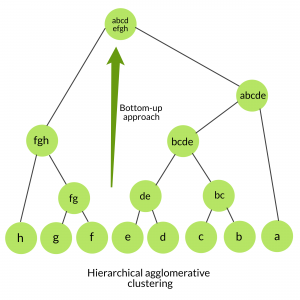
1. Clustering aglomerativo: también conocido como enfoque ascendente o clustering aglomerativo jerárquico (HAC). Una estructura que es más informativa que el conjunto de clústeres no estructurado devuelto por el agrupamiento plano. Este algoritmo de agrupamiento no requiere que especifiquemos previamente el número de agrupamientos. Los algoritmos ascendentes tratan cada dato como un clúster único desde el principio y luego aglomeran sucesivamente pares de clústeres hasta que todos los clústeres se fusionan en un único clúster que contiene todos los datos. 

Algoritmo: 

given a dataset (d1, d2, d3, ....dN) of size N
# compute the distance matrix
for i=1 to N:
   # as the distance matrix is symmetric about 
   # the primary diagonal so we compute only lower 
   # part of the primary diagonal 
   for j=1 to i:
      dis_mat[i][j] = distance[di, dj] 
each data point is a singleton cluster
repeat
   merge the two cluster having minimum distance
   update the distance matrix
until only a single cluster remains

Implementación de Python del algoritmo anterior usando la biblioteca scikit-learn: 

from sklearn.cluster import AgglomerativeClustering
import numpy as np
 
# randomly chosen dataset
X = np.array([[1, 2], [1, 4], [1, 0],
              [4, 2], [4, 4], [4, 0]])
 
# here we need to mention the number of clusters
# otherwise the result will be a single cluster
# containing all the data
clustering = AgglomerativeClustering(n_clusters = 2).fit(X)
 
# print the class labels
print(clustering.labels_)

Producción : 

[1, 1, 1, 0, 0, 0]

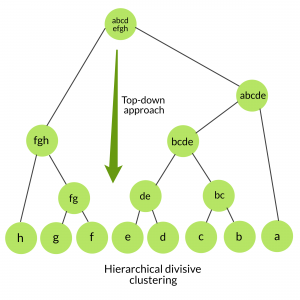
2. Agrupamiento divisivo: también conocido como enfoque de arriba hacia abajo. Este algoritmo tampoco requiere especificar previamente el número de clústeres. La agrupación en clústeres de arriba hacia abajo requiere un método para dividir un clúster que contenga todos los datos y proceda dividiendo los clústeres de forma recursiva hasta que los datos individuales se hayan dividido en clústeres únicos.

Algoritmo: 

given a dataset (d1, d2, d3, ....dN) of size N
at the top we have all data in one cluster
the cluster is split using a flat clustering method eg. K-Means etc
repeat
choose the best cluster among all the clusters to split
split that cluster by the flat clustering algorithm
until each data is in its own singleton cluster

Aglomeración jerárquica frente a agrupación divisiva: 

• El agrupamiento divisivo es más complejo en comparación con el agrupamiento aglomerativo, ya que en el caso del agrupamiento divisivo necesitamos un método de agrupamiento plano como «subrutina» para dividir cada grupo hasta que tengamos cada dato con su propio grupo único.
• El agrupamiento divisivo es más eficiente si no generamos una jerarquía completa hasta las hojas de datos individuales. La complejidad temporal de un agrupamiento aglomerativo ingenuo es O(n ³ ) porque escaneamos exhaustivamente la array N x N dist_mat para la distancia más baja en cada una de las N-1 iteraciones. Usando la estructura de datos de la cola de prioridad, podemos reducir esta complejidad a O(n ² logn) . Al usar algunas optimizaciones más, se puede reducir a O(n ² ) . Mientras que para el agrupamiento divisivo dado un número fijo de niveles superiores, utilizando un algoritmo plano eficiente como K-Means, los algoritmos divisivos son lineales en el número de patrones y grupos.
• Un algoritmo divisivo también es más preciso . El agrupamiento aglomerativo toma decisiones considerando los patrones locales o puntos vecinos sin tener inicialmente en cuenta la distribución global de datos. Estas decisiones tempranas no se pueden deshacer. mientras que el agrupamiento divisivo toma en consideración la distribución global de datos al tomar decisiones de partición de alto nivel.