Prerrequisitos: algoritmo a priori
Requisitos previos: Trie Estructura de datos
Los dos principales inconvenientes del algoritmo a priori son:
- En cada paso, se deben construir conjuntos de candidatos.
- Para construir los conjuntos de candidatos, el algoritmo tiene que escanear repetidamente la base de datos.
Estas dos propiedades inevitablemente hacen que el algoritmo sea más lento. Para superar estos pasos redundantes, se desarrolló un nuevo algoritmo de minería de reglas de asociación denominado Algoritmo de crecimiento de patrón frecuente. Supera las desventajas del algoritmo Apriori al almacenar todas las transacciones en una estructura de datos Trie. Considere los siguientes datos:-
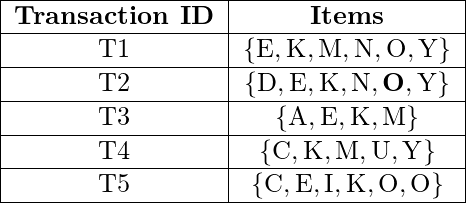
Los datos anteriores son un conjunto de datos hipotéticos de transacciones en las que cada letra representa un artículo. La frecuencia de cada elemento individual se calcula: –

Sea 3 el soporte mínimo. Se construye un conjunto de Patrones Frecuentes que contendrá todos los elementos cuya frecuencia sea mayor o igual al soporte mínimo. Estos elementos se almacenan en orden descendente de sus respectivas frecuencias. Después de la inserción de los elementos relevantes, el conjunto L se ve así:
L = {K : 5, E : 4, M : 3, O : 3, Y : 3}
Ahora, para cada transacción, se construye el respectivo conjunto de artículos pedidos . Se realiza iterando el conjunto de patrones frecuentes y verificando si el artículo actual está contenido en la transacción en cuestión. Si el artículo actual está contenido, el artículo se inserta en el conjunto de artículos pedidos para la transacción actual. La siguiente tabla se construye para todas las transacciones:

Ahora, todos los conjuntos de artículos pedidos se insertan en una estructura de datos Trie.
a) Insertando el conjunto {K, E, M, O, Y}:
Aquí, todos los elementos simplemente se vinculan uno tras otro en el orden de aparición en el conjunto e inicializan el recuento de soporte para cada elemento como 1.

b) Insertando el conjunto {K, E, O, Y}:
Hasta la inserción de los elementos K y E, simplemente la cuenta de soporte se incrementa en 1. Al insertar O podemos ver que no hay un vínculo directo entre E y O, por lo tanto, se inicializa un nuevo Node para el elemento O con la cuenta de soporte como 1 y el elemento E está vinculado a este nuevo Node. Al insertar Y, primero inicializamos un nuevo Node para el elemento Y con un recuento de soporte de 1 y vinculamos el nuevo Node de O con el nuevo Node de Y.

c) Insertando el conjunto {K, E, M}:
Aquí simplemente el recuento de soporte de cada elemento se incrementa en 1.

d) Insertando el conjunto {K, M, Y}:
De manera similar al paso b), primero se aumenta el recuento de soporte de K, luego se inicializan y vinculan nuevos Nodes para M e Y en consecuencia.

e) Insertando el conjunto {K, E, O}:
Aquí simplemente se aumentan los recuentos de apoyo de los elementos respectivos. Tenga en cuenta que el recuento de soporte del nuevo Node del elemento O aumenta.

Ahora, para cada elemento, se calcula la base del patrón condicional, que son las etiquetas de ruta de todas las rutas que conducen a cualquier Node del elemento dado en el árbol de patrones frecuentes. Tenga en cuenta que los elementos de la siguiente tabla están dispuestos en orden ascendente de frecuencia.

Ahora, para cada elemento, se construye el árbol de patrones frecuentes condicionales. Se realiza tomando el conjunto de elementos que es común en todas las rutas en la Base del patrón condicional de ese elemento y calculando su cuenta de soporte sumando las cuentas de soporte de todas las rutas en la Base del patrón condicional.

A partir del árbol de patrones frecuentes condicionales, las reglas de patrones frecuentes se generan emparejando los elementos del conjunto de árboles de patrones frecuentes condicionales con los correspondientes al elemento, como se indica en la siguiente tabla.

Para cada fila, se pueden inferir dos tipos de reglas de asociación, por ejemplo, para la primera fila que contiene el elemento, se pueden inferir las reglas K -> Y e Y -> K. Para determinar la regla válida, se calcula la confianza de ambas reglas y se retiene la que tiene una confianza mayor o igual que el valor mínimo de confianza.
Publicación traducida automáticamente
Artículo escrito por AlindGupta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA