Los datos del mundo real tienden a ser ruidosos. Los datos ruidosos son datos con una gran cantidad de información adicional sin sentido llamada ruido. Las rutinas de limpieza de datos (o limpieza de datos) intentan suavizar el ruido mientras identifican valores atípicos en los datos.
Hay tres técnicas de suavizado de datos de la siguiente manera:
- Agrupación: los métodos de agrupación suavizan un valor de datos ordenado consultando su «vecindario», es decir, los valores que lo rodean.
- Regresión: Conforma valores de datos a una función. La regresión lineal implica encontrar la «mejor» línea que se ajuste a dos atributos (o variables) para que un atributo pueda usarse para predecir el otro.
- Análisis de valores atípicos: los valores atípicos se pueden detectar mediante la agrupación, por ejemplo, cuando los valores similares se organizan en grupos o «conglomerados». Intuitivamente, los valores que quedan fuera del conjunto de conglomerados pueden considerarse atípicos.
Método de agrupamiento para el suavizado de datos:
aquí nos ocupamos del método de agrupamiento para el suavizado de datos. En este método, los datos se ordenan primero y luego los valores ordenados se distribuyen en varios cubos o contenedores . Como los métodos de agrupamiento consultan la vecindad de valores, realizan un suavizado local.
Básicamente, hay dos tipos de enfoques de agrupamiento:
- Binning de igual ancho (o distancia): el enfoque de binning más simple es dividir el rango de la variable en k intervalos de igual ancho. El ancho del intervalo es simplemente el rango [A, B] de la variable dividido por k,
w = (B-A) / k
Por lo tanto, el i -ésimo rango de intervalo será
[A + (i-1)w, A + iw]donde i = 1, 2, 3…..k
Este método no puede manejar bien los datos sesgados. - Agrupación de igual profundidad (o frecuencia): en la agrupación de igual frecuencia, dividimos el rango [A, B] de la variable en intervalos que contienen (aproximadamente) el mismo número de puntos; la misma frecuencia puede no ser posible debido a valores repetidos.
¿Cómo realizar el suavizado de los datos?
Hay tres enfoques para realizar el suavizado:
- Suavizado por medio de intervalo: En el suavizado por medio de intervalo, cada valor en un intervalo se reemplaza por el valor medio del intervalo.
- Suavizado por bin mediana: en este método, cada valor de bin se reemplaza por su valor de mediana bin.
- Suavizado por límite de bin: en el suavizado por límites de bin, los valores mínimo y máximo en un bin determinado se identifican como límites de bin. Luego, cada valor de intervalo se reemplaza por el valor de límite más cercano.
Datos ordenados por precio (en dólares): 2, 6, 7, 9, 13, 20, 21, 24, 30
Partition using equal frequency approach: Bin 1 : 2, 6, 7 Bin 2 : 9, 13, 20 Bin 3 : 21, 24, 30 Smoothing by bin mean : Bin 1 : 5, 5, 5 Bin 2 : 14, 14, 14 Bin 3 : 25, 25, 25 Smoothing by bin median : Bin 1 : 6, 6, 6 Bin 2 : 13, 13, 13 Bin 3 : 24, 24, 24 Smoothing by bin boundary : Bin 1 : 2, 7, 7 Bin 2 : 9, 9, 20 Bin 3 : 21, 21, 30
El binning también se puede utilizar como técnica de discretización . Aquí la discretización se refiere al proceso de convertir o dividir atributos, características o variables continuas en atributos/características/variables/intervalos discretos o nominales.
Por ejemplo, los valores de los atributos se pueden discretizar aplicando intervalos de igual ancho o igual frecuencia , y luego reemplazando cada valor de intervalo por la media o la mediana del intervalo, como en el suavizado por medias del intervalo o el suavizado por medianas del intervalo, respectivamente. Luego, los valores continuos se pueden convertir a un valor nominal o discretizado que es el mismo que el valor de su contenedor correspondiente.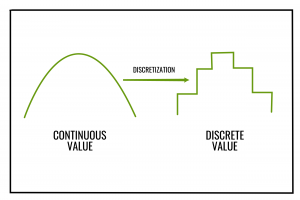
A continuación se muestra la implementación de Python:
bin_mean
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
# import statsmodels.api as sm
import statistics
import math
from collections import OrderedDict
x =[]
print("enter the data")
x = list(map(float, input().split()))
print("enter the number of bins")
bi = int(input())
# X_dict will store the data in sorted order
X_dict = OrderedDict()
# x_old will store the original data
x_old ={}
# x_new will store the data after binning
x_new ={}
for i in range(len(x)):
X_dict[i]= x[i]
x_old[i]= x[i]
x_dict = sorted(X_dict.items(), key = lambda x: x[1])
# list of lists(bins)
binn =[]
# a variable to find the mean of each bin
avrg = 0
i = 0
k = 0
num_of_data_in_each_bin = int(math.ceil(len(x)/bi))
# performing binning
for g, h in X_dict.items():
if(i<num_of_data_in_each_bin):
avrg = avrg + h
i = i + 1
elif(i == num_of_data_in_each_bin):
k = k + 1
i = 0
binn.append(round(avrg / num_of_data_in_each_bin, 3))
avrg = 0
avrg = avrg + h
i = i + 1
rem = len(x)% bi
if(rem == 0):
binn.append(round(avrg / num_of_data_in_each_bin, 3))
else:
binn.append(round(avrg / rem, 3))
# store the new value of each data
i = 0
j = 0
for g, h in X_dict.items():
if(i<num_of_data_in_each_bin):
x_new[g]= binn[j]
i = i + 1
else:
i = 0
j = j + 1
x_new[g]= binn[j]
i = i + 1
print("number of data in each bin")
print(math.ceil(len(x)/bi))
for i in range(0, len(x)):
print('index {2} old value {0} new value {1}'.format(x_old[i], x_new[i], i))
bin_median
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
# import statsmodels.api as sm
import statistics
import math
from collections import OrderedDict
x =[]
print("enter the data")
x = list(map(float, input().split()))
print("enter the number of bins")
bi = int(input())
# X_dict will store the data in sorted order
X_dict = OrderedDict()
# x_old will store the original data
x_old ={}
# x_new will store the data after binning
x_new ={}
for i in range(len(x)):
X_dict[i]= x[i]
x_old[i]= x[i]
x_dict = sorted(X_dict.items(), key = lambda x: x[1])
# list of lists(bins)
binn =[]
# a variable to find the mean of each bin
avrg =[]
i = 0
k = 0
num_of_data_in_each_bin = int(math.ceil(len(x)/bi))
# performing binning
for g, h in X_dict.items():
if(i<num_of_data_in_each_bin):
avrg.append(h)
i = i + 1
elif(i == num_of_data_in_each_bin):
k = k + 1
i = 0
binn.append(statistics.median(avrg))
avrg =[]
avrg.append(h)
i = i + 1
binn.append(statistics.median(avrg))
# store the new value of each data
i = 0
j = 0
for g, h in X_dict.items():
if(i<num_of_data_in_each_bin):
x_new[g]= round(binn[j], 3)
i = i + 1
else:
i = 0
j = j + 1
x_new[g]= round(binn[j], 3)
i = i + 1
print("number of data in each bin")
print(math.ceil(len(x)/bi))
for i in range(0, len(x)):
print('index {2} old value {0} new value {1}'.format(x_old[i], x_new[i], i))
bin_boundary
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
# import statsmodels.api as sm
import statistics
import math
from collections import OrderedDict
x =[]
print("enter the data")
x = list(map(float, input().split()))
print("enter the number of bins")
bi = int(input())
# X_dict will store the data in sorted order
X_dict = OrderedDict()
# x_old will store the original data
x_old ={}
# x_new will store the data after binning
x_new ={}
for i in range(len(x)):
X_dict[i]= x[i]
x_old[i]= x[i]
x_dict = sorted(X_dict.items(), key = lambda x: x[1])
# list of lists(bins)
binn =[]
# a variable to find the mean of each bin
avrg =[]
i = 0
k = 0
num_of_data_in_each_bin = int(math.ceil(len(x)/bi))
for g, h in X_dict.items():
if(i<num_of_data_in_each_bin):
avrg.append(h)
i = i + 1
elif(i == num_of_data_in_each_bin):
k = k + 1
i = 0
binn.append([min(avrg), max(avrg)])
avrg =[]
avrg.append(h)
i = i + 1
binn.append([min(avrg), max(avrg)])
i = 0
j = 0
for g, h in X_dict.items():
if(i<num_of_data_in_each_bin):
if(abs(h-binn[j][0]) >= abs(h-binn[j][1])):
x_new[g]= binn[j][1]
i = i + 1
else:
x_new[g]= binn[j][0]
i = i + 1
else:
i = 0
j = j + 1
if(abs(h-binn[j][0]) >= abs(h-binn[j][1])):
x_new[g]= binn[j][1]
else:
x_new[g]= binn[j][0]
i = i + 1
print("number of data in each bin")
print(math.ceil(len(x)/bi))
for i in range(0, len(x)):
print('index {2} old value {0} new value {1}'.format(x_old[i], x_new[i], i))
Referencia: https://en.wikipedia.org/wiki/Data_binning
Publicación traducida automáticamente
Artículo escrito por Debomit Dey y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA