ML | Descenso de gradiente estocástico (SGD)

Descenso de gradiente en resumen

Gradient Descent es un algoritmo de optimización genérico capaz de encontrar soluciones óptimas a una amplia gama de problemas.
La idea general es ajustar los parámetros iterativamente para minimizar la función de costo.
Un parámetro importante de Gradient Descent (GD) es el tamaño de los pasos, determinado por los hiperparámetros de tasa de aprendizaje. Si la tasa de aprendizaje es demasiado pequeña, el algoritmo tendrá que pasar por muchas iteraciones para converger, lo que llevará mucho tiempo, y si es demasiado alta, podemos saltar al valor óptimo.

Nota: Al usar Gradient Descent, debemos asegurarnos de que todas las características tengan una escala similar (p. ej., usando la clase StandardScaler de Scikit-Learn), o de lo contrario tardará mucho más en converger.

Tipos de descenso de gradiente:
por lo general, hay tres tipos de descenso de gradiente:

Descenso de gradiente por lotes
Descenso de gradiente estocástico
Descenso de gradiente de mini lotes

En este artículo, discutiremos el descenso de gradiente estocástico (SGD).

Descenso de gradiente estocástico (SGD):

La palabra ‘ estocástico ‘ significa un sistema o proceso vinculado con una probabilidad aleatoria. Por lo tanto, en Stochastic Gradient Descent, se seleccionan aleatoriamente algunas muestras en lugar de todo el conjunto de datos para cada iteración. En Gradient Descent, hay un término llamado «lote» que denota el número total de muestras de un conjunto de datos que se utiliza para calcular el gradiente para cada iteración. En la optimización típica de Gradient Descent, como Batch Gradient Descent, el lote se toma como el conjunto de datos completo. Aunque usar todo el conjunto de datos es realmente útil para llegar a los mínimos de una manera menos ruidosa y menos aleatoria, el problema surge cuando nuestro conjunto de datos crece.
Supongamos que tiene un millón de muestras en su conjunto de datos, por lo que si usa una técnica típica de optimización de descenso de gradiente, tendrá que usar el millón de muestras para completar una iteración mientras realiza el descenso de gradiente, y tiene que hacerse para cada iteración hasta alcanzar los mínimos. Por lo tanto, se vuelve computacionalmente muy costoso de realizar.
Este problema se resuelve mediante el Descenso de Gradiente Estocástico. En SGD, utiliza solo una sola muestra, es decir, un tamaño de lote de uno, para realizar cada iteración. La muestra se mezcla aleatoriamente y se selecciona para realizar la iteración.

Algoritmo SGD: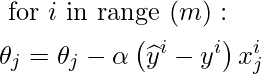
$\begin{aligned} &\text { for } i \text { in range }(m): \\ &\theta_{j}=\theta_{j}-\alpha\left(\widehat{y}^{i}-y^{i}\right) x_{j}^{i} \end{aligned}$
Entonces, en SGD, encontramos el gradiente de la función de costo de un solo ejemplo en cada iteración en lugar de la suma del gradiente de la función de costo de todos los ejemplos.

En SGD, dado que solo se elige aleatoriamente una muestra del conjunto de datos para cada iteración, la ruta que toma el algoritmo para alcanzar los mínimos suele ser más ruidosa que el típico algoritmo de descenso de gradiente. Pero eso no importa tanto porque no importa el camino que tome el algoritmo, siempre que lleguemos a los mínimos y con un tiempo de entrenamiento significativamente menor.

El camino tomado por Batch Gradient Descent –

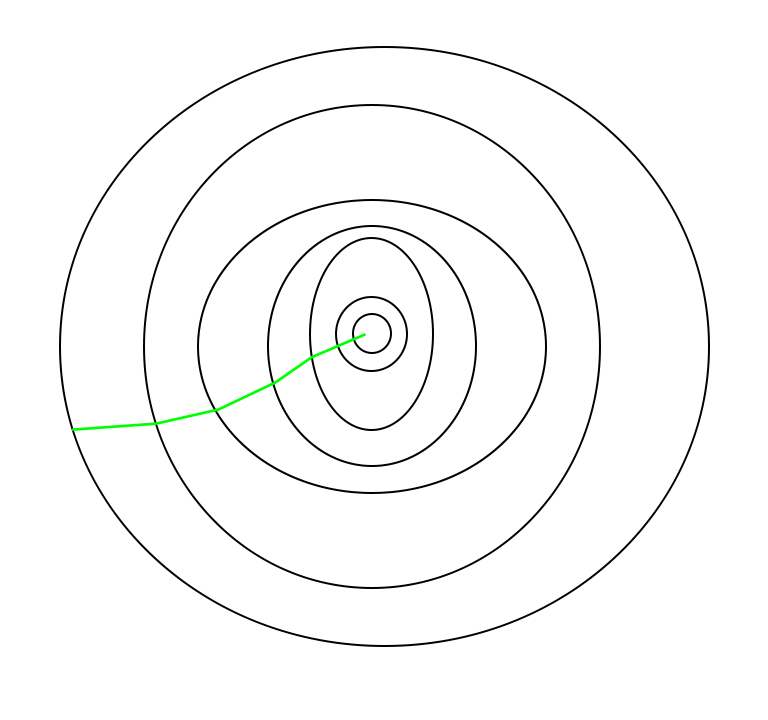
gd_path

Un camino ha sido tomado por Stochastic Gradient Descent –

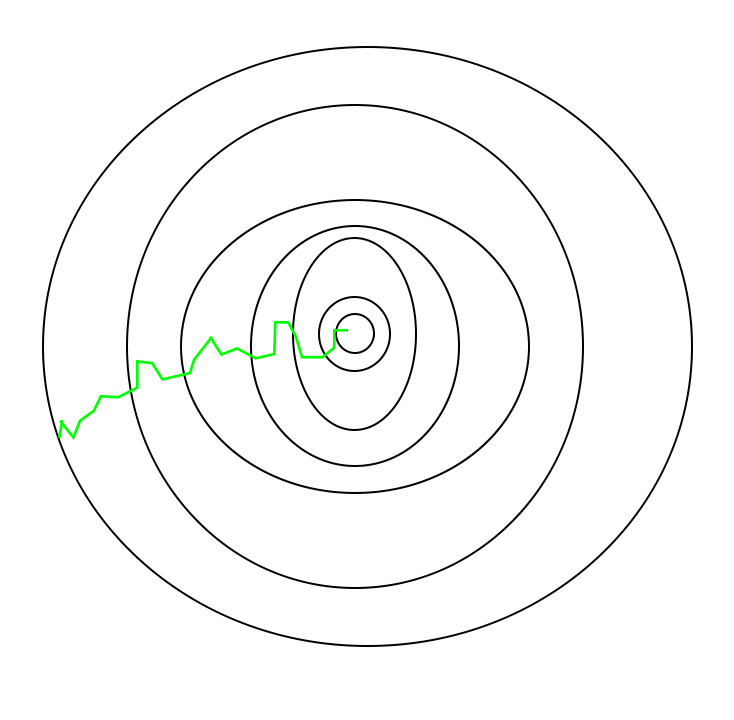
sgd_path

Una cosa a tener en cuenta es que, dado que SGD es generalmente más ruidoso que el descenso de gradiente típico, por lo general se necesita un mayor número de iteraciones para alcanzar los mínimos, debido a su aleatoriedad en su descenso. A pesar de que requiere una mayor cantidad de iteraciones para alcanzar los mínimos que el descenso de gradiente típico, todavía es computacionalmente mucho menos costoso que el descenso de gradiente típico. Por lo tanto, en la mayoría de los escenarios, se prefiere SGD a Batch Gradient Descent para optimizar un algoritmo de aprendizaje.

Pseudocódigo para SGD en Python:

Python3

def SGD(f, theta0, alpha, num_iters):
    """
       Arguments:
       f -- the function to optimize, it takes a single argument
            and yield two outputs, a cost and the gradient
            with respect to the arguments
       theta0 -- the initial point to start SGD from
       num_iters -- total iterations to run SGD for
       Return:
       theta -- the parameter value after SGD finishes
    """
    start_iter = 0
    theta = theta0
    for iter in xrange(start_iter + 1, num_iters + 1):
        _, grad = f(theta)
  
        # there is NO dot product ! return theta
        theta = theta - (alpha * grad)

Este ciclo de tomar los valores y ajustarlos en función de diferentes parámetros para reducir la función de pérdida se denomina retropropagación .

Publicación traducida automáticamente

Artículo escrito por Rahul_Roy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Descenso de gradiente estocástico (SGD):

Python3

Deja una respuesta Cancelar la respuesta