ML | Determinar el valor óptimo de K en K-Means Clustering

Requisito previo: Agrupación de K-Means | Introducción
Existe un método popular conocido como método del codo que se utiliza para determinar el valor óptimo de K para realizar el algoritmo de agrupación en clústeres de K-Means. La idea básica detrás de este método es que traza los distintos valores de costo con k cambiante . A medida que aumenta el valor de K , habrá menos elementos en el grupo. Entonces la distorsión promedio disminuirá. El menor número de elementos significa más cerca del centroide. Entonces, el punto donde más decae esta distorsión es el punto del codo .
 

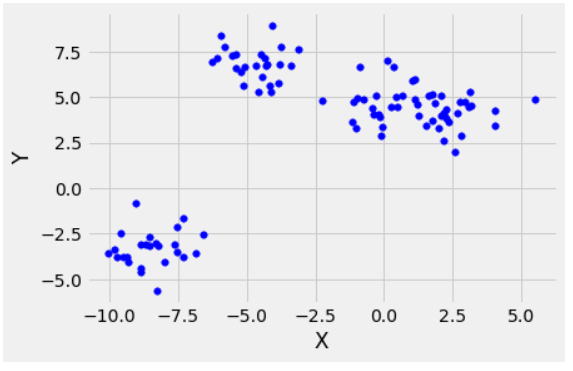
3 grupos se están formando

En la figura anterior, se observa claramente que la distribución de puntos está formando 3 grupos. Ahora, veamos la gráfica del error cuadrático (Costo) para diferentes valores de K. 
 

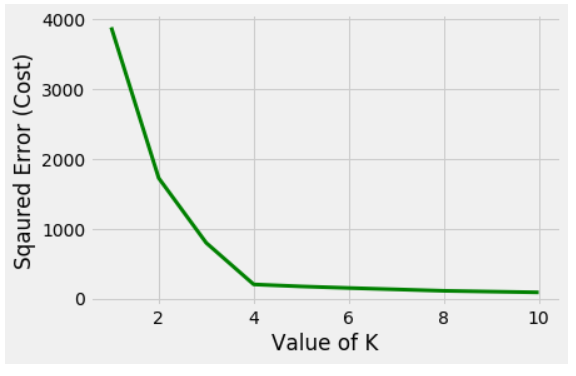
El codo se está formando en K=3

Claramente el codo se está formando en K=3. Entonces, el valor óptimo será 3 para realizar K-Means.
Otro ejemplo con 4 clústeres. 
 

4-clusters

Gráfico de costo correspondiente- 
 

El codo se está formando en K=4

En este caso el valor óptimo de k sería 4. (Observable desde los puntos dispersos).
A continuación se muestra la implementación de Python: 
 

import matplotlib.pyplot as plt
from matplotlib import style
from sklearn.cluster import KMeans
from sklearn.datasets.samples_generator import make_blobs
 
style.use("fivethirtyeight")
 
# make_blobs() is used to generate sample points
# around c centers (randomly chosen)
X, y = make_blobs(n_samples = 100, centers = 4,
                cluster_std = 1, n_features = 2)
                 
plt.scatter(X[:, 0], X[:, 1], s = 30, color ='b')
 
# label the axes
plt.xlabel('X')
plt.ylabel('Y')
 
plt.show()
plt.clf() # clear the figure

Producción: 
 

cost =[]
for i in range(1, 11):
    KM = KMeans(n_clusters = i, max_iter = 500)
    KM.fit(X)
     
    # calculates squared error
    # for the clustered points
    cost.append(KM.inertia_)    
 
# plot the cost against K values
plt.plot(range(1, 11), cost, color ='g', linewidth ='3')
plt.xlabel("Value of K")
plt.ylabel("Squared Error (Cost)")
plt.show() # clear the plot
 
# the point of the elbow is the
# most optimal value for choosing k

Producción: