Prerrequisito: Clúster de K-medias – Introducción
Inconveniente del algoritmo estándar de K-means:
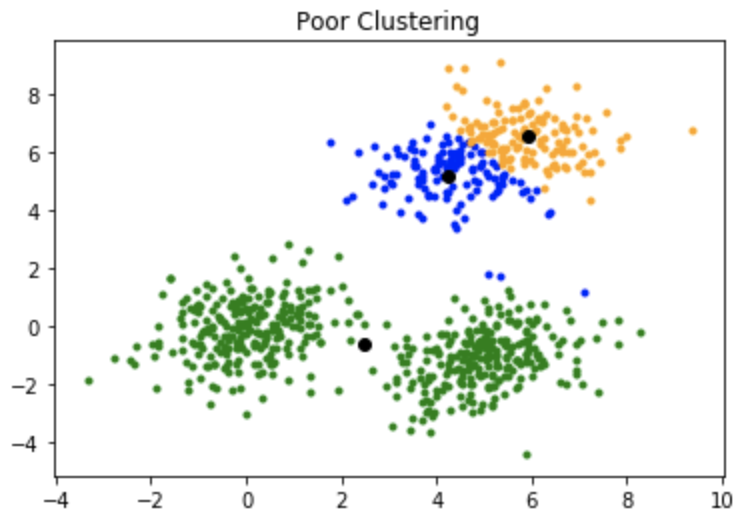
Una desventaja del algoritmo de K-medias es que es sensible a la inicialización de los centroides o los puntos medios. Entonces, si un centroide se inicializa para que sea un punto «lejano», podría terminar sin puntos asociados y, al mismo tiempo, más de un grupo podría terminar vinculado con un solo centroide. De manera similar, más de un centroide podría inicializarse en el mismo grupo, lo que resultaría en un agrupamiento deficiente. Por ejemplo, considere las imágenes que se muestran a continuación.
Una inicialización deficiente de los centroides resultó en un agrupamiento deficiente.
Así es como debería haber sido la agrupación:
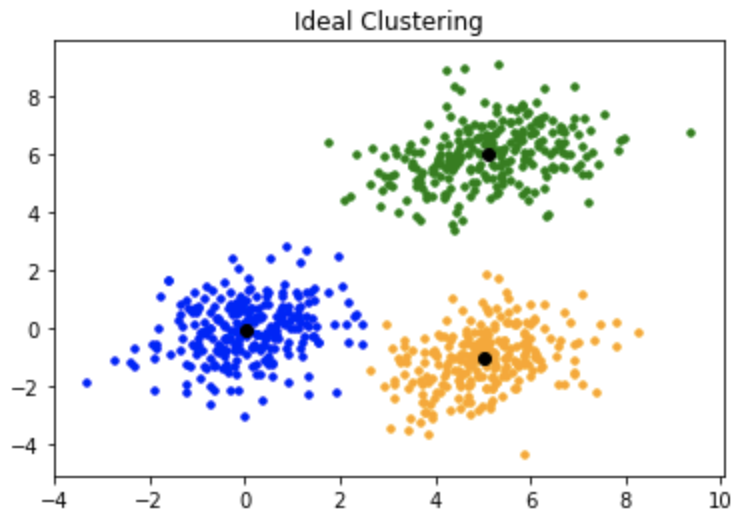
K-media++:
Para superar el inconveniente mencionado anteriormente, usamos K-means++. Este algoritmo asegura una inicialización más inteligente de los centroides y mejora la calidad del agrupamiento. Aparte de la inicialización, el resto del algoritmo es el mismo que el algoritmo estándar de K-means. Es decir, K-means++ es el algoritmo estándar de K-means junto con una inicialización más inteligente de los centroides.
Algoritmo de inicialización:
Los pasos involucrados son:
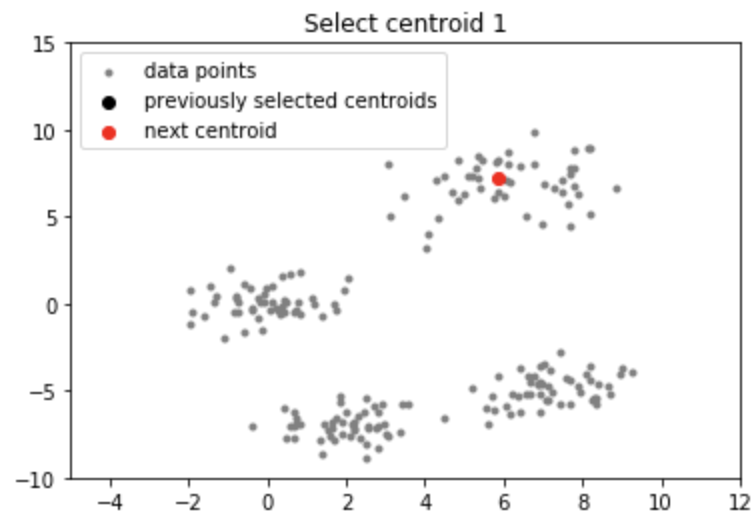
- Seleccione aleatoriamente el primer centroide de los puntos de datos.
- Para cada punto de datos, calcule su distancia desde el centroide elegido previamente más cercano.
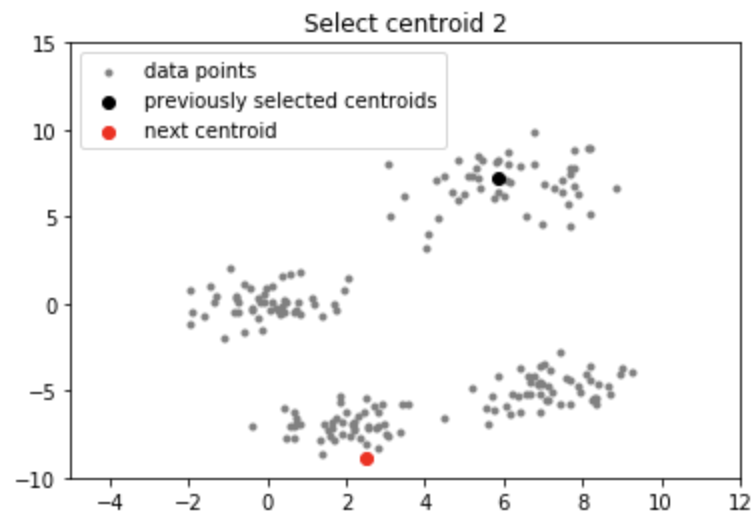
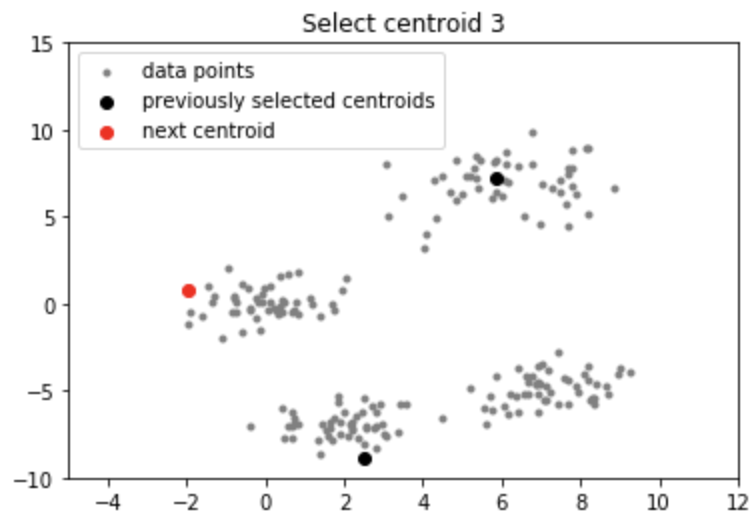
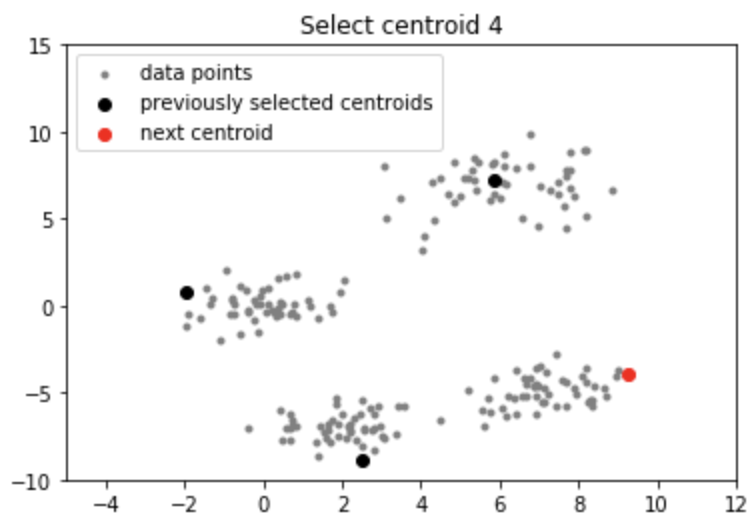
- Seleccione el siguiente centroide de los puntos de datos de modo que la probabilidad de elegir un punto como centroide sea directamente proporcional a su distancia desde el centroide más cercano elegido previamente. (es decir, el punto que tiene la distancia máxima desde el centroide más cercano es más probable que se seleccione a continuación como centroide)
- Repita los pasos 2 y 3 hasta que se hayan muestreado k centroides
Intuición:
Siguiendo el procedimiento anterior para la inicialización, seleccionamos los centroides que están alejados entre sí. Esto aumenta las posibilidades de recoger inicialmente centroides que se encuentran en diferentes grupos. Además, dado que los centroides se toman de los puntos de datos, cada centroide tiene algunos puntos de datos asociados al final.
Implementación:
Considere un conjunto de datos que tiene la siguiente distribución:
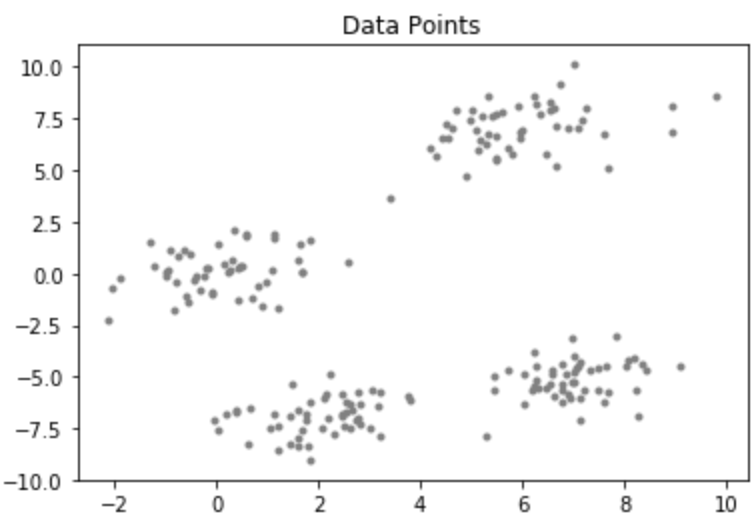
Código: código Python para el algoritmo KMean++
Python3
# importing dependencies
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sys
# creating data
mean_01 = np.array([0.0, 0.0])
cov_01 = np.array([[1, 0.3], [0.3, 1]])
dist_01 = np.random.multivariate_normal(mean_01, cov_01, 100)
mean_02 = np.array([6.0, 7.0])
cov_02 = np.array([[1.5, 0.3], [0.3, 1]])
dist_02 = np.random.multivariate_normal(mean_02, cov_02, 100)
mean_03 = np.array([7.0, -5.0])
cov_03 = np.array([[1.2, 0.5], [0.5, 1,3]])
dist_03 = np.random.multivariate_normal(mean_03, cov_01, 100)
mean_04 = np.array([2.0, -7.0])
cov_04 = np.array([[1.2, 0.5], [0.5, 1,3]])
dist_04 = np.random.multivariate_normal(mean_04, cov_01, 100)
data = np.vstack((dist_01, dist_02, dist_03, dist_04))
np.random.shuffle(data)
# function to plot the selected centroids
def plot(data, centroids):
plt.scatter(data[:, 0], data[:, 1], marker = '.',
color = 'gray', label = 'data points')
plt.scatter(centroids[:-1, 0], centroids[:-1, 1],
color = 'black', label = 'previously selected centroids')
plt.scatter(centroids[-1, 0], centroids[-1, 1],
color = 'red', label = 'next centroid')
plt.title('Select % d th centroid'%(centroids.shape[0]))
plt.legend()
plt.xlim(-5, 12)
plt.ylim(-10, 15)
plt.show()
# function to compute euclidean distance
def distance(p1, p2):
return np.sum((p1 - p2)**2)
# initialization algorithm
def initialize(data, k):
'''
initialized the centroids for K-means++
inputs:
data - numpy array of data points having shape (200, 2)
k - number of clusters
'''
## initialize the centroids list and add
## a randomly selected data point to the list
centroids = []
centroids.append(data[np.random.randint(
data.shape[0]), :])
plot(data, np.array(centroids))
## compute remaining k - 1 centroids
for c_id in range(k - 1):
## initialize a list to store distances of data
## points from nearest centroid
dist = []
for i in range(data.shape[0]):
point = data[i, :]
d = sys.maxsize
## compute distance of 'point' from each of the previously
## selected centroid and store the minimum distance
for j in range(len(centroids)):
temp_dist = distance(point, centroids[j])
d = min(d, temp_dist)
dist.append(d)
## select data point with maximum distance as our next centroid
dist = np.array(dist)
next_centroid = data[np.argmax(dist), :]
centroids.append(next_centroid)
dist = []
plot(data, np.array(centroids))
return centroids
# call the initialize function to get the centroids
centroids = initialize(data, k = 4)
Producción:
Nota: Aunque la inicialización en K-means++ es computacionalmente más costosa que el algoritmo estándar de K-means, el tiempo de ejecución para la convergencia al óptimo se reduce drásticamente para K-means++. Esto se debe a que es probable que los centroides que se eligen inicialmente ya se encuentren en diferentes grupos.
Publicación traducida automáticamente
Artículo escrito por savyakhosla y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA