Requisito previo: regresión lineal , R-cuadrado en regresión
¿Por qué? Prueba R cuadrada ajustada: la prueba
R cuadrada se usa para determinar la bondad de ajuste en el análisis de regresión. La bondad de ajuste implica cómo se ajusta mejor el modelo de regresión a los puntos de datos. Más es el valor de r-cuadrado cercano a 1, mejor es el modelo. Pero el problema radica en el hecho de que el valor de r-cuadrado siempre aumenta a medida que se agregan nuevas variables (atributos) al modelo, sin importar si los atributos recién agregados tienen un impacto positivo en el modelo o no. además, puede dar lugar a un sobreajuste del modelo si hay grandes no. de variables
El r-cuadrado ajustado es una forma modificada de r-cuadrado cuyo valor aumenta si los nuevos predictores tienden a mejorar el rendimiento del modelo y disminuye si los nuevos predictores no mejoran el rendimiento como se esperaba.
Para una mejor comprensión considerar:
Línea ajustada promedio
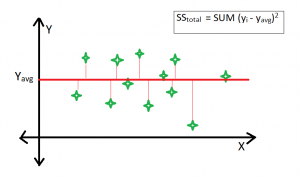
Línea mejor ajustada:

Fórmula R-cuadrado:
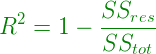
Claramente, SS tot siempre se fija para algunos puntos de datos si se agregan nuevos predictores al modelo, pero el valor de SS res disminuye a medida que el modelo intenta encontrar algunas correlaciones de los predictores agregados. Por lo tanto, el valor de r-cuadrado siempre aumenta.
R-cuadrado ajustado:

Cuadrado R ajustado
Aquí, k es el no. de regresores y n es el tamaño de la muestra.
si la variable recién agregada es lo suficientemente buena como para mejorar el rendimiento del modelo, superará la disminución debida a k . De lo contrario, un aumento en k disminuirá el valor de r-cuadrado ajustado.
Ejemplo-
Caso 1:
Python3
import pandas as pd
import numpy as np
# Download dataset and add complete path of the dataset.
# Importing dataset
s = pd.read_csv('Salary_Data.csv')
# Used to standardise statsmodel in python
f = np.ones((30, 1))
s.insert(0, 'extra', f)
# Gives summary of data model->gives value of r-square and adjusted r-square
import statsmodels.formula.api as sm
X_opt = s.iloc[:, :-1]
Y1 = s.iloc[:, -1]
regressor_OLS = sm.OLS(endog = Y1, exog = X_opt).fit()
regressor_OLS.summary()
Producción :

Tabla de resumen
Caso #2:
Python3
import pandas as pd
import numpy as np
# Download dataset and add complete path of the dataset.
# Importing dataset
s = pd.read_csv('Salary_Data.csv')
# Used to standarise statsmodel in python
f = np.ones((30, 1))
s.insert(0, 'extra', f)
# Inserting a new column to dataset having employee ids
g =[]
for i in range(1, 31):
g.append(i)
s.insert(2, 'Id', g)
# Gives summary of data model->gives value of r-square and adjusted r-square
import statsmodels.formula.api as sm
X_opt = s.iloc[:, :-1]
Y1 = s.iloc[:, -1]
regressor_OLS = sm.OLS(endog = Y1, exog = X_opt).fit()
regressor_OLS.summary()
Producción :

Tabla de resumen
Explicación:
valor de R-cuadrado y valor de r-cuadrado ajustado 0,957, 0,955 respectivamente. Pero cuando se agrega un atributo Id, que es un atributo irrelevante, da r-square y r-square ajustado igual a 0.958, 0.954 respectivamente.
Por lo tanto, al agregar un atributo irrelevante en el conjunto de datos, el valor de r-cuadrado aumenta (de 0,957 a 0,958). Pero el valor del cuadrado r ajustado disminuye (de 0,955 a 0,954).
Publicación traducida automáticamente
Artículo escrito por deepak_jain y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA