Modelado de lenguaje N-Gram con NLTK

El modelado del lenguaje es la forma de determinar la probabilidad de cualquier secuencia de palabras. El modelado del lenguaje se utiliza en una amplia variedad de aplicaciones, como el reconocimiento de voz, el filtrado de spam, etc. De hecho, el modelado del lenguaje es el objetivo clave detrás de la implementación de muchos modelos de procesamiento del lenguaje natural de última generación.

Métodos de modelado del lenguaje:

Dos tipos de modelado del lenguaje:

Modelado estadístico del lenguaje : el modelado estadístico del lenguaje, o modelado del lenguaje, es el desarrollo de modelos probabilísticos que pueden predecir la siguiente palabra en la secuencia dadas las palabras que la preceden. Ejemplos como el modelado del lenguaje N-gram.
Modelado de lenguaje neuronal : los métodos de redes neuronales están logrando mejores resultados que los métodos clásicos tanto en modelos de lenguaje independientes como cuando los modelos se incorporan a modelos más grandes en tareas desafiantes como el reconocimiento de voz y la traducción automática. Una forma de realizar un modelo de lenguaje neuronal es a través de incrustaciones de palabras.

N-grama

N-grama se puede definir como la secuencia contigua de n elementos de una muestra dada de texto o habla. Los elementos pueden ser letras, palabras o pares de bases según la aplicación. Los N-gramas generalmente se recopilan a partir de un corpus de texto o voz (un conjunto de datos de texto largo).

Modelo de lenguaje N-grama:

Un modelo de lenguaje N-grama predice la probabilidad de un N-grama dado dentro de cualquier secuencia de palabras en el idioma. Un buen modelo de N-grama puede predecir la siguiente palabra en la oración, es decir, el valor de p(w|h)

Ejemplo de N-grama como unigrama («Este», «artículo», «es», «en», «PNL») o bi-grama (‘Este artículo’, ‘el artículo es’, ‘está en’, ‘ en PNL’).

Ahora, estableceremos una relación sobre cómo encontrar la siguiente palabra en la oración usando

. Necesitamos calcular p(w|h), donde está el candidato para la siguiente palabra. Por ejemplo, en el ejemplo anterior, consideremos, queremos calcular cuál es la probabilidad de que la última palabra sea «PNL» dadas las palabras anteriores:

$p(NLP | this\, article\, is\, on)$

Después de generalizar la ecuación anterior se puede calcular como:

$p(w_5 | w_1, w_2, w_3, w_4) \, or \, P(W)$

$= p(w_n | w_1, w_2...w_n)$

Pero, ¿cómo lo calculamos? La respuesta está en la regla de la string de probabilidad:

$P(A|B) = \frac{P(A,B)}{P(B)}\\ P(A,B) = P(A|B)P(B)\\$

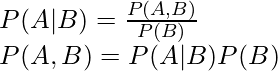
Ahora generaliza la ecuación anterior:

$P(X_1,X_2, ...,X_n) = P(X_1) P(X_2 | X_1) P(X_3 | X_1, X_2) .... P(X_n | X_1, X_2,...X_n)\\ P(w_1 w_2 w_3 ...w_n) =\prod_i P(w_i | w_1 w_2 ... w_n)$

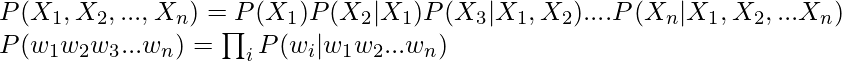
Simplificando la fórmula anterior utilizando los supuestos de Markov:

$P(w_i | w_1, w_2, ...w_{i-1}) \approx P(w_i | w_{i-k},... w_{i-1} )$

Para unigrama:

$P(w_1 w_2, ... w_n) \approx \prod_i P(w_i)$

Para bigrama:

$P(w_i | w_1 w_2, ..w_{i-1}) \approx P(w_i | w_{i-1})$

Implementación

Python3

# imports
import string
import random
import nltk
nltk.download('punkt')
nltk.download('stopwords')
nltk.download('reuters')
from nltk.corpus import reuters
from nltk import FreqDist
 
# input the reuters sentences
sents  =reuters.sents()
 
# write the removal characters such as : Stopwords and punctuation
stop_words = set(stopwords.words('english'))
string.punctuation = string.punctuation +'"'+'"'+'-'+'''+'''+'—'
string.punctuation
removal_list = list(stop_words) + list(string.punctuation)+ ['lt','rt']
removal_list
 
# generate unigrams bigrams trigrams
unigram=[]
bigram=[]
trigram=[]
tokenized_text=[]
for sentence in sents:
  sentence = list(map(lambda x:x.lower(),sentence))
  for word in sentence:
        if word== '.':
            sentence.remove(word)
        else:
            unigram.append(word)
   
  tokenized_text.append(sentence)
  bigram.extend(list(ngrams(sentence, 2,pad_left=True, pad_right=True)))
  trigram.extend(list(ngrams(sentence, 3, pad_left=True, pad_right=True)))
 
# remove the n-grams with removable words
def remove_stopwords(x):    
    y = []
    for pair in x:
        count = 0
        for word in pair:
            if word in removal_list:
                count = count or 0
            else:
                count = count or 1
        if (count==1):
            y.append(pair)
    return (y)
unigram = remove_stopwords(unigram)
bigram = remove_stopwords(bigram)
trigram = remove_stopwords(trigram)
 
# generate frequency of n-grams
freq_bi = FreqDist(bigram)
freq_tri = FreqDist(trigram)
 
d = defaultdict(Counter)
for a, b, c in freq_tri:
    if(a != None and b!= None and c!= None):
      d[a, b] += freq_tri[a, b, c]
       
 
# Next word prediction     
s=''
def pick_word(counter):
    "Chooses a random element."
    return random.choice(list(counter.elements()))
prefix = "he", "said"
print(" ".join(prefix))
s = " ".join(prefix)
for i in range(19):
    suffix = pick_word(d[prefix])
    s=s+' '+suffix
    print(s)
    prefix = prefix[1], suffix

he said
he said kotc
he said kotc made
he said kotc made profits
he said kotc made profits of
he said kotc made profits of 265
he said kotc made profits of 265 ,
he said kotc made profits of 265 , 457
he said kotc made profits of 265 , 457 vs
he said kotc made profits of 265 , 457 vs loss
he said kotc made profits of 265 , 457 vs loss eight
he said kotc made profits of 265 , 457 vs loss eight cts
he said kotc made profits of 265 , 457 vs loss eight cts net
he said kotc made profits of 265 , 457 vs loss eight cts net loss
he said kotc made profits of 265 , 457 vs loss eight cts net loss 343
he said kotc made profits of 265 , 457 vs loss eight cts net loss 343 ,
he said kotc made profits of 265 , 457 vs loss eight cts net loss 343 , 266
he said kotc made profits of 265 , 457 vs loss eight cts net loss 343 , 266 ,
he said kotc made profits of 265 , 457 vs loss eight cts net loss 343 , 266 , 000
he said kotc made profits of 265 , 457 vs loss eight cts net loss 343 , 266 , 000 shares

Métricas para modelos de lenguaje

Entropía : Entropía, como medida de la cantidad de información transmitida por Claude Shannon. A continuación se muestra la fórmula para representar la entropía.

$H(p) = \sum_{x} p(x)\cdot (-log(p(x)))\\$

H(p) siempre es mayor que igual a 0.

Entropía cruzada : mide la capacidad del modelo entrenado para representar datos de prueba ( $W_{1}^{i-1}$ ).

$H(p) =\sum_{i=1}^{x} \frac{1}{n} (-log_2(p(w_i | w_{1}^{i-1})))$

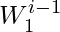La entropía cruzada siempre es mayor o igual que la entropía, es decir, la incertidumbre del modelo no puede ser menor que la incertidumbre real.

Perplejidad : la perplejidad es una medida de qué tan bien una distribución de probabilidad predice una muestra. Puede entenderse como una medida de incertidumbre. La perplejidad se puede calcular por entropía cruzada al exponente de 2.

$2^{Cross-Entropy}$

A continuación se presenta la fórmula para el cálculo de la Probabilidad del conjunto de prueba asignada por el modelo de lenguaje, normalizada por el número de palabras:

$PP(W) = \sqrt[n]{\prod_{i=1}^{N}\frac{1}{P(w_i | w_{i-1})}}$

Por ejemplo:

Tomemos un ejemplo de la oración: ‘Procesamiento del lenguaje natural’. Para predecir la primera palabra, digamos que la palabra tiene las siguientes probabilidades:

palabra	P(palabra \| <inicio>)
los	0.4
Procesando	0.3
Natural	0.12
Idioma	0.18

Ahora, conocemos la probabilidad de obtener la primera palabra como natural. Pero, ¿cuál es la probabilidad de obtener la siguiente palabra después de obtener la palabra ‘ Lenguaje ‘ después de la palabra ‘ Natural ‘?

palabra	P(palabra \| ‘Natural’ )
los	0.05
Procesando	0.3
Natural	0.15
Idioma	0.5

Después de obtener la probabilidad de generar palabras ‘Lenguaje natural’, ¿cuál es la probabilidad de obtener ‘ Procesamiento ‘?

palabra	P(palabra \| ‘Idioma’ )
los	0.1
Procesando	0.7
Natural	0.1
Idioma	0.1

Ahora, la perplejidad se puede calcular como:

$PP(W) = \sqrt[n]{\prod_{i=1}^{N}\frac{1}{P(w_i | w_{i-1})}} = \sqrt[3]{\frac{1}{0.12 * 0.5 * 0.7}} \approx 2.876$

A partir de eso también podemos calcular la entropía:

*** QuickLaTeX cannot compile formula:
 

*** Error message:
Error: Nothing to show, formula is empty

Deficiencias:

Para obtener un mejor contexto del texto, necesitamos valores más altos de n, pero esto también aumentará la sobrecarga computacional.
El valor creciente de n en n-gram también puede conducir a la escasez.

Referencias

Modelado del lenguaje N-gram Diapositivas de Stanford

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Implementación

Python3

Métricas para modelos de lenguaje

Deficiencias:

Referencias

Deja una respuesta Cancelar la respuesta