Supongamos que hay un conjunto de puntos de datos que deben agruparse en varias partes o grupos en función de su similitud. En el aprendizaje automático, esto se conoce como agrupamiento.
Hay varios métodos disponibles para la agrupación como:
- K significa agrupamiento
- Agrupación jerárquica
- Modelos de mezcla gaussiana
En este artículo, se discutirá el modelo de mezcla gaussiana.
Distribución normal o gaussiana
En la vida real, muchos conjuntos de datos se pueden modelar mediante distribución gaussiana (univariante o multivariante). Por lo tanto, es bastante natural e intuitivo suponer que los grupos provienen de diferentes distribuciones gaussianas. O dicho de otro modo, se intenta modelar el conjunto de datos como una mezcla de varias Distribuciones Gaussianas. Esta es la idea central de este modelo.
En una dimensión, la función de densidad de probabilidad de una distribución gaussiana viene dada por
![]()
where ![]() and
and ![]() are respectively mean and variance of the distribution.
are respectively mean and variance of the distribution.
For Multivariate ( let us say d-variate) Gaussian Distribution, the probability density function is given by
![]()
Here ![]() is a d dimensional vector denoting the mean of the distribution and
is a d dimensional vector denoting the mean of the distribution and ![]() is the d X d covariance matrix.
is the d X d covariance matrix.
Modelo de mezcla gaussiana
Supongamos que hay K conglomerados (en aras de la simplicidad aquí se supone que se conoce el número de conglomerados y es K). Así ![]() y
y ![]() también se estima para cada k. Si hubiera sido una sola distribución, se habrían estimado por el método de máxima verosimilitud . Pero dado que hay K tales grupos y la densidad de probabilidad se define como una función lineal de las densidades de todas estas K distribuciones, es decir
también se estima para cada k. Si hubiera sido una sola distribución, se habrían estimado por el método de máxima verosimilitud . Pero dado que hay K tales grupos y la densidad de probabilidad se define como una función lineal de las densidades de todas estas K distribuciones, es decir
![]()
donde ![]() es el coeficiente de mezcla para la k-ésima distribución.
es el coeficiente de mezcla para la k-ésima distribución.
Para estimar los parámetros por el método de máxima probabilidad logarítmica, calcule p(X| ![]() ,
, ![]() ,
, ![]() ).
).
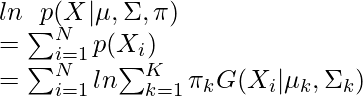
Ahora defina una variable aleatoria ![]() tal que
tal que ![]() =p(k|X).
=p(k|X).
Del teorema de Bayes,

Ahora, para que la función de verosimilitud logarítmica sea máxima, su derivada de ![]() con respecto a
con respecto a ![]() ,
, ![]() y
y ![]() debe ser cero. Igualando la derivada de
debe ser cero. Igualando la derivada de ![]() con respecto
con respecto ![]() a cero y reordenando los términos,
a cero y reordenando los términos,
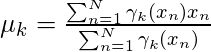
Del mismo modo, tomando la derivada con respecto a ![]() y pi respectivamente, se pueden obtener las siguientes expresiones.
y pi respectivamente, se pueden obtener las siguientes expresiones.
![]()
And ![]()
Nota: ![]() denota el número total de puntos de muestra en el grupo k-ésimo. Aquí se supone que hay un número total de N de muestras y cada muestra que contiene d características se denota por
denota el número total de puntos de muestra en el grupo k-ésimo. Aquí se supone que hay un número total de N de muestras y cada muestra que contiene d características se denota por ![]() .
.
Entonces se puede ver claramente que los parámetros no se pueden estimar en forma cerrada. Aquí es donde el algoritmo de maximización de expectativas es beneficioso.
Algoritmo de maximización de expectativas (EM)
El algoritmo Expectation-Maximization (EM) es una forma iterativa de encontrar estimaciones de máxima verosimilitud para los parámetros del modelo cuando los datos están incompletos o tienen algunos puntos de datos faltantes o tienen algunas variables ocultas. EM elige algunos valores aleatorios para los puntos de datos faltantes y estima un nuevo conjunto de datos. Estos nuevos valores luego se usan recursivamente para estimar una mejor primera cita, completando los puntos que faltan, hasta que los valores se fijan.
Estos son los dos pasos básicos del algoritmo EM, a saber, Paso E o Paso de expectativa o Paso de estimación y Paso M o Paso de maximización .
- Paso de estimación:
- initialize
 ,
, 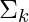 y
y 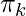 por algunos valores aleatorios, o por K significa resultados de agrupamiento o por resultados de agrupamiento jerárquico.
por algunos valores aleatorios, o por K significa resultados de agrupamiento o por resultados de agrupamiento jerárquico. - Luego, para esos valores de parámetros dados, estime el valor de las variables latentes (es decir,
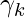 )
)
- initialize
- Paso de maximización:
- Actualice el valor de los parámetros (es decir
 ,
, 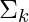 y
y 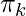 ) calculados utilizando el método ML.
) calculados utilizando el método ML.
- Actualice el valor de los parámetros (es decir
Algoritmo:
- Inicializar la media
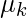 [Tex],[/Tex]
[Tex],[/Tex] 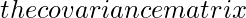 [Tex]\Sigma_k[/Tex]
[Tex]\Sigma_k[/Tex] 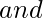
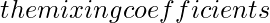 [Tex]\pi_k[/Tex]
[Tex]\pi_k[/Tex]
*** QuickLaTeX no puede compilar la fórmula: *** Mensaje de error: Error: nada que mostrar, la fórmula está vacía

- Calcule los
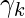 valores de [Tex] para todos los k. [/Tex]
valores de [Tex] para todos los k. [/Tex] 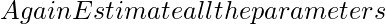
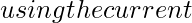 [Tex]\gamma_k[/Tex]
[Tex]\gamma_k[/Tex]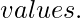
- Calcule la función de log-verosimilitud.
- Pon algún criterio de convergencia
- Si el valor de log-verosimilitud converge a algún valor (o si todos los parámetros convergen a algún valor), entonces deténgase , de lo contrario regrese al Paso 2 .
*** QuickLaTeX cannot compile formula: *** Error message: Error: Nothing to show, formula is empty
Ejemplo: En este ejemplo, se toma el conjunto de datos IRIS . En Python, hay una clase GaussianMixture para implementar GMM.
Nota: es posible que este código no se ejecute en un compilador en línea. Utilice un ide fuera de línea.
- Cargue el conjunto de datos de iris desde el paquete de conjuntos de datos. Para simplificar las cosas, tome las únicas dos primeras columnas (es decir, longitud y ancho del sépalo, respectivamente).
- Ahora trace el conjunto de datos.
Python3
import numpy as np import pandas as pd import matplotlib.pyplot as plt from pandas import DataFrame from sklearn import datasets from sklearn.mixture import GaussianMixture # load the iris dataset iris = datasets.load_iris() # select first two columns X = iris.data[:, :2] # turn it into a dataframe d = pd.DataFrame(X) # plot the data plt.scatter(d[0], d[1])
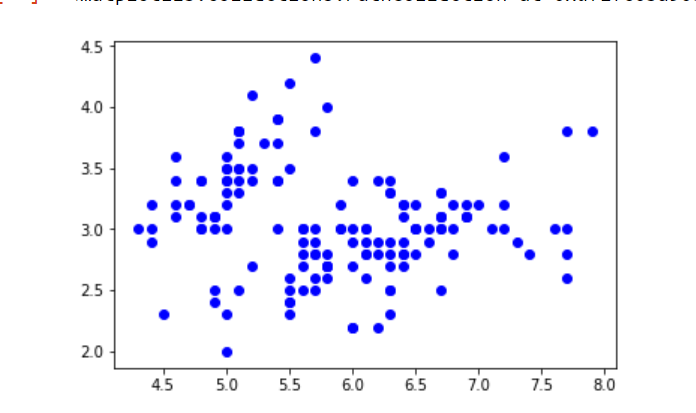
- Ahora ajusta los datos como una mezcla de 3 gaussianas.
- Luego haga el agrupamiento, es decir, asigne una etiqueta a cada observación. Además, encuentre el número de iteraciones necesarias para que la función de verosimilitud logarítmica converja y el valor de verosimilitud logarítmica convergente.
Python3
gmm = GaussianMixture(n_components = 3) # Fit the GMM model for the dataset # which expresses the dataset as a # mixture of 3 Gaussian Distribution gmm.fit(d) # Assign a label to each sample labels = gmm.predict(d) d['labels']= labels d0 = d[d['labels']== 0] d1 = d[d['labels']== 1] d2 = d[d['labels']== 2] # plot three clusters in same plot plt.scatter(d0[0], d0[1], c ='r') plt.scatter(d1[0], d1[1], c ='yellow') plt.scatter(d2[0], d2[1], c ='g')
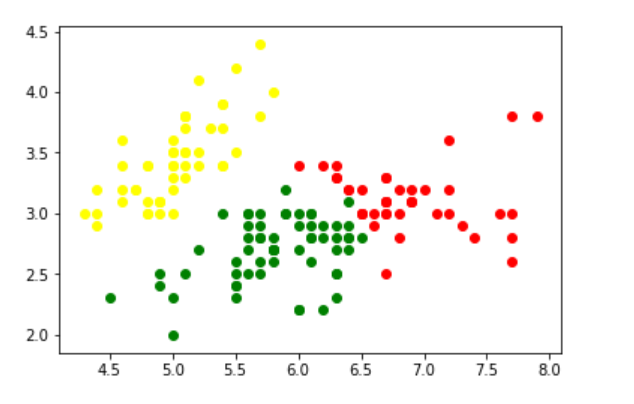
- Imprima el valor de verosimilitud logarítmica convergente y no. de iteraciones necesarias para que el modelo converja
Python3
# print the converged log-likelihood value print(gmm.lower_bound_) # print the number of iterations needed # for the log-likelihood value to converge print(gmm.n_iter_)</div>

- Por lo tanto, se necesitaron 7 iteraciones para que el logaritmo de verosimilitud convergiera. Si se realizan más iteraciones, no se puede observar ningún cambio apreciable en el valor de probabilidad logarítmica.
Publicación traducida automáticamente
Artículo escrito por tufan_gupta2000 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA