Modelo Erdos Renyl (para generar gráficos aleatorios)

En la teoría de grafos, el modelo de Erdos-Rényi es cualquiera de los dos modelos estrechamente relacionados para generar gráficos aleatorios.

Hay dos variantes estrechamente relacionadas del modelo de gráfico aleatorio Erdos-Rényi (ER).

En el modelo G(n, M), se elige un gráfico uniformemente al azar de la colección de todos los gráficos que tienen n Nodes y M aristas. Por ejemplo, en el modelo G(3, 2), cada uno de los tres gráficos posibles en tres vértices y dos aristas se incluyen con probabilidad 1/3.

En el modelo G(n, p), se construye un gráfico conectando Nodes aleatoriamente. Cada arista se incluye en el gráfico con probabilidad p independiente de cualquier otra arista. De manera equivalente, todos los gráficos con n Nodes y M aristas tienen la misma probabilidad de $p^M (1-p)^\binom{n}{2}-M$

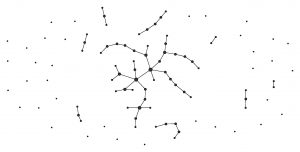
Erdos Renyl Model for generating Random Graphs 1

Un gráfico generado por el modelo binomial de Erdos y Rényi (p = 0,01)

El parámetro p en este modelo se puede considerar como una función de ponderación; a medida que p aumenta de 0 a 1, es cada vez más probable que el modelo incluya gráficos con más bordes y cada vez menos probable que incluya gráficos con menos bordes. En particular, el caso p = 0.5 corresponde al caso donde todos los $2^{\binom{n}{2}}$ gráficos en n vértices se eligen con igual probabilidad.

El artículo tratará básicamente del modelo G (n,p) donde n es el número de Nodes a crear y p define la probabilidad de unión de cada Node con el otro.

Propiedades de G(n, p)

Con la notación anterior, un gráfico en G(n, p) tiene ${\binom{n}{2}}p$ aristas en promedio. La distribución del grado de cualquier vértice en particular es binomial:

$P(deg(v)=k)=\binom{n-1}{k}{p^k}{1-p^{n-1-k}}$

Donde n es el número total de vértices en el gráfico.

Dado $P(deg(v)=k)\rightarrow\frac{{np^k}{e^{-np}}}{k!}$ que as $n\rightarrow infinity$ y np= constante Esta distribución es de Poisson para n grande y np = const. En un artículo de 1960, Erdos y Rényi describieron el comportamiento de G(n, p) con mucha precisión para varios valores de p. Sus resultados incluyeron que:

Si np < 1, entonces un gráfico en G(n, p) seguramente no tendrá componentes conectados de tamaño mayor que O(log(n)).
Si np = 1, entonces un gráfico en G(n, p) casi seguramente tendrá un componente más grande cuyo tamaño es del orden de $n^{2/3}$ .
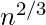Si np 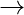$\rightarrow$ c > 1, donde c es una constante, entonces un gráfico en G(n, p) casi seguramente tendrá un componente gigante único que contiene una fracción positiva de los vértices. Ningún otro componente contendrá más de O(log(n)) vértices.
Si 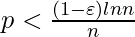$p<\frac{(1-\varepsilon )ln n}{n}$ , entonces un gráfico en G(n, p) casi seguramente contendrá vértices aislados y, por lo tanto, será desconectado.
Si 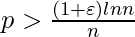$p>\frac{(1+\varepsilon )ln n}{n}$ , entonces un gráfico en G(n, p) casi seguramente será conexo.

Por lo tanto $\frac{ln n}{n}$ , es un umbral definido para la conectividad de G(n, p). Otras propiedades del gráfico se pueden describir casi con precisión cuando n tiende a infinito. Por ejemplo, hay ak(n) (aproximadamente igual a 2log2(n)) tal que la camarilla más grande en G(n, 0.5) tiene casi con certeza un tamaño k(n) o k(n) + 1. Por lo tanto, incluso aunque encontrar el tamaño de la camarilla más grande en un gráfico es NP-completo, el tamaño de la camarilla más grande en un gráfico «típico» (según este modelo) se entiende muy bien. Curiosamente, los gráficos de bordes duales de los gráficos Erdos-Renyi son gráficos con casi la misma distribución de grados, pero con correlaciones de grados y un coeficiente de agrupamiento significativamente más alto.

A continuación, describiré el código que se usará para hacer el gráfico ER. Para la implementación del código a continuación, deberá instalar la biblioteca netwrokx y también deberá instalar la biblioteca matplotlib. A continuación, verá el código exacto del gráfico que se ha utilizado como una función de la biblioteca networkx últimamente en este artículo.

Erdos_renyi_graph(n, p, seed=Ninguno, dirigido=Falso)

Devuelve un gráfico aleatorio G(n,p), también conocido como gráfico de Erdos-Rényi o gráfico binomial.
El modelo G(n,p) elige cada una de las posibles aristas con probabilidad p. Las funciones binomial_graph() y erdos_renyi_graph() son alias de esta función.

Parámetros: n (int) – El número de Nodes.
p (flotante): probabilidad de creación de borde.
semilla (int, opcional): semilla para el generador de números aleatorios (predeterminado = ninguno).
dirigida (bool, opcional (predeterminado=Falso)): si es verdadera, esta función devuelve un gráfico dirigido.

Python

#importing the networkx library
>>> import networkx as nx
 
#importing the matplotlib library for plotting the graph
>>> import matplotlib.pyplot as plt
 
>>> G= nx.erdos_renyi_graph(50,0.5)
>>> nx.draw(G, with_labels=True)
>>> plt.show()

Erdos Renyl Model for generating Random Graphs 2

Figura 1: Para n=50, p=0,5

El ejemplo anterior es para 50 Nodes y, por lo tanto, no está claro.

Al considerar el caso de un número menor de Nodes (por ejemplo, 10), puede ver claramente la diferencia.

Usando los códigos para varias probabilidades, podemos ver la diferencia fácilmente:

Python

>>> I= nx.erdos_renyi_graph(10,0)
>>> nx.draw(I, with_labels=True)
>>> plt.show()

Erdos Renyl Model for generating Random Graphs 3

Figura 2: Para n=10, p=0

Python

>>> K=nx.erdos_renyi_graph(10,0.25)
>>> nx.draw(K, with_labels=True)
>>> plt.show()

Erdos Renyl Model for generating Random Graphs 4

Figura 3: Para n=10, p=0,25

Python

>>>H= nx.erdos_renyi_graph(10,0.5)
>>> nx.draw(H, with_labels=True)
>>> plt.show()

Erdos Renyl Model for generating Random Graphs 5

Figura 4: Para n=10, p=0,5

Este algoritmo se ejecuta en $n^2$ tiempo O( ). Para gráficos dispersos (es decir, para valores pequeños de p), fast_gnp_random_graph() es un algoritmo más rápido. Por lo tanto, los ejemplos anteriores definen claramente el uso del modelo erdos renyi para hacer gráficos aleatorios y cómo usar lo anterior usando la biblioteca networkx de python. A continuación, analizaremos el gráfico de ego y varios otros tipos de gráficos en python utilizando la biblioteca networkx.

. Este artículo es una contribución de Jayant Bisht . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Python

Python

Python

Python

Deja una respuesta Cancelar la respuesta