Modelo de Phong (reflexión especular) en gráficos por computadora

Requisito previo: modelos de iluminación básicos

Modelo de reflexión de Phong:
cuando observamos superficies brillantes iluminadas, como superficies brillantes, láminas de metal pulidas, manzanas, etc., encontramos una especie de punto brillante en ciertas ubicaciones de puntos de observación. Este fenómeno se llama reflexión especular.

Observa la siguiente figura:
 

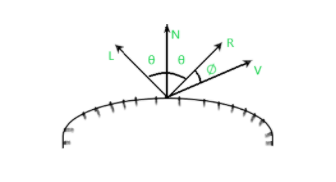
N = Normal vector
L = Point light source
V = Viewing direction
R = is representing the unit vector directed towards the ideal specular reflection
∅ = Viewing angle relative to the specular reflection direction R.
θ = Angle made by L & R with N.

Para superficies reflectoras ideales (espejo perfecto), la luz incidente se refleja solo en la dirección de reflexión especular. Entonces, en este caso, podríamos ver la luz reflejada cuando los vectores V y R coinciden (ángulo de visión (∅ = 0)) .

Una superficie brillante tiene un rango de reflexión especular estrecho, mientras que una superficie opaca tiene un rango de reflexión más amplio. Un modelo empírico para calcular el rango de reflexión especular, inventado por Phong Bui Tuong, también se conoce como modelo de reflexión especular de Phong . Este modelo establece la intensidad de la reflexión especular directamente proporcional al cos ^{n _s} (∅) . El rango del ángulo ∅ puede estar entre 0 ≤ ∅ ≤ 1. Donde n _s es un parámetro de reflexión especular cuyo valor está determinado por el tipo de superficie a mostrar. El valor de n _spara superficies más brillantes (brillantes) podría ser 100 o más, mientras que para superficies opacas su valor es 1 o menos de 1. La intensidad de la reflexión especular depende de las propiedades del objeto (Material) de la superficie y el ángulo de incidencia de la luz, así como otros factores como la polarización y el color de la luz incidente.

Podemos controlar la variación de la intensidad de la luz a través de la reflexión especular utilizando la función de reflexión espectral W(∅) para cada superficie. Donde ∅ el valor se encuentra en el rango de 0 ≤ ∅ ≤ 1. En general W(∅) tiende a aumentar a medida que aumenta el ángulo de incidencia, en ∅=90* W(90*)=1, y en este caso, todos la luz que incide sobre la superficie del material se refleja. Entonces, usando la función de reflexión espectral W(∅) podemos escribir el modelo de reflexión especular de Phong como: 

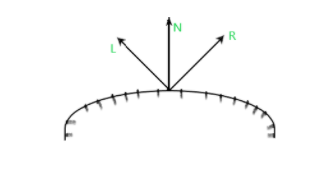
Para muchas superficies de materiales opacos, los reflejos especulares son casi constantes para todos los ángulos de incidencia. Entonces, en tal caso, podemos reemplazar W(∅) con un coeficiente constante (Ks) , y el valor se encuentra entre 0 y 1, para cada superficie:

Since, V & R are unit vectors so, |V|=|R|=1 :
                          V * R = |V|*|R|*cos(θ)  , 
                          V * R = cos(θ)                                                                                 

Entonces, podemos escribir la ecuación anterior como:

Aquí, R se puede calcular mediante la proyección de L en la dirección del vector normal:

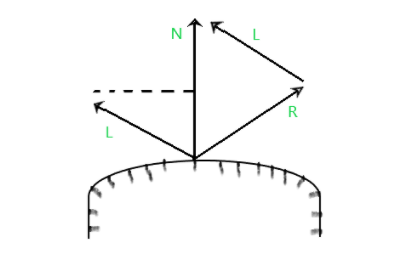
R + L = (2*N.L)*N
So, using the above equation specular-reflection vector is obtained,
R = (2*N.L)*N - L.

Las reflexiones ambientales, difusas y especulares combinadas en el modelo de Phong se pueden representar como la siguiente ecuación con múltiples fuentes de luz:

Entonces, para una fuente de luz de un solo punto, podemos modelar los reflejos combinados y especulares desde un punto en una superficie iluminada como:

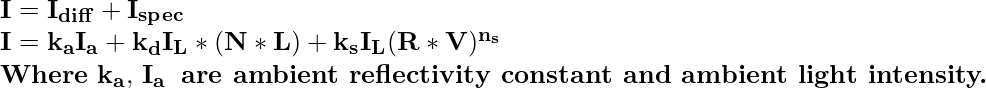
Y, para una fuente de luz de n puntos, la ecuación será: