Moore – Pseudoinversa de Penrose | Matemáticas

En álgebra lineal, la pseudoinversa ( $A^{+}$ ) de una array A es una generalización de la array inversa. El uso más común de la pseudoinversa es calcular la solución que mejor se ajusta a un sistema de ecuaciones lineales que carece de una solución única. La inversa de Moore-Penrose es el tipo más conocido de array pseudoinversa. El término inversa generalizada se usa a veces como sinónimo de pseudoinverso.

Sea el sistema dado como:
$\overrightarrow{y} = A\overrightarrow{x}$

Conocemos A y $\overrightarrow{y}$ , y queremos encontrar $\overrightarrow{x}$ .
Donde:
$\overrightarrow{x}$ y $\overrightarrow{y}$ son vectores,
A es una array

Si A es una array cuadrada, se procede de la siguiente manera:
$\overrightarrow{y} = A\overrightarrow{x}$

$A^{-1}\overrightarrow{y} = A^{-1}A\overrightarrow{x}$

$A^{-1}\overrightarrow{y} = I\overrightarrow{x}$

$A^{-1}\overrightarrow{y} = \overrightarrow{x}$

Pero si A no es una array cuadrada, no podemos calcular el $A^{-1}$ . Sin embargo, podemos formar la pseudoinversa.
$A^{+}\equiv pseudoinverse$

Si vamos en detalle al sistema ie $\overrightarrow{y} = A\overrightarrow{x}$ , entonces representa el siguiente conjunto de ecuaciones:
$a_1_, _1 x_1 + a_1_, _2 x_2 + . . . + a_1_, _n x_n = y_1$

$a_2_, _1 x_1 + a_2_, _2 x_2 + . . . + a_2_, _n x_n = y_2$
. .
. .
. .
$a_m_, _1 x_1 + a_m_, _2 x_2 + . . . + a_m_, _n x_n = y_m$

que también se puede escribir en forma matricial como sigue: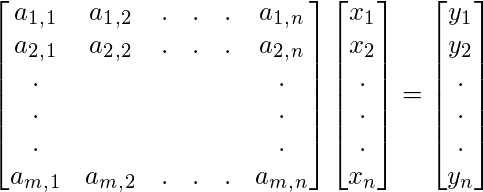
$\begin{bmatrix} a_1_, _1 & a_1_, _2&.&.&.&a_1_, _n \\ a_2_, _1 & a_2_, _2 &.&.&.&a_2_, _n\\ . & & & & & . \\ . & & & & & . \\ . & & & & & . \\ a_m_, _1 & a_m_, _2 &.&.&.&a_m_, _n\\ \end{bmatrix} % \begin{bmatrix} x_1\\ x_2\\ .\\ .\\ .\\ x_n\\ \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ .\\ .\\ .\\ y_n\\ \end{bmatrix}$

Donde m > n , lo que significa que el número de filas es mayor que el número de columnas o el número de filas es mayor que el número de variables.

Solución al problema anterior:
Hay varias formas de resolver el problema anterior. Una solución implica Moore – Penrose Pseudoinverse. Escribimos la pseudoinversa de Moore-Penrose como $A^[+}$ .
Tenemos $A^{+}A = I$ pero $AA^{+} \neq I$ a menos que A tenga el inverso habitual.
Entonces, para resolver el problema procedemos de la siguiente manera:
$\overrightarrow{y} = A\overrightarrow{x}$

$A^{+}\overrightarrow{y} \approx A^{+}A\overrightarrow{x}$

$A^{+}\overrightarrow{y} \approx I\overrightarrow{x}$

$A^{+}\overrightarrow{y} \approx \overrightarrow{x}$

Así de simple resolvemos las ecuaciones lineales usando la pseudoinversa de Moore – Penrose. La derivación de la pseudoinversa de Moore-Penrose está más allá del alcance de este artículo. Puedes pasar por este enlace por si quieres saber más al respecto. Aquí, simplemente se presenta el método para calcularlo. La pseudoinversa de Moore-Penrose se calcula como
$A^{+} = (A^{T} A)^{-1} A^{T}$

Ejemplo:

Consider below 3 linear equations: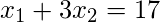






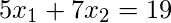
Equivalently we can write above equations in matrix form as shown below:





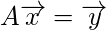
After we compute the Moore - Penrose pseudoinverse using , we will get:



Check the matrix product  you will get identity matrix I.


We have,


Then,





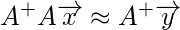
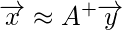
After you compute above computation, you will get the final answer as

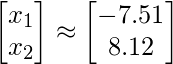
Nota: La pseudoinversa de Moore – Penrose resuelve el problema en el sentido del error de mínimos cuadrados. En general, no existe una solución exacta para los problemas sobredeterminados. Entonces, si verifica la solución, no obtendrá la y requerida exacta, sino un valor aproximado de y.

Publicación traducida automáticamente

Artículo escrito por mkumarchaudhary06 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta