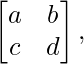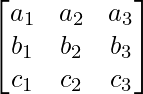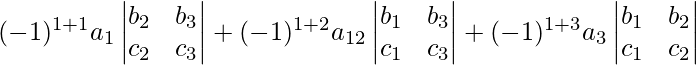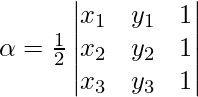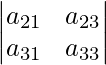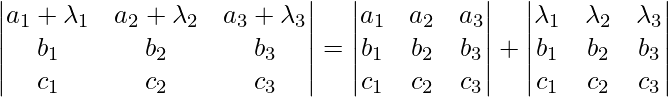El último destino de la escuela: clase 12. Si deseas ingresar a la universidad de tus sueños, esta es la clase en la que debes obtener la mejor puntuación para obtener un viaje al destino de tu futura carrera. Especialmente cuando no encuentra notas para materias como Matemáticas y Ciencias que aterrorizan a los estudiantes cuando se trata de prepararse para el examen de la junta. Es por eso que, para facilitar su búsqueda, GeeksforGeeks seleccionó las notas de matemáticas de clase 12 de CBSE, guiadas por expertos.
Nuestras notas de matemáticas de la clase 12 de CBSE están escritas en un lenguaje sencillo y cubren casi todos los capítulos del plan de estudios de matemáticas de la clase 12 de CBSE. Prepararse a partir de estas notas de revisión de matemáticas de la clase 12 de CBSE ayudará a los estudiantes a lograr altas calificaciones en su grado 12, así como exámenes exitosos como JEE Mains y JEE Advanced.
Estas notas provistas por GeeksforGeeks ayudarán a los estudiantes a comprender cada concepto y revisar a fondo antes de las pruebas.
Estas notas fueron escritas por expertos en el contenido y tienen la gran ventaja de que los estudiantes estarán bien preparados para responder algún tipo de pregunta que se pueda hacer en los exámenes.
El plan de estudios de matemáticas de clase 12 de CBSE cubre todos los capítulos importantes que figuran en los libros de texto NCERT revisados que incluyen algunos temas importantes de matemáticas de clase 10 como funciones compuestas , arrays y sus tipos , ecuación de tangentes y normales , etc.
Para mejorar los conceptos básicos de los estudiantes, GeeksforGeeks también cubrió más de 1500 preguntas más frecuentes de matemáticas , fórmulas importantes por capítulos y muchas más basadas en el nuevo plan de estudios Class 12th CBSE. Estas notas y otros materiales de estudio ayudan a los estudiantes a prepararse para los exámenes de la Junta.

Capítulo 1: Relaciones y Funciones
El término ‘relación’ en matemáticas se deriva de la definición de relación del idioma inglés, que establece que dos objetos o cantidades están vinculados si existe una conexión o relación observable entre ellos. Este Capítulo 1 de Clase 12 puede ser muy confuso, por lo tanto, los estudiantes pueden incluso usar las estrategias para mejorar su aprendizaje.
Veamos las Notas del Capítulo 1 de Matemáticas de Clase 12. Capítulo 1 – Relación y funciones discuten la introducción de relaciones y funciones , tipos de relaciones, tipos de funciones , la composición de funciones y funciones invertibles , y operaciones binarias .
Fórmulas importantes cubiertas en CBSE Clase 12 Capítulo 1- Relaciones y funciones,
- Relación : una relación vacía R en X, se puede definir como: R = φ ⊂ X × X
- Una relación de equivalencia R en X se define como una relación que puede representar los tres tipos de relaciones: relaciones reflexivas, simétricas y transitivas.
- Relación simétrica R en X: (a, b) ∈ R ⇒ (b, a) ∈ R.
- Relación reflexiva R en X: (a, a) ∈ R, ∀ a ∈ X.
- Relación transitiva R en X: (a, b) ∈ R y (b, c) ∈ R, ⇒ (a, c) ∈ R .
- Mientras que, la relación Universal R en X: R = X × X .
- Función- Dependiendo de la conclusión obtenida, las funciones f: X → Y pueden ser de diferentes tipos como,
- Uno-uno o función inyectiva : Si f(x 1 ) = f(x 2 ) ⇒ x 1 = x 2 ∀ x 1 , x 2 ∈ X.
- Función sobreyectiva o sobreyectiva : Si y ∈ Y, ∃ x ∈ X tal que f(x) = y.
- Función uno-uno y sobre o biyectiva : si f sigue tanto las propiedades uno como sobre.
- Función invertible: Si ∃ g: Y → X tal que gof = I X y fog = I Y . Esto puede suceder solo si f es uno-uno y sobre.
El capítulo 1 de CBSE Class 12 Math Notes cubre los siguientes temas:
- Tipos de funciones
- Funciones compuestas
- Funciones invertibles
- Composición de Funciones
- Funciones inversas
- Verificación de funciones inversas por composición
Más recursos para CBSE Clase 12 Matemáticas Capítulo 1
- Clase 12 Soluciones NCERT Matemáticas Capítulo 1
- Clase 12 RD Sharma Solutions Relaciones y funciones Capítulo 1 , Capítulo 2 y Capítulo 3
- Todas las fórmulas importantes para la Clase 12 Capítulo 1
Capítulo 2: Funciones trigonométricas inversas
El Capítulo 2 de Matemáticas de Clase 12 de NCERT, Funciones trigonométricas inversas , cubre una variedad de temas, incluidas notas basadas en conceptos básicos de funciones trigonométricas inversas, propiedades de funciones trigonométricas inversas y ejemplos diversos. Estos principios están bien explicados con ejemplos. En cálculo , las funciones trigonométricas inversas son esenciales porque se utilizan para definir varias integrales . Las funciones trigonométricas inversas tienen aplicaciones en ciencia e ingeniería.
Funciones trigonométricas inversas da cuenta de varios temas, como los gráficos de las funciones trigonométricas inversas , las diferentes propiedades de las funciones trigonométricas inversas , junto con su dominio, rango y otros atributos importantes.
Aquí está la lista de algunas fórmulas importantes cubiertas en CBSE Clase 12 Capítulo 2 – Funciones trigonométricas inversas,
- y = sen −1 x ⇒ x = sen y
- x = sen y ⇒ y = sen −1 x
- sen −1 (1/x) = cosec −1 x
- cos −1 (1/x) = segundo −1 x
- bronceado −1 (1/x) = cuna −1 x
- cos −1 (−x) = π−cos −1 x
- cuna −1 (−x) = π−cot −1 x
- segundo −1 (−x) = π−segundo −1 x
- sen −1 (−x) = −sen −1 x
- tan −1 (−x) = −tan −1 x
- coseg −1 (−x) = −coseg −1 x
- bronceado −1 x + cuna −1 x = π/2
- sen −1 x + cos −1 x = π/2
- coseg −1 x + seg −1 x = π/2
- bronceado −1 x + bronceado −1 y = bronceado −1 {x + y / (1−xy)}
- 2tan −1 x = sin −1 {2x / 1+x 2 } = cos −1 {1−x 2 }/{1+x 2 }
- 2tan −1 x = tan −1 2x / {1−x 2 }
- tan −1 x + tan −1 y = π + tan −1 (x+y / 1−xy); xy > 1; x, y > 0
El capítulo 2 de CBSE Class 12 Maths Notes cubre los siguientes temas:
- Conceptos básicos
- Gráficas de funciones trigonométricas inversas
- Propiedades de las funciones trigonométricas inversas
- Identidades trigonométricas inversas
Más recursos para CBSE Clase 12 Matemáticas Capítulo 2
- Clase 12 Soluciones NCERT Matemáticas Capítulo 2
- Clase 12 RD Sharma Solutions Funciones trigonométricas inversas
- Todas las fórmulas importantes para la Clase 12 Capítulo 2
Capítulo 3: Arrays
Se dice que una Array tiene un arreglo rectangular ordenado de funciones o números. Una array de orden m × n consta de m filas y n columnas. Este capítulo proporciona conocimientos cruciales de arrays que tienen aplicaciones en diferentes áreas, como negocios, ventas, estimación de costos, etc.
Notas de Matemáticas de Clase 12 para el Capítulo 3 Arrays cubre temas tales como tipos de arrays , encontrar cantidades desconocidas usando arrays equivalentes y realizar operaciones aritméticas en arrays . Además, en este capítulo se cubre cómo transponer arrays y luego encontrar la inversa usando diferentes métodos .
Operaciones básicas de arrays que se introducen en CBSE Clase 12 Capítulo 3- Arrays,
- kA = k[aij] metro × norte = [k(aij)] metro × norte
- – A = (– 1)A
- A – B = A + (– 1)B
- A + B = B + A
- (A + B) + C = A + (B + C); donde A, B y C son todos del mismo orden
- k(A + B) = kA + kB; donde A y B son del mismo orden; k es constante
- (k + l)A = kA + lA; donde k y l son la constante
Si A = [a ij ] m × n y B = [b jk ] n × p , entonces
- AB = C = metro × pag ; donde c ik = ∑ norte j=1 a ij segundo jk
- A.(BC) = (AB).C
- A(B + C) = AB + CA
- (A + B)C = AC+ BC
Si A= [a ij ] m × n , entonces A’ o A T = [a ji ] n × m también,
- (A’)’ = A
- (kA)’ = kA’
- (A + B)’ = A’ + B’
- (AB)’ = B’A’
El Capítulo 3 de CBSE Class 12 Math Notes cubre los siguientes temas:
- Arrays y sus tipos
- Operaciones Matemáticas en Arrays
- Propiedades de la suma de arrays y la multiplicación escalar
- Cómo multiplicar arrays
- Transpuesta de una array
- Arrays simétricas y simétricas sesgadas
- Operaciones elementales con arrays
- Inversa de una array por operaciones elementales
- Arrays Invertibles
Más recursos para CBSE Clase 12 Matemáticas Capítulo 3
- Clase 12 Soluciones NCERT Matemáticas Capítulo 3
- Clase 12 RD Sharma Solutions Arrays Capítulo 1 y Capítulo 2
- Todas las fórmulas importantes para la Clase 12 Capítulo 3
Capítulo 4: Determinantes
Las notas de clase para el Capítulo 4 Determinantes demuestran claramente la imagen del determinante de una array cuadrada y la forma de encontrarlo. Las características de los determinantes , menores y cofactores , y las ecuaciones lineales son subtemas importantes que se explican detalladamente en este capítulo.
Este capítulo es una continuación del capítulo anterior de Arrays . Este capítulo ayuda a aprender sobre los determinantes , sus propiedades , cómo se pueden usar los determinantes para calcular el área de un triángulo y para resolver un sistema de ecuaciones lineales .
Aquí está la lista de algunas fórmulas importantes utilizadas para comprender los conceptos en CBSE Clase 12 Capítulo 4- Determinantes,
- Definición de Determinante : Para una array dada, A = [a 11 ] 1 × 1 su determinante se define como det a 11 o |a 11 | = un 11
- Para una array de 2 × 2, X = el determinante se define como,
- Para una array de 3 × 3, A = el determinante se define como |A| =
- El área de un triángulo con vértices (x 1 , y 1 ), (x 2 , y 2 ) y (x 3 , y 3 ) está dada por
- Minor : Si la array dada es:
El Menor de un 12 será el determinante:
- Cofactor : Los cofactores están relacionados con los menores por una pequeña fórmula, para un elemento aij, el cofactor de este elemento es Cij y el menor es M ij entonces, el cofactor se puede escribir como:
C ij = (-1) i+j M ij
- Propiedad escalar múltiple de los determinantes : si cada elemento de una fila (o una columna) de un determinante se multiplica por una constante k, entonces su valor se multiplica por k
- Propiedad de la suma de los determinantes : si algunos o todos los elementos de una fila o columna pueden expresarse como la suma de dos o más términos, entonces el determinante también puede expresarse como la suma de dos o más determinantes.
El capítulo 4 de CBSE Class 12 Maths Notes cubre los siguientes temas:
- Determinantes
- Propiedades de los Determinantes
- Área de un Triángulo usando Determinantes
- Menores y Cofactores
- Adjunto de una array
- Aplicación de Determinantes y Arrays
Más recursos para CBSE Clase 12 Matemáticas Capítulo 4
- Clase 12 Soluciones NCERT Matemáticas Capítulo 4
- Clase 12 RD Sharma Solutions Determinantes Capítulo 1 y Capítulo 2
- Todas las fórmulas importantes para la Clase 12 Capítulo 4
Capítulo 5: Continuidad y Diferenciabilidad
El Capítulo Continuidad y Derivabilidad es la extensión de la Derivación de funciones estudiada en la Clase 11. Ahora, en esta clase, comprenderá funciones, como funciones polinómicas y trigonométricas . Este capítulo se centra en las ideas de continuidad , diferenciabilidad y sus interrelaciones.
Los temas tratados en el Capítulo 5, Continuidad y diferenciabilidad , son cómo diferenciar funciones trigonométricas inversas. Además, aprenderá sobre una nueva clase de funciones conocidas como funciones exponenciales y logarítmicas. Se cubrirán las derivadas de funciones exponenciales y logarítmicas , así como la diferenciación logarítmica . Este capítulo también cubre las ideas de derivadas de funciones en términos de formas paramétricas y derivadas de segundo orden y la introducción a los dos teoremas dados por Rolle y Lagrange .
Principales fórmulas importantes para CBSE Clase 12 Capítulo 5- Continuidad y diferenciabilidad,
- Propiedades relacionadas con la continuidad de una función:
- (f±g)(x) = f(x)±g(x) es continua.
- (fg)(x) = f(x).g(x) es continua.
- fg(x) = f(x)g(x) (siempre que g(x)≠0 sea continua.
- Regla de la string : si f = vou, t = u (x) y si existen tanto dt/dx como dv/dx, entonces:
df/dx = dv/dt. dt/dx
- Teorema de Rolle : Si f: [a, b] → R es continua en [a, b] y derivable en (a, b) donde f(a) = f(b), entonces existe algo de c en (a, b) tal que f ′(c) = 0.
- Teorema del valor medio: Si f : [a, b] → R es continua en [a, b] y derivable en (a, b). Entonces existe alguna c en (a, b) tal que
f′(c) = f(b)−f(a) / b−a
- Fórmulas estándar para derivadas de una función
- d/dx (sen −1 x) = 1/√1−x 2
- d/dx(cos −1 x) = −1/√1−x 2
- d/dx(tan −1 x) = 1/√1+x 2
- d/dx(cot −1 x) = −1/√1+x 2
- d/dx(seg −1 x) = 1/x√1−x 2
- d/dx(coseg −1 x) = −1/x√1−x 2
- d/dx (e x ) = e x
- d/dx (log x) = 1/x
El capítulo 5 de CBSE Class 12 Math Notes cubre los siguientes temas:
- Continuidad y Discontinuidad en Cálculo
- Diferenciabilidad de una función
- Derivadas de funciones inversas
- Derivadas de funciones implícitas
- Derivadas de funciones compuestas
- Derivadas de funciones trigonométricas inversas
- Derivadas de Funciones Exponenciales y Logarítmicas
- Diferenciación logarítmica
- Pruebas para las derivadas de eˣ y ln(x) – Diferenciación avanzada
- Teorema del valor medio de Rolle y Lagrange
- Derivada de funciones en formas paramétricas
- Derivadas de segundo orden en continuidad y diferenciabilidad
- teorema del valor medio
- Álgebra de funciones continuas
Más recursos para CBSE Clase 12 Matemáticas Capítulo 5
- Clase 12 Soluciones NCERT Matemáticas Capítulo 5
- Clase 12 Soluciones RD Sharma Continuidad y diferenciabilidad Capítulo 1 , Capítulo 2 , Capítulo 3 y Capítulo 4
- Todas las fórmulas importantes para la Clase 12 Capítulo 5
Capítulo 6: Aplicaciones de las Derivadas
Aplicaciones de Derivadas en la Clase 12 trata sobre la introducción básica de derivadas , cómo determinar la tasa de cambio de cantidades , encontrar los valores mínimo y máximo de una función y ecuaciones de tangentes y normales a una curva .
Esto no es suficiente para los estudiantes, también hemos cubierto funciones e intervalos crecientes y decrecientes , ecuación de tangentes y normales . Los temas importantes desde el punto de vista del examen se tratan de una manera muy fácil de aprender. Dichos temas son mínimos y máximos relativos y absolutos , puntos críticos , trazado de curvas y aproximaciones .
Fórmulas importantes de Derivados estudiadas en CBSE Clase 12 Capítulo 6- Aplicaciones de Derivados,
(y – f(a))/(x – a) = f'(a)
(y – f(a))/(x – a) = -1/f'(a)
- Prueba de la segunda derivada: cuando la pendiente de una función es cero en x, entonces la segunda derivada f” en ese punto es:
El capítulo 6 de CBSE Class 12 Maths Notes cubre los siguientes temas:
- Puntos críticos
- Derivados como tasa de cambio
- Funciones crecientes y decrecientes
- Intervalos crecientes y decrecientes
- Tangentes y Normales
- Ecuación de Tangentes y Normales
- Mínimos y máximos relativos
- Máximos y mínimos absolutos
- función cóncava
- Puntos de inflexión
- Esbozo de curvas
- Aproximaciones y Máximos y Mínimos – Aplicación de Derivadas
- Derivadas de orden superior
Más recursos para CBSE Clase 12 Matemáticas Capítulo 6
- Clase 12 Soluciones NCERT Matemáticas Capítulo 6
- Clase 12 RD Sharma Solutions Aplicaciones de derivados Capítulo 1 , Capítulo 2 , Capítulo 3 , Capítulo 4 , Capítulo 5 y Capítulo 6
- Todas las fórmulas importantes para la Clase 12 Capítulo 6
Capítulo 7: Integrales
La antiderivada , también conocida como integral , se presenta a los estudiantes en CBSE Notes Class 12 Math Integrals . A los estudiantes se les enseña sobre la representación geométrica de integrales así como también cómo realizar la integración de funciones utilizando numerosos métodos y fórmulas . Además, a los estudiantes se les enseña sobre integrales definidas . En este capítulo, se analizan los métodos para determinar la función cuando se da su derivada y el área bajo la gráfica de una función . Las propiedades básicas de las integrales y el teorema fundamental del cálculo también se incluyen en este capítulo.
La parte más crucial de este capítulo está bien versada en los siguientes enlaces. Dichos temas son varios métodos utilizados para determinar la integración de una función, como la integración por sustitución , la integración mediante fracciones parciales , la integración por partes , la integración mediante identidades trigonométricas , la integración de algunas funciones integrales y la definición y el concepto de integrales definidas . Junto con sumas de Riemann con notación sigma , regla trapezoidal , integral definida como el límite de una suma de Riemann , integrales indefinidas y algunos métodos para determinar integrales definidas comoLa integración por sustitución de U , la regla de la string inversa se analizan en estas notas para las integrales del capítulo 7.
Fórmulas estándar de Integrales estudiadas en CBSE Clase 12 Capítulo 7- Integrales,
- ∫x n dx = x n+ 1/n+1+C, donde n≠−1.
- ∫cos x dx = sen x + C
- ∫sen x dx = −cos x + C
- ∫seg 2x dx = tan x + C
- ∫coseg 2 x dx = −cot x + C
- ∫sec x tan x dx = sec x + C
- ∫cosec x cot x dx = −cosec x + C
- ∫dx / √1−x 2 = sen −1 x + C
- ∫dx / √1−x 2 = -cos −1 x + C
- ∫dx / 1+x 2 = tan −1 x + C
- ∫dx / 1+x 2 = −cot −1 x + C
- ∫e x dx = e x + C
- ∫a x dx = a x log a + C
- ∫dx / x√x 2 −1 = segundo −1 x + C
- ∫dx / x√x 2 −1 = −cosec −1 x + C
- ∫1 / x dx = registro |x| + C
El capítulo 7 de CBSE Class 12 Maths Notes cubre los siguientes temas:
- Introducción a las Integrales
- Integración por Sustitución
- Integración por Fracciones Parciales
- Integración por partes
- Integración mediante identidades trigonométricas
- Funciones definidas por Integrales
- Integrales definidas
- Cálculo de integrales definidas
- Teorema fundamental del cálculo
- Hallar derivadas con el teorema fundamental del cálculo
- Evaluación de Integrales Definidas por Sustitución
- Propiedades de las integrales definidas
- Integrales definidas de funciones por partes
- integrales impropias
- Sumas de Riemann
- Sumas de Riemann con notación sigma
- Regla trapezoidal
- Integral definida como límite de una suma de Riemann
- antiderivadas
- Integrales indefinidas
- Soluciones Particulares a Ecuaciones Diferenciales
- Integración por sustitución de U
- regla de la string inversa
- Expansión en fracciones parciales
- Sustitución trigonométrica
Más recursos para CBSE Clase 12 Matemáticas Capítulo 7
- Clase 12 Soluciones NCERT Matemáticas Capítulo 7
- Clase 12 RD Sharma Solutions Integrals Capítulo 1 y Capítulo 2
- Todas las fórmulas importantes para la Clase 12 Capítulo 7
Capítulo 8: Aplicaciones de las Integrales
A lo largo de este capítulo , Aplicaciones de las integrales , continuaremos discutiendo las integrales . Una aplicación diferente de Integrales como área bajo curvas simples , área de la región delimitada por una curva y una línea, área entre dos curvas y ejemplos misceláneos. Desde los enlaces a continuación, los estudiantes pueden acceder a las notas de los capítulos que explican los conceptos de este capítulo.
Este capítulo también incluyó temas como cómo encontrar el área de diferentes figuras geométricas como círculos , parábolas y elipses .
Fórmulas importantes de Integrales estudiadas en CBSE Clase 12 Capítulo 8- Aplicaciones de Integrales,
- El área encerrada por la curva y = f (x) ; El eje x y las rectas x = a y x = b (b > a) viene dado por la fórmula:
Área = ∫ segundo a y dx=∫ segundo a f (x) dx
- El área de la región delimitada por la curva x = φ (y) como su eje y y las líneas y = c, y = d viene dada por la fórmula:
Área = ∫ re c x dy=∫ re c ϕ(y) dy
- El área encerrada entre las dos curvas dadas y = f (x), y = g (x) y las líneas x = a, x = b viene dada por la siguiente fórmula:
Área = ∫ b a [f(x)−g(x)]dx
donde, f(x) ≥ g(x) en [a,b].
- Si f (x) ≥ g (x) en [a, c] y f (x) ≤ g (x) en , a < c < b, entonces:
Área = ∫ c a [f(x)−g(x)]dx+∫ c a [g(x)−f(x)]dx
El capítulo 8 de CBSE Class 12 Math Notes cubre los siguientes temas:
- Áreas bajo curvas simples
- Área entre dos curvas
- Área definida por Curvas Polares
- Área como integral definida
Más recursos para CBSE Clase 12 Matemáticas Capítulo 8
- Clase 12 Soluciones NCERT Matemáticas Capítulo 8
- Clase 12 RD Sharma Solutions Aplicaciones de integrales
- Todas las fórmulas importantes para la Clase 12 Capítulo 8
Capítulo 9: Ecuaciones diferenciales
En este capítulo, Ecuaciones diferenciales , los estudiantes conocerán el concepto de ecuaciones diferenciales , los conceptos básicos relacionados con las ecuaciones diferenciales, el grado de una ecuación diferencial, el orden de una ecuación diferencial y las soluciones generales y particulares de una ecuación diferencial. La siguiente sección de la unidad cubre la formación de una ecuación diferencial, ecuaciones derivables de primer grado y métodos para resolver ecuaciones de primer orden,
Estos conceptos de ecuaciones diferenciales y cómo encontrar soluciones a una ecuación diferencial son muy útiles en diversas aplicaciones en Física y Economía.
Conceptos importantes discutidos en CBSE Clase 12 Capítulo 9- Ecuaciones diferenciales,
- Orden de la ecuación diferencial: En la ecuación diferencial dada, el mayor orden de la derivada existente en la variable dependiente con respecto a la variable independiente.
- Solución General y Particular de una Ecuación Diferencial : La solución general de la ecuación diferencial es la solución que contiene constantes arbitrarias. Una solución particular de la ecuación diferencial es aquella que está libre de constantes arbitrarias y se produce a partir de la solución general asignando valores particulares a las constantes arbitrarias.
- Métodos para resolver ecuaciones diferenciales de primer orden y primer grado
El capítulo 9 de CBSE Class 12 Math Notes cubre los siguientes temas:
- Conceptos básicos de ecuaciones diferenciales
- Soluciones Particulares a Ecuaciones Diferenciales
- Ecuaciones diferenciales homogéneas
- Ecuaciones diferenciales separables
- Ecuaciones exactas y factores integrantes
- Diferenciación implícita
- Diferenciación implícita: ejemplos avanzados
- Diferenciación Avanzada
- Derivados disfrazados: diferenciación avanzada
- Diferenciación de funciones trigonométricas inversas
- Diferenciación logarítmica
Más recursos para CBSE Clase 12 Matemáticas Capítulo 9
- Clase 12 Soluciones NCERT Matemáticas Capítulo 9
- Clase 12 RD Sharma Solutions Ecuaciones diferenciales
- Todas las fórmulas importantes para la Clase 12 Capítulo 9
Capítulo 10: Álgebra vectorial
En este capítulo, se discuten los conceptos de álgebra vectorial , cómo encontrar el vector de posición de un punto , la interpretación geométrica de vectores y el producto escalar y vectorial de vectores . Estos conceptos tienen gran importancia en la educación superior (ingeniería y tecnología).
Los temas principales tratados en este capítulo incluyen cómo encontrar el vector de posición , algunos conceptos básicos relacionados con el álgebra vectorial , los cosenos directores , los tipos de vectores como el vector cero, el vector unitario, el vector colineal, el vector igual, el negativo de un vector, la suma de vectores, propiedades de la suma de vectores . Junto con la multiplicación de un vector por un escalar, componentes de un vector, vector que une dos puntos, fórmula de sección, producto de dos vectores , producto escalar o escalar de dos vectores , propiedades del producto escalar, proyección de un vector en una línea , vector o producto cruzadode dos vectores se discuten en este capítulo.
Aquí hay fórmulas muy importantes para CBSE Clase 12 Capítulo 10- Álgebra vectorial,
- Ley Conmutativa – A + B = B + A
- Ley Asociativa – A + (B + C) = (A + B) + C
- Producto escalar – (A • B )= |P| |P| cos θ
- Producto Cruzado – (A × B )= |P| |P| sen θ
- k (A + B )= kA + kB
- Identidad Aditiva – A + 0 = 0 + A
El capítulo 10 de CBSE Class 12 Maths Notes cubre los siguientes temas:
- Introducción al Álgebra Vectorial
- Producto de dos vectores
- ¿Cómo encontrar el ángulo entre dos vectores?
- Fórmula de sección
Más recursos para CBSE Clase 12 Matemáticas Capítulo 10
- Clase 12 Soluciones NCERT Matemáticas Capítulo 10
- Clase 12 RD Sharma Solutions Álgebra vectorial Capítulo 1 , Capítulo 2 , Capítulo 3 y Capítulo 4
- Todas las fórmulas importantes para la Clase 12 Capítulo 10
Capítulo 11: Geometría tridimensional
Basado en el álgebra vectorial discutida en el capítulo anterior, aquí están los conceptos como, cómo se puede aplicar a la geometría tridimensional. Además, en esta parte se analiza la introducción a temas como los cosenos de dirección y las razones de dirección, las ecuaciones cartesianas y vectoriales de una línea, y cómo encontrar la distancia más corta entre dos líneas utilizando estos conceptos.
Aquí están las fórmulas más importantes para CBSE Clase 12 Capítulo 11- Geometría tridimensional,
- Ecuación cartesiana de un plano: lx + my + nz = d
- Distancia entre dos puntos P(x 1 , y 1 , z 1 ) y Q(x 2 , y 2 , z 2 ): PQ = √ ((x 1 – x 2 ) 2 + (y 1 – y 2 )2 + (z 1 – z 2 ) 2 )
El capítulo 11 de CBSE Class 12 Maths Notes cubre los siguientes temas:
- Cosenos de dirección y razones de dirección de una línea
- Ecuación de una Línea en 3D
- Ángulo entre dos rectas
- Distancia más corta entre dos líneas en el espacio 3D
- Puntos, Líneas y Planos
Más recursos para CBSE Clase 12 Matemáticas Capítulo 11
- Clase 12 Soluciones NCERT Matemáticas Capítulo 11
- Clase 12 RD Sharma Solutions Geometría tridimensional Capítulo 1 , Capítulo 2 y Capítulo 3
- Todas las fórmulas importantes para la Clase 12 Capítulo 11
Capítulo 12: Programación lineal
Este capítulo es una continuación de los conceptos de desigualdades lineales y el sistema de ecuaciones lineales en dos variables estudiados en la clase anterior. Este capítulo ayuda a aprender cómo se pueden aplicar estos conceptos para resolver problemas del mundo real y cómo optimizar los problemas de programación lineal para que uno pueda maximizar la utilización de recursos, minimizar las ganancias, etc.
Conceptos importantes estudiados en CBSE Clase 12 Capítulo 12- Programación lineal,
- La región común determinada por todas las restricciones, incluidas las restricciones no negativas x ≥ 0, y ≥ 0 de un problema de programación lineal, se denomina región factible (o región de solución) del problema.
- Los puntos dentro y sobre el límite de la región factible representan soluciones factibles de las restricciones. Cualquier punto fuera de la región factible es una solución no factible .
- Cualquier punto en la región factible que da el valor óptimo (máximo o mínimo) de la función objetivo se llama solución óptima .
El capítulo 12 de CBSE Class 12 Maths Notes cubre los siguientes temas:
Más recursos para CBSE Clase 12 Matemáticas Capítulo 12
- Clase 12 Soluciones NCERT Matemáticas Capítulo 12
- Clase 12 RD Sharma Solutions Programación lineal
- Todas las fórmulas importantes para la Clase 12 Capítulo 12
Capítulo 13: Probabilidad
Este capítulo trata sobre la probabilidad , el concepto de probabilidad también se estudió en clases anteriores. Este capítulo de la presente clase ayuda a aprender acerca de la probabilidad condicional . Además, en este capítulo se tratan temas como el teorema de Bayes , la independencia de eventos , la distribución de probabilidad de variables aleatorias , la media y la varianza de una distribución de probabilidad y la distribución binomial .
Fórmulas importantes estudiadas en CBSE Clase 12 Capítulo 13- Probabilidad,
- La probabilidad condicional de un evento E mantiene el valor de la ocurrencia del evento F como:
P(E|F) = E ∩ F / P(F), P(F)≠0
- Probabilidad Total : Sea E 1 , E 2 , …. , E n la partición de un espacio muestral y A cualquier evento; después,
PAGS(A) = PAGS(E 1 ) PAGS (A|E 1 ) + PAGS (E 2 ) PAGS (A|E 2 ) + … + PAGS (E n ) . P(A|E n )
- Teorema de Bayes : Si E 1 , E 2 , …. , E n son eventos que constituyen un espacio muestral S; después,
P(E yo |A) = P(E yo ) P(A|E yo ) / ∑ norte j=1 P(Ej) P(A|Ej)
- Var (X) = E (X 2 ) – [E (X)] 2
El capítulo 13 de CBSE Class 12 Maths Notes cubre los siguientes temas:
- Probabilidad Condicional e Independencia
- Teorema de la multiplicación
- Eventos dependientes e independientes
- Teorema de Bayes
- Distribución de probabilidad
- Variables aleatorias binomiales y distribución binomial
- Media binomial y desviación estándar
- Pruebas de Bernoulli y distribución binomial
- Variables aleatorias discretas
- Valor esperado
Más recursos para CBSE Clase 12 Matemáticas Capítulo 13
- Clase 12 Soluciones NCERT Matemáticas Capítulo 13
- Probabilidad de soluciones RD Sharma Clase 12
- Todas las fórmulas importantes para la Clase 12 Capítulo 1
Recursos importantes para CBSE Class 12th proporcionados por GeeksforGeeks: –
- NCERT Soluciones Matemáticas Clase 12
- RD Sharma Soluciones Matemáticas Clase 12
- CBSE Clase 12 Fórmulas Matemáticas
- Notas de clase 12 de física CBSE
- Notas de química CBSE Clase 11
- CBSE Clase 12 Matemáticas Término 1 2021 Clave de respuestas
Preguntas frecuentes (FAQ)
Pregunta 1: ¿Cuáles son los temas principales que se cubren en Clase 12 Matemáticas Capítulo 5 Continuidad y diferenciabilidad?
Responder:
Los temas principales que se tratan en el Capítulo 5, Continuidad y diferenciabilidad, son la continuidad de una función y la realización de operaciones algebraicas en funciones continuas. Otros temas incluidos que son esenciales para los exámenes son encontrar las derivadas de funciones compuestas, implícitas, trigonométricas, exponenciales y logarítmicas, la diferenciación de funciones en forma paramétrica, derivadas de segundo orden, el teorema del valor medio y la regla de la string para la diferenciación.
Pregunta 2: ¿Cuáles son algunos consejos importantes para estudiar el Capítulo 9 Ecuaciones diferenciales en la Clase 9?
Responder:
Las Notas de Matemáticas de la Clase 12 de CBSE para el Capítulo 9 pueden guiar a los estudiantes a superar las dificultades y tratar de comprender los conceptos de cálculo. Los estudiantes pueden usar los consejos de estudio que se enumeran a continuación para ayudarlos a acelerar su aprendizaje.
- Antes de sumergirse en las ecuaciones diferenciales, asegúrese de haber completado los capítulos anteriores.
- Haz una lista de fórmulas y toma notas.
- Practique regularmente.
Pregunta 3: ¿De qué manera estas Notas de Matemáticas CBSE Clase 12 son útiles para los estudiantes en sus exámenes de la junta?
Responder:
Al intentar los exámenes de la junta, los estudiantes deben preparar sus trabajos en un formato que las personas que los corregirán puedan entender fácilmente. Las soluciones NCERT incluyen una explicación detallada y paso a paso que enseña a los estudiantes cómo resolver cualquier problema. Debido a que a cada paso se le asigna un conjunto de calificaciones, los estudiantes que siguen el patrón de estas soluciones NCERT seguramente recibirán la calificación más alta posible.
Publicación traducida automáticamente
Artículo escrito por mayurigrover y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA