Ver notas de última hora sobre todos los temas aquí .
Lógica proposicional
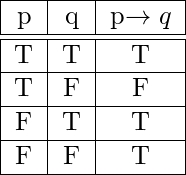
- Implicación( →) : Para dos proposiciones cualesquiera p y q, el enunciado “si p entonces q” se llama implicación y se denota por p → q.
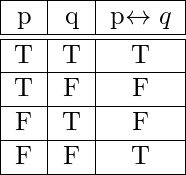
- si y solo si(↔) : Para dos proposiciones cualesquiera p y q, el enunciado “p si y solo si(si) q” se llama bicondicional y se denota por p ↔ q.
Ley de De Morgan :
Declaraciones condicionales especiales
1. Implicación: ![]()
2. Inversa : La inversa de la proposición ![]() es
es ![]()
3. Contrapositiva: La contrapositiva de la proposición ![]() es
es ![]()
4. Inversa: La inversa de la proposición ![]() es
es![]()
Tipos de proposiciones basadas en valores de verdad
1. Tautología : una proposición que siempre es verdadera se denomina tautología.
2. Contradicción : una proposición que siempre es falsa se llama contradicción.
3. Contingencia : una proposición que no es ni una tautología ni una contradicción se llama contingencia.
Hay dos equivalencias muy importantes que involucran cuantificadores
1.2.
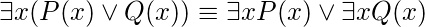
Reglas de inferencia![Rendered by QuickLaTeX.com \begin{tabular}{||c||c||c||} \hline Rule of Inference & Tautology & Name\\ \hline \rule{0pt}{8ex} \shortstack[l]{p \\ p\rightarrow q \\ \rule{1cm}{0.5pt}\\ \therefore q}& (p\wedge (p\rightarrow q)) \rightarrow q & Modus Ponens \\ \hline \rule{0pt}{8ex} \shortstack[l]{\neg q \\ p\rightarrow q \\ \rule{1cm}{0.5pt}\\ \therefore \neg p}& (\neg q \wedge (p\rightarrow q)) \rightarrow \neg p & Modus Tollens \\ \hline \rule{0pt}{8ex} \shortstack[l]{p\rightarrow q \\ q\rightarrow r \\ \rule{1.3cm}{0.5pt}\\ \therefore p \rightarrow r}& ((p\rightarrow q) \wedge (q\rightarrow r)) \rightarrow (p\rightarrow r) & Hypothetical syllogism \\ \hline \rule{0pt}{8ex} \shortstack[l]{ \neg p \\ p\vee q \\ \rule{0.8cm}{0.5pt}\\ \therefore q} & (\neg p \wedge (p\vee q)) \rightarrow q & Disjunctive Syllogism \\ \hline \rule{0pt}{8ex} \shortstack[l]{p \\ \rule{1.5cm}{0.5pt} \\ \therefore (p \vee q)}& p\rightarrow (p\vee q) & Addition \\ \hline \rule{0pt}{8ex} \shortstack[l]{ (p\wedge q)\rightarrow r \\ \rule{2.3cm}{0.5pt}\\ \therefore p\rightarrow (q\rightarrow r)} & ((p\wedge q)\rightarrow r) \rightarrow (p\rightarrow (q\rightarrow r)) & Exportation\\ \hline \rule{0pt}{8ex} \shortstack[l]{p\vee q\\\neg p\vee r \\ \rule{1.2cm}{0.5pt} \\ \therefore q\vee r}& ((p\vee q) \wedge(\neg p\vee r)) \rightarrow q\vee r & Resolution \\ \hline \end{tabular}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-29c02691ae71fa01c415b7cfe073d1b5_l3.png)
Combinatría
Permutación : una permutación de un conjunto de objetos distintos es un arreglo ordenado de estos objetos.
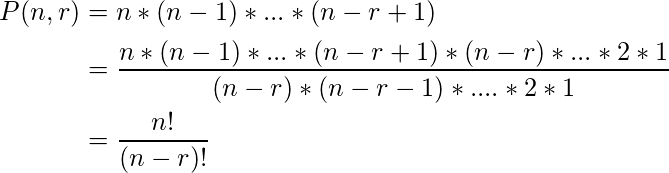
Combinación : una combinación de un conjunto de objetos distintos es solo un recuento de la cantidad de formas en que se puede seleccionar una cantidad específica de elementos de un conjunto de cierto tamaño. El orden de los elementos no importa en una combinación. ![]()
que nos da-
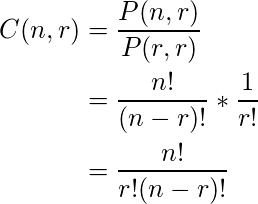
Coeficientes binomiales : Las ![]() combinaciones de un conjunto de
combinaciones de un conjunto de ![]() elementos si se denotan por
elementos si se denotan por ![]() . Este número también se llama coeficiente binomial ya que aparece como un coeficiente en la expansión de potencias de expresiones binomiales.
. Este número también se llama coeficiente binomial ya que aparece como un coeficiente en la expansión de potencias de expresiones binomiales.
Sean ![]() y
y ![]() sean variables y
sean variables y ![]() sean un entero no negativo. Después
sean un entero no negativo. Después
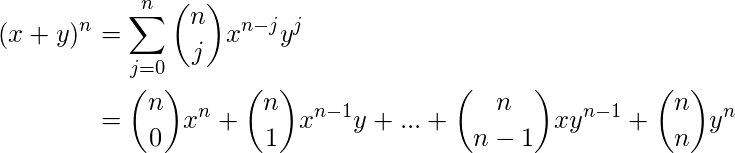
La expansión binomial usando símbolos combinatorios
Teoría de conjuntos
Un conjunto es una colección desordenada de objetos, conocidos como elementos o miembros del conjunto.
Un elemento ‘a’ perteneciente a un conjunto A puede escribirse como ‘a ∈ A’, ‘a ∉ A’ denota que a no es un elemento del conjunto A.
Conjuntos iguales
Se dice que dos conjuntos son iguales si ambos tienen los mismos elementos. Por ejemplo A = {1, 3, 9, 7} y B = {3, 1, 7, 9} son conjuntos iguales.
NOTA: El orden de los elementos de un conjunto no importa.
Subconjunto
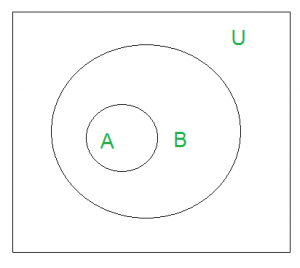
Se dice que un conjunto A es subconjunto de otro conjunto B si y solo si cada elemento del conjunto A es también parte de otro conjunto B.
Denotado por ‘ ⊆ ‘.
‘A ⊆ B ‘ denota que A es un subconjunto de B.
Para demostrar que A es el subconjunto de B, simplemente debemos demostrar que si x pertenece a A, entonces x también pertenece a B.
Para demostrar que A no es un subconjunto de B, debemos encontrar un elemento que sea parte del conjunto A. pero no pertenecen al conjunto B.
‘U’ denota el conjunto universal. El diagrama de Venn anterior muestra que A es un subconjunto de B.
Tamaño de un conjunto El
tamaño de un conjunto puede ser finito o infinito.
Por ejemplo
Finite set: Set of natural numbers less than 100. Infinite set: Set of real numbers.
El tamaño del conjunto S se conoce como número de Cardinalidad , denotado como |S|.
Nota: La cardinalidad de un conjunto nulo es 0.
Conjuntos
potencia El conjunto potencia es el conjunto de todos los subconjuntos posibles del conjunto S. Denotado por P(S).
Ejemplo: ¿Cuál es el conjunto potencia de {0, 1, 2}?
Solución: Todos los subconjuntos posibles
{∅}, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}.
Nota: el conjunto vacío y el propio conjunto también son miembros de este conjunto de subconjuntos.
La cardinalidad del conjunto potencia es ![]() , donde n es el número de elementos en un conjunto.
, donde n es el número de elementos en un conjunto.
Productos cartesianos
Sean A y B dos conjuntos. El producto cartesiano de A y B se denota por A × B, es el conjunto de todos los pares ordenados (a, b), donde a pertenece a A y b pertenece a B.
A × B = {(a, b) | a ∈ A ∧ b ∈ B}.
La cardinalidad de A × B es N*M, donde N es la cardinalidad de A y M es la cardinalidad de B.
Nota: A × B no es lo mismo que B × A.
Unión
Unión de los conjuntos A y B, denotada por A ∪ B, es el conjunto de elementos distintos que pertenece al conjunto A o al conjunto B, oa ambos.
Intersección
La intersección de los conjuntos A y B, denotada por A ∩ B, es el conjunto de elementos que pertenecen tanto a A como a B, es decir, conjunto del elemento común en A y B.
Disjuntos
Se dice que dos conjuntos son disjuntos si su intersección es el conjunto vacío, es decir, los conjuntos no tienen elementos comunes.
Diferencia de conjunto La
diferencia entre conjuntos se denota por ‘A – B’, es el conjunto que contiene elementos del conjunto A pero no en B. Es decir, todos los elementos de A excepto el elemento de B.
Complemento
El complemento de un conjunto A, denotado por ![]() , es el conjunto de todos los elementos excepto A. El complemento del conjunto A es U – A.
, es el conjunto de todos los elementos excepto A. El complemento del conjunto A es U – A.
- Fórmula:
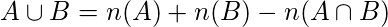
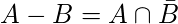
Grupo
Un conjunto no vacío G, (G, *) se llama grupo si sigue el siguiente axioma:
- Cierre: (a*b) pertenece a G para todo a, b ∈ GRAMO.
- Asociatividad: a*(b*c) = (a*b)*c ∀ a, b, c pertenece a G.
- Elemento de Identidad: Existe e ∈ G tal que a*e = e*a = a ∀ a ∈ GRAMO
- Inversos: ∀ a ∈ G existe un -1 ∈ G tal que a*a -1 = a -1 *a = e
relaciones y funciones
|A| = my |B| = n, luego
1. No. de funciones de A a B = n m
2. No. de funciones biunívocas = (n, P, m)
3. No. de funciones sobre =n m – (n, C, 1)*(n-1) m + (n, C, 2)*(n-2) m …. +(-1) m *(n, C, n-1), si m >= n; 0 en caso contrario
4. Condición necesaria para la función biyectiva |A| = |B|
5. El nro. de función biyectiva =n!
6. No. de relaciones =2 mn
7. No. de relaciones reflexivas =2 n(n-1)
8. No. de relaciones simétricas = 2 n(n+1)/2
9. No. de relaciones antisimétricas = 2 n *3 n(n-1)/2
10. Nº de relaciones asimétricas = 3 n(n-1)/2
11. Nº de relaciones irreflexivas = 2 n(n-1)
12. Una relación es un orden parcial si
1) Reflexive
2) Antisymmetric
3) Transitive
13. Conozca a Semi Lattice:
For all a, b belongs to L a∧b exists
14. Únete a Semi Celosía
For all a, b belongs to L a∨b exists
15. Un poset se llama Celosía si se encuentra y se une a la semi-retícula
16. Celosía Complementada: Cada elemento tiene complemento
17. Celosía Distributiva: Cada Elemento tiene cero o 1 complemento.
18. Celosía Booleana: Debe ser a la vez complementada y distributiva. Cada elemento tiene exactamente un complemento.
19. Una relación es una equivalencia si
1) Reflexive
2) symmetric
3) Transitive
Teoría de grafos
1. Número de aristas en un gráfico completo = n(n-1)/2
2. Gráfico bipartito: no hay aristas entre dos vértices cualesquiera de la misma partición. En el gráfico bipartito completo no. de aristas =m*n
3. La suma de los grados de todos los vértices es igual al doble del número de aristas.
4. Número máximo de componentes conexas en gráfico con n vértices = n
5. Número mínimo de componentes conexas =
0 (null graph) 1 (not null graph)
6. Número mínimo de aristas para tener grafo conexo con n vértices = n-1
7. Para garantizar que un grafo con n vértices es conexo, mínimo no. de aristas requeridas = {(n-1)*(n-2)/2 } + 1
8. Un grafo es grafo de euler si existen como máximo 2 vértices de grado impar
9. Árbol
-> Has exactly one path btw any two vertices
-> not contain cycle
-> connected
-> no. of edges = n -1
10. Para el gráfico completo, el no. de árbol de expansión posible = n n-2
- 11. Para gráfico plano conexo simple
- Un grafo es plano si y solo si no contiene una subdivisión de K 5 y K 3, 3 como subgrafo.
- Sea G un grafo plano conexo y n, m y f denoten, respectivamente, el número de vértices, aristas y caras en un dibujo plano de G. Entonces n – m + f = 2.
- Sea G un grafo simple plano conexo con n vértices y m aristas, y sin triángulos. Entonces m ≤ 2n – 4.
- Sea G un grafo plano simple conexo con n vértices, donde n ? 3 y m bordes. Entonces m ≤ 3n – 6.
- 12.) Cada gráfico bipartito es 2 coloreable y viceversa
13.) El no. de coincidencias perfectas para un gráfico completo (2n)/(2 n n!)
14.) El no. de coincidencias completas para K n.n = n!
Publicación traducida automáticamente
Artículo escrito por VaibhavRai3 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA