Dada una string str y consultas Q. Cada consulta consta de un entero K . La tarea es encontrar el número de formas de elegir K substrings iguales de cualquier longitud posible para cada consulta. Tenga en cuenta que el conjunto de K substrings debe ser único.
Ejemplos:
Entrada: str = “aabaab”, que[] = {3}
Salida: 4
“a” es la única substring que aparece más de 3 veces, es decir, 4.
Y hay 4 formas de elegir 3 strings diferentes de las 4 dadas instrumentos de cuerda.
Entrada: str = “aggghh”, que[] = {1, 2, 3}
Salida:
21
5
1
Planteamiento: Se pueden seguir los siguientes pasos para resolver el problema y responder todas las consultas en el mínimo tiempo posible.
- Genere todas las substrings para una string y cuente la aparición de cada substring única mediante hashing.
- Para cada consulta, la respuesta será elegir K substrings de cada string que ocurra más de K veces (digamos X). la respuesta sera
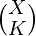
- La complejidad del tiempo por consulta se puede reducir calculando previamente el coeficiente binomial
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
#define maxlen 100
// Function to generate all the sub-strings
void generateSubStrings(string s, unordered_map<string,
int>& mpp)
{
// Length of the string
int l = s.length();
// Generate all sub-strings
for (int i = 0; i < l; i++) {
string temp = "";
for (int j = i; j < l; j++) {
temp += s[j];
// Count the occurrence of
// every sub-string
mpp[temp] += 1;
}
}
}
// Compute the Binomial Coefficient
void binomialCoeff(int C[maxlen][maxlen])
{
int i, j;
// Calculate value of Binomial Coefficient
// in bottom up manner
for (i = 0; i < 100; i++) {
for (j = 0; j < 100; j++) {
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
// Function to return the result for a query
int answerQuery(unordered_map<string, int>& mpp,
int C[maxlen][maxlen], int k)
{
int ans = 0;
// Iterate for every
// unique sub-string
for (auto it : mpp) {
// Count the combinations
if (it.second >= k)
ans += C[it.second][k];
}
return ans;
}
// Driver code
int main()
{
string s = "aabaab";
// Get all the sub-strings
// Store the occurrence of
// all the sub-strings
unordered_map<string, int> mpp;
generateSubStrings(s, mpp);
// Pre-computation
int C[maxlen][maxlen];
memset(C, 0, sizeof C);
binomialCoeff(C);
// Queries
int queries[] = { 2, 3, 4 };
int q = sizeof(queries) / sizeof(queries[0]);
// Perform queries
for (int i = 0; i < q; i++)
cout << answerQuery(mpp, C, queries[i]) << endl;
return 0;
}
Java
// Java implementation of the approach
import java.util.HashMap;
class GFG
{
static int maxlen = 100;
// Function to generate all the sub-strings
public static void generateSubStrings(
String s, HashMap<String,
Integer> mpp)
{
// Length of the string
int l = s.length();
// Generate all sub-strings
for (int i = 0; i < l; i++)
{
String temp = "";
for (int j = i; j < l; j++)
{
temp += s.charAt(j);
// Count the occurrence of
// every sub-string
if (mpp.containsKey(temp))
{
int x = mpp.get(temp);
mpp.put(temp, ++x);
}
else
mpp.put(temp, 1);
}
}
}
// Compute the Binomial Coefficient
public static void binomialCoeff(int[][] C)
{
int i, j;
// Calculate value of Binomial Coefficient
// in bottom up manner
for (i = 1; i < 100; i++)
{
for (j = 0; j < 100; j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
}
// Function to return the result for a query
public static int answerQuery(HashMap<String,
Integer> mpp,
int[][] C, int k)
{
int ans = 0;
// Iterate for every
// unique sub-string
for (HashMap.Entry<String,
Integer> entry : mpp.entrySet())
{
// Count the combinations
if (entry.getValue() >= k)
ans += C[entry.getValue()][k];
}
return ans;
}
// Driver code
public static void main(String[] args)
{
String s = "aabaab";
// Get all the sub-strings
// Store the occurrence of
// all the sub-strings
HashMap<String,
Integer> mpp = new HashMap<>();
generateSubStrings(s, mpp);
// Pre-computation
int[][] C = new int[maxlen][maxlen];
binomialCoeff(C);
// Queries
int[] queries = { 2, 3, 4 };
int q = queries.length;
// Perform queries
for (int i = 0; i < q; i++)
System.out.println(answerQuery(mpp, C,
queries[i]));
}
}
// This code is contributed by
// sanjeev2552
Python3
# Python3 implementation of the approach from collections import defaultdict maxlen = 100 # Function to generate all the sub-strings def generateSubStrings(s, mpp): # Length of the string l = len(s) # Generate all sub-strings for i in range(0, l): temp = "" for j in range(i, l): temp += s[j] # Count the occurrence of # every sub-string mpp[temp] += 1 # Compute the Binomial Coefficient def binomialCoeff(C): # Calculate value of Binomial # Coefficient in bottom up manner for i in range(0, 100): for j in range(0, 100): # Base Cases if j == 0 or j == i: C[i][j] = 1 # Calculate value using previously # stored values else: C[i][j] = C[i - 1][j - 1] + C[i - 1][j] # Function to return the result for a query def answerQuery(mpp, C, k): ans = 0 # Iterate for every # unique sub-string for it in mpp: # Count the combinations if mpp[it] >= k: ans += C[mpp[it]][k] return ans # Driver code if __name__ == "__main__": s = "aabaab" # Get all the sub-strings # Store the occurrence of # all the sub-strings mpp = defaultdict(lambda:0) generateSubStrings(s, mpp) # Pre-computation C = [[0 for i in range(maxlen)] for j in range(maxlen)] binomialCoeff(C) # Queries queries = [2, 3, 4] q = len(queries) # Perform queries for i in range(0, q): print(answerQuery(mpp, C, queries[i])) # This code is contributed by Rituraj Jain
C#
// C# code to print level order
// traversal in sorted order
using System;
using System.Collections.Generic;
class GFG
{
static int maxlen = 100;
// Function to generate all the sub-strings
public static void generateSubStrings(String s,
Dictionary<String, int> mpp)
{
// Length of the string
int l = s.Length;
// Generate all sub-strings
for (int i = 0; i < l; i++)
{
String temp = "";
for (int j = i; j < l; j++)
{
temp += s[j];
// Count the occurrence of
// every sub-string
if (mpp.ContainsKey(temp))
{
mpp[temp] = ++mpp[temp];
}
else
mpp.Add(temp, 1);
}
}
}
// Compute the Binomial Coefficient
public static void binomialCoeff(int[,] C)
{
int i, j;
// Calculate value of Binomial Coefficient
// in bottom up manner
for (i = 1; i < 100; i++)
{
for (j = 0; j < 100; j++)
{
// Base Cases
if (j == 0 || j == i)
C[i, j] = 1;
// Calculate value using previously
// stored values
else
C[i, j] = C[i - 1, j - 1] +
C[i - 1, j];
}
}
}
// Function to return the result for a query
public static int answerQuery(Dictionary<String, int> mpp,
int[,] C, int k)
{
int ans = 0;
// Iterate for every
// unique sub-string
foreach(KeyValuePair<String, int> entry in mpp)
{
// Count the combinations
if (entry.Value >= k)
ans += C[entry.Value, k];
}
return ans;
}
// Driver code
public static void Main(String[] args)
{
String s = "aabaab";
// Get all the sub-strings
// Store the occurrence of
// all the sub-strings
Dictionary<String,
int> mpp = new Dictionary<String,
int>();
generateSubStrings(s, mpp);
// Pre-computation
int[,] C = new int[maxlen, maxlen];
binomialCoeff(C);
// Queries
int[] queries = { 2, 3, 4 };
int q = queries.Length;
// Perform queries
for (int i = 0; i < q; i++)
Console.WriteLine(answerQuery(mpp, C,
queries[i]));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// JavaScript implementation of the approach
let maxlen = 100;
// Function to generate all the sub-strings
function generateSubStrings(s,mpp)
{
// Length of the string
let l = s.length;
// Generate all sub-strings
for (let i = 0; i < l; i++)
{
let temp = "";
for (let j = i; j < l; j++)
{
temp += s[j];
// Count the occurrence of
// every sub-string
if (mpp.has(temp))
{
let x = mpp.get(temp);
mpp.set(temp, ++x);
}
else
mpp.set(temp, 1);
}
}
}
// Compute the Binomial Coefficient
function binomialCoeff(C)
{
let i, j;
// Calculate value of Binomial Coefficient
// in bottom up manner
for (i = 1; i < 100; i++)
{
for (j = 0; j < 100; j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
}
// Function to return the result for a query
function answerQuery(mpp,C,k)
{
let ans = 0;
// Iterate for every
// unique sub-string
for (let[key,value] of mpp.entries())
{
// Count the combinations
if (value >= k)
ans += C[value][k];
}
return ans;
}
// Driver code
let s = "aabaab";
// Get all the sub-strings
// Store the occurrence of
// all the sub-strings
let mpp = new Map();
generateSubStrings(s, mpp);
// Pre-computation
let C = new Array(maxlen);
for(let i=0;i<maxlen;i++)
{
C[i]=new Array(maxlen);
for(let j=0;j<maxlen;j++)
C[i][j]=0;
}
binomialCoeff(C);
// Queries
let queries = [ 2, 3, 4 ];
let q = queries.length;
// Perform queries
for (let i = 0; i < q; i++)
document.write(answerQuery(mpp, C,
queries[i])+"<br>");
// This code is contributed by rag2127
</script>
10 4 1
Complejidad de tiempo: O (max (100 * 100, N * N)), ya que estamos usando bucles anidados para atravesar N * N y 100 * 100 veces. Donde N es la longitud de la string.
Espacio auxiliar: O(max(100*100,N*N)), ya que estamos usando espacio adicional para el mapa y la array C. Donde N es la longitud de la string.