En combinatoria, los números de Narayana N(n, k) , n = 1, 2, 3…, 1 ≤ k ≤ n, forman una array triangular de números naturales, llamada triángulo de Narayana. Está dado por: 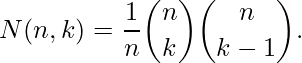
Los números de Narayana N(n, k) se pueden usar para encontrar el número de expresiones que contienen n pares de paréntesis, que coinciden correctamente y que contienen k anidamientos distintos.
Por ejemplo, N(4, 2) = 6 como con cuatro pares de paréntesis, se pueden crear seis secuencias, cada una de las cuales contiene dos veces el subpatrón ‘()’:
()((())) (())(()) (()(())) ((()())) ((())()) ((()))()
Ejemplos:
Input : n = 6, k = 2 Output : 15 Input : n = 8, k = 5 Output : 490
A continuación se muestra la implementación de encontrar N(n, k) :
C++
// CPP program to find Narayana number N(n, k)
#include<bits/stdc++.h>
using namespace std;
// Return product of coefficient terms in formula
int productofCoefficient(int n, int k)
{
int C[n + 1][k + 1];
// Calculate value of Binomial Coefficient
// in bottom up manner
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
return C[n][k] * C[n][k - 1];
}
// Returns Narayana number N(n, k)
int findNN(int n, int k)
{
return (productofCoefficient(n, k)) / n;
}
// Driven Program
int main()
{
int n = 8, k = 5;
cout << findNN(n, k) << endl;
return 0;
}
Java
// Java program to find
// Narayana number N(n, k)
class GFG
{
// Return product of coefficient
// terms in formula
static int productofCoefficient(int n,
int k)
{
int C[][] = new int[n + 1][k + 1];
// Calculate value of Binomial
// Coefficient in bottom up manner
for (int i = 0; i <= n; i++)
{
for (int j = 0;
j <= Math.min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using
// previously stored values
else
C[i][j] = C[i - 1][j - 1]
+ C[i - 1][j];
}
}
return C[n][k] * C[n][k - 1];
}
// Returns Narayana number N(n, k)
static int findNN(int n, int k)
{
return (productofCoefficient(n, k)) / n;
}
// Driver code
public static void main (String[] args)
{
int n = 8, k = 5;
System.out.println(findNN(n, k));
}
}
// This code is contributed by Anant Agarwal.
Python3
# Python3 program to find Narayana number N(n, k) # Return product of coefficient terms in formula def productofCoefficient(n, k): C = [[0 for x in range(k+1)] for y in range(n+1)] # Calculate value of Binomial Coefficient # in bottom up manner for i in range(0, n+1): for j in range(0, min(i+1,k+1)): # Base Cases if (j == 0 or j == i): C[i][j] = 1 # Calculate value using previously # stored values else : C[i][j] = C[i - 1][j - 1] + C[i - 1][j] return C[n][k] * C[n][k - 1] # Returns Narayana number N(n, k) def findNN(n, k): return (productofCoefficient(n, k)) / n # Driven Program n = 8 k = 5 print(int(findNN(n, k))) # This code is contributed by Prasad Kshirsagar
C#
// C# program to find
// Narayana number N(n, k)
using System;
class GFG {
// Return product of coefficient
// terms in formula
static int productofCoefficient(int n,
int k)
{
int[, ] C = new int[n + 1, k + 1];
// Calculate value of Binomial
// Coefficient in bottom up manner
for (int i = 0; i <= n; i++) {
for (int j = 0;
j <= Math.Min(i, k); j++) {
// Base Cases
if (j == 0 || j == i)
C[i, j] = 1;
// Calculate value using
// previously stored values
else
C[i, j] = C[i - 1, j - 1]
+ C[i - 1, j];
}
}
return C[n, k] * C[n, k - 1];
}
// Returns Narayana number N(n, k)
static int findNN(int n, int k)
{
return (productofCoefficient(n, k)) / n;
}
// Driver code
public static void Main()
{
int n = 8, k = 5;
Console.WriteLine(findNN(n, k));
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP program to find
// Narayana number N(n, k)
// Return product of
// coefficient terms
// in formula
function productofCoefficient($n, $k)
{
$C = array(array());
// Calculate value of
// Binomial Coefficient
// in bottom up manner
for ($i = 0; $i <= $n; $i++)
{
for ($j = 0; $j <= min($i, $k); $j++)
{
// Base Cases
if ($j == 0 || $j == $i)
$C[$i][$j] = 1;
// Calculate value
// using previously
// stored values
else
$C[$i][$j] = $C[$i - 1][$j - 1] +
$C[$i - 1][$j];
}
}
return $C[$n][$k] * $C[$n][$k - 1];
}
// Returns Narayana
// number N(n, k)
function findNN( $n, $k)
{
return (productofCoefficient($n, $k)) /$n;
}
// Driver Program
$n = 8;
$k = 5;
echo findNN($n, $k) ;
// This code is contributed by anuj_67.
?>
Javascript
<script>
// javascript program to find
// Narayana number N(n, k)
// Return product of coefficient
// terms in formula
function productofCoefficient(n, k)
{
let C = new Array(n + 1);
// Loop to create 2D array using 1D array
for (var i = 0; i < C.length; i++) {
C[i] = new Array(2);
}
// Calculate value of Binomial
// Coefficient in bottom up manner
for (let i = 0; i <= n; i++)
{
for (let j = 0;
j <= Math.min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using
// previously stored values
else
C[i][j] = C[i - 1][j - 1]
+ C[i - 1][j];
}
}
return C[n][k] * C[n][k - 1];
}
// Returns Narayana number N(n, k)
function findNN(n, k)
{
return (productofCoefficient(n, k)) / n;
}
// Driver code
let n = 8, k = 5;
document.write(findNN(n, k));
</script>
Producción:
490
Complejidad temporal: O(n*n)
complejidad espacial: O((n+1)*(k+1))