Dado un grafo conexo no dirigido y dos vértices A y B , la tarea es encontrar el número de pares de vértices {X, Y} tal que cualquier camino de X a Y contenga ambos vértices A y B .
Nota:
- { X, Y } se trata como equivalente a { Y, X }.
- X != A, X != B, Y != A e Y != B.
Ejemplos:
Para el gráfico anterior:
Entrada: A = 3, B = 5
Salida: 4
Explicación:
Hay cuatro pares { X, Y } tales que todos los caminos desde el origen X hasta el destino Y contienen los vértices A, B. Son :
{1, 6}, {1, 7}, {2, 6} y {2, 7}.
Para el gráfico anterior:
Entrada: A = 2, B = 1
Salida: 1
Explicación:
Solo hay un par { X, Y } tal que todos los caminos desde el origen X hasta el destino Y contienen los vértices A, B. Eso es:
{4, 3}.
Acercarse:
- Para el gráfico dado, si para cualquier par {X, Y} , existe algún otro camino entre ellos aparte de los vértices A y B dados , entonces esos dos vértices no están incluidos en la respuesta final. Esto se debe a que necesitamos el recuento de pares de modo que cualquier camino de esos pares consista en los vértices A y B.
- Por lo tanto, estamos interesados en pares de vértices {X, Y} tales que al eliminar el vértice A (mientras se va de B ) se rompe la conexión de X a Y y al eliminar el vértice B (mientras se va de A ) se rompe la conexión de X a y
- En otras palabras, el par {X, Y} nos interesa si X e Y pertenecen a los diferentes componentes del gráfico tanto al quitar A como al quitar B.
Por lo tanto, para encontrar los pares anteriores, se siguen los siguientes pasos:
- Considere un grafo conectado aleatorio dirigido donde algún grupo de Nodes que están interconectados está conectado a A y algún grupo de Nodes interconectados está conectado a B. A y B pueden o no tener Nodes entre ellos.
- ¿Qué pasa si eliminamos tanto A como B ? Entonces el gráfico puede desconectarse o permanecer conectado.
- Si el gráfico permanece conectado, entonces no existe ningún par de vértices porque hay otros caminos en el gráfico para todos los pares {X, Y} sin los vértices A y B en él.
- Si el gráfico se desconecta, surgen dos casos:
- Al eliminar los vértices A y B, el gráfico se convierte en dos componentes desconectadas.
- Al eliminar los vértices A y B, el gráfico se convierte en tres componentes desconectadas.
Si al quitar los vértices A y B , el grafo se convierte en dos componentes desconectadas, entonces se dan tres casos:
- Cuando hay un grupo de Nodes interconectados conectados al vértice A, algunos Nodes independientes están conectados a A y B y el vértice B es el Node hoja del gráfico:
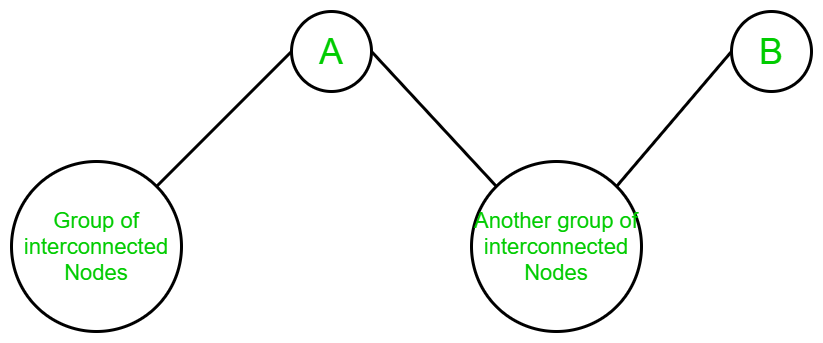
- Claramente, en el gráfico anterior, el gráfico se convierte en dos componentes diferentes cuando se eliminan el vértice A y el vértice B. Y cualquier componente puede descartarse porque los vértices de un componente pueden ir a los vértices de cualquier otro componente sin atravesar el vértice B . Entonces no existe ningún par.
- Cuando hay un grupo de Nodes interconectados conectados al vértice B, algunos Nodes independientes están conectados a A y B y el vértice A es el Node hoja del gráfico:

- Claramente, en el gráfico anterior, el gráfico se convierte en dos componentes diferentes cuando se eliminan el vértice A y el vértice B. Y cualquier componente puede descartarse porque los vértices de un componente pueden ir a los vértices de cualquier otro componente sin atravesar el vértice A . Entonces no existe ningún par.
- Cuando no hay Nodes entre el vértice A y el vértice B y ninguno de los vértices A y B son los Nodes hoja del grafo:

- Claramente, en el gráfico anterior, el gráfico se convierte en dos componentes diferentes cuando se eliminan el vértice A y el vértice B. Aquí, cualquiera de los vértices de un componente se puede emparejar con cualquier vértice del otro componente. Por lo tanto, el número de pares en este gráfico se convierte en el producto del número de Nodes interconectados en el componente 1 y el componente dos.
Si al quitar los vértices A y B, el grafo se convierte en tres componentes inconexas, entonces solo se presenta un caso:
- Cuando hay un grupo de Nodes interconectados conectados al vértice A, el vértice B y hay otro grupo de Nodes entre el vértice A y el vértice B y ninguno de los vértices A y B son los Nodes hoja:

- En este caso, la componente entre el vértice A y B puede descartarse por las razones antes mencionadas. Y, una vez descartado, es directamente el caso 3 en el gráfico de dos componentes. El mismo concepto se aplica para encontrar el número de vértices.
Por lo tanto, la idea anterior se implementa en los siguientes pasos:
- Almacene el gráfico como una lista de adyacencia utilizando el vector STL.
- Ejecute DFS de manera que arreglemos el vértice B como si lo elimináramos. Esto se puede hacer usando la condición base de la función DFS, es decir, la llamada se devuelve al llegar al vértice B.
- Cuente los vértices que A no puede alcanzar después de eliminar B .
- Repita los dos pasos anteriores fijando el vértice A y contando el número de vértices que B no puede alcanzar después de eliminar el vértice A .
- Almacene ambos conteos en dos variables diferentes. Esto representa el recuento de vértices establecidos primero al eliminar B y luego eliminar A .
- Multiplicar ambos conteos es la respuesta requerida.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find the number
// of pairs such that the path between
// every pair contains two given vertices
#include <bits/stdc++.h>
using namespace std;
int cnt, num_vertices, num_edges, a, b;
// Function to perform DFS on the given graph
// by fixing the a vertex
void dfs(int a, int b, vector<int> v[], int vis[])
{
// To mark a particular vertex as visited
vis[a] = 1;
// Variable to store the count of the
// vertices which can be reached from a
cnt++;
// Performing the DFS by iterating over
// the visited array
for (auto i : v[a]) {
// If the vertex is not visited
// and removing the vertex b
if (!vis[i] && i != b)
dfs(i, b, v, vis);
}
}
// Function to return the number of pairs
// such that path between any two pairs
// consists the given two vertices A and B
void Calculate(vector<int> v[])
{
// Initializing the visited array
// and assigning it with 0's
int vis[num_vertices + 1];
memset(vis, 0, sizeof(vis));
// Initially, the count of vertices is 0
cnt = 0;
// Performing DFS by removing the vertex B
dfs(a, b, v, vis);
// Count the vertices which cannot be
// reached after removing the vertex B
int ans1 = num_vertices - cnt - 1;
// Again reinitializing the visited array
memset(vis, 0, sizeof(vis));
// Setting the count of vertices to 0 to
// perform the DFS again
cnt = 0;
// Performing the DFS by removing the vertex A
dfs(b, a, v, vis);
// Count the vertices which cannot be
// reached after removing the vertex A
int ans2 = num_vertices - cnt - 1;
// Multiplying both the vertices set
cout << ans1 * ans2 << "\n";
}
// Driver code
int main()
{
num_vertices = 7, num_edges = 7, a = 3, b = 5;
int edges[][2] = { { 1, 2 },
{ 2, 3 },
{ 3, 4 },
{ 4, 5 },
{ 5, 6 },
{ 6, 7 },
{ 7, 5 } };
vector<int> v[num_vertices + 1];
// Loop to store the graph
for (int i = 0; i < num_edges; i++) {
v[edges[i][0]].push_back(edges[i][1]);
v[edges[i][1]].push_back(edges[i][0]);
}
Calculate(v);
return 0;
}
Java
// Java program to find the number
// of pairs such that the path between
// every pair contains two given vertices
import java.util.*;
class GFG{
static int N = 1000001;
static int c, n, m, a, b;
// Function to perform DFS on the given graph
// by fixing the a vertex
static void dfs(int a, int b, Vector<Integer> v[], int vis[])
{
// To mark a particular vertex as visited
vis[a] = 1;
// Variable to store the count of the
// vertices which can be reached from a
c++;
// Performing the DFS by iterating over
// the visited array
for (int i : v[a]) {
// If the vertex is not visited
// and removing the vertex b
if (vis[i] == 0 && i != b)
dfs(i, b, v, vis);
}
}
// Function to return the number of pairs
// such that path between any two pairs
// consists of the given two vertices A and B
static void Calculate(Vector<Integer> v[])
{
// Initializing the visited array
// and assigning it with 0's
int []vis = new int[n + 1];
Arrays.fill(vis, 0);
// Initially, the count of vertices is 0
c = 0;
// Performing DFS by removing the vertex B
dfs(a, b, v, vis);
// Count the vertices which cannot be
// reached after removing the vertex B
int ans1 = n - c - 1;
// Again reinitializing the visited array
Arrays.fill(vis, 0);
// Setting the count of vertices to 0 to
// perform the DFS again
c = 0;
// Performing the DFS by removing the vertex A
dfs(b, a, v, vis);
// Count the vertices which cannot be
// reached after removing the vertex A
int ans2 = n - c - 1;
// Multiplying both the vertices set
System.out.print(ans1 * ans2+ "\n");
}
// Driver code
public static void main(String[] args)
{
n = 7;
m = 7;
a = 3;
b = 5;
int edges[][] = { { 1, 2 },
{ 2, 3 },
{ 3, 4 },
{ 4, 5 },
{ 5, 6 },
{ 6, 7 },
{ 7, 5 } };
Vector<Integer> []v = new Vector[n + 1];
for(int i= 0; i <= n; i++) {
v[i] = new Vector<Integer>();
}
// Loop to store the graph
for (int i = 0; i < m; i++) {
v[edges[i][0]].add(edges[i][1]);
v[edges[i][1]].add(edges[i][0]);
}
Calculate(v);
}
}
// This code is contributed by Rajput-Ji
Python3
# Python 3 program to find the number # of pairs such that the path between # every pair contains two given vertices N = 1000001 c = 0 n = 0 m = 0 a = 0 b = 0 # Function to perform DFS on the given graph # by fixing the a vertex def dfs(a,b,v,vis): global c # To mark a particular vertex as visited vis[a] = 1 # Variable to store the count of the # vertices which can be reached from a c += 1 # Performing the DFS by iterating over # the visited array for i in v[a]: # If the vertex is not visited # and removing the vertex b if (vis[i]==0 and i != b): dfs(i, b, v, vis) # Function to return the number of pairs # such that path between any two pairs # consists of the given two vertices A and B def Calculate(v): global c # Initializing the visited array # and assigning it with 0's vis = [0 for i in range(n + 1)] # Initially, the count of vertices is 0 c = 0 # Performing DFS by removing the vertex B dfs(a, b, v, vis) # Count the vertices which cannot be # reached after removing the vertex B ans1 = n - c - 1 # Again reinitializing the visited array vis = [0 for i in range(len(vis))] # Setting the count of vertices to 0 to # perform the DFS again c = 0 # Performing the DFS by removing the vertex A dfs(b, a, v, vis) # Count the vertices which cannot be # reached after removing the vertex A ans2 = n - c - 1 # Multiplying both the vertices set print(ans1 * ans2) # Driver code if __name__ == '__main__': n = 7 m = 7 a = 3 b = 5 edges = [[1, 2], [2, 3], [3, 4], [4, 5], [5, 6], [6, 7], [7, 5]] v = [[] for i in range(n + 1)] # Loop to store the graph for i in range(m): v[edges[i][0]].append(edges[i][1]) v[edges[i][1]].append(edges[i][0]) Calculate(v) # This code is contributed by Surendra_Gangwar
C#
// C# program to find the number
// of pairs such that the path between
// every pair contains two given vertices
using System;
using System.Collections.Generic;
class GFG{
static int N = 1000001;
static int c, n, m, a, b;
// Function to perform DFS on the given graph
// by fixing the a vertex
static void dfs(int a, int b, List<int> []v, int []vis)
{
// To mark a particular vertex as visited
vis[a] = 1;
// Variable to store the count of the
// vertices which can be reached from a
c++;
// Performing the DFS by iterating over
// the visited array
foreach (int i in v[a]) {
// If the vertex is not visited
// and removing the vertex b
if (vis[i] == 0 && i != b)
dfs(i, b, v, vis);
}
}
// Function to return the number of pairs
// such that path between any two pairs
// consists of the given two vertices A and B
static void Calculate(List<int> []v)
{
// Initializing the visited array
// and assigning it with 0's
int []vis = new int[n + 1];
for(int i = 0; i < n + 1; i++)
vis[i] = 0;
// Initially, the count of vertices is 0
c = 0;
// Performing DFS by removing the vertex B
dfs(a, b, v, vis);
// Count the vertices which cannot be
// reached after removing the vertex B
int ans1 = n - c - 1;
// Again reinitializing the visited array
for(int i = 0; i < n + 1; i++)
vis[i] = 0;
// Setting the count of vertices to 0 to
// perform the DFS again
c = 0;
// Performing the DFS by removing the vertex A
dfs(b, a, v, vis);
// Count the vertices which cannot be
// reached after removing the vertex A
int ans2 = n - c - 1;
// Multiplying both the vertices set
Console.Write(ans1 * ans2+ "\n");
}
// Driver code
public static void Main(String[] args)
{
n = 7;
m = 7;
a = 3;
b = 5;
int [,]edges = { { 1, 2 },
{ 2, 3 },
{ 3, 4 },
{ 4, 5 },
{ 5, 6 },
{ 6, 7 },
{ 7, 5 } };
List<int> []v = new List<int>[n + 1];
for(int i= 0; i <= n; i++) {
v[i] = new List<int>();
}
// Loop to store the graph
for (int i = 0; i < m; i++) {
v[edges[i,0]].Add(edges[i,1]);
v[edges[i,1]].Add(edges[i,0]);
}
Calculate(v);
}
}
// This code is contributed by Princi Singh
Javascript
<script>
// Javascript program to find the number
// of pairs such that the path between
// every pair contains two given vertices
let N = 1000001;
let c, n, m, a, b;
// Function to perform DFS on the given graph
// by fixing the a vertex
function dfs(a, b, v, vis)
{
// To mark a particular vertex as visited
vis[a] = 1;
// Variable to store the count of the
// vertices which can be reached from a
c++;
// Performing the DFS by iterating over
// the visited array
for(let i of v[a]) {
// If the vertex is not visited
// and removing the vertex b
if (vis[i] == 0 && i != b)
dfs(i, b, v, vis);
}
}
// Function to return the number of pairs
// such that path between any two pairs
// consists of the given two vertices A and B
function Calculate(v)
{
// Initializing the visited array
// and assigning it with 0's
let vis = new Array(n + 1);
for(let i = 0; i < n + 1; i++)
vis[i] = 0;
// Initially, the count of vertices is 0
c = 0;
// Performing DFS by removing the vertex B
dfs(a, b, v, vis);
// Count the vertices which cannot be
// reached after removing the vertex B
let ans1 = n - c - 1;
// Again reinitializing the visited array
for(let i = 0; i < n + 1; i++)
vis[i] = 0;
// Setting the count of vertices to 0 to
// perform the DFS again
c = 0;
// Performing the DFS by removing the vertex A
dfs(b, a, v, vis);
// Count the vertices which cannot be
// reached after removing the vertex A
let ans2 = n - c - 1;
// Multiplying both the vertices set
document.write((ans1 * ans2)+ "</br>");
}
n = 7;
m = 7;
a = 3;
b = 5;
let edges = [ [ 1, 2 ],
[ 2, 3 ],
[ 3, 4 ],
[ 4, 5 ],
[ 5, 6 ],
[ 6, 7 ],
[ 7, 5 ] ];
let v = new Array(n + 1);
for(let i= 0; i <= n; i++) {
v[i] = [];
}
// Loop to store the graph
for (let i = 0; i < m; i++) {
v[edges[i][0]].push(edges[i][1]);
v[edges[i][1]].push(edges[i][0]);
}
Calculate(v);
// This code is contributed by divyeshrabadiya07.
</script>
4
Análisis de Complejidad de Tiempo:
- Aquí, DFS se realiza dos veces. Por lo tanto, la complejidad temporal total es O(V + E) .
Espacio Auxiliar : O(V + E)
Publicación traducida automáticamente
Artículo escrito por sharadgoyal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

