Dada una string que consta de números enteros del 0 al 9. La tarea es contar el número de substrings que, cuando se convierten en enteros, son divisibles por 6. La substring no contiene ceros a la izquierda. Ejemplos:
Input : s = "606". Output : 5 Substrings "6", "0", "6", "60", "606" are divisible by 6. Input : s = "4806". Output : 5 "0", "6", "48", "480", "4806" are substring which are divisible by 6.
Método 1: (Fuerza bruta) La idea es encontrar todas las substrings de la string dada y verificar si la substring es divisible por 6 o no .
Complejidad Temporal: O(n 2 ).
Método 2: (Programación dinámica) Como se discutió en Comprobar si un número grande es divisible por 6 o no . Un número es divisible por 6 si el último dígito es divisible por 2 y la suma de los dígitos es divisible por 3. La idea es usar la programación dinámica, que nos permite calcular la respuesta de manera rápida y eficiente al rastrear las respuestas calculadas previamente y usar estas respuestas almacenadas en su lugar. de recalcular valores.
Sea f(i, m) el número de strings que comienzan en el índice i y la suma de sus dígitos módulo 3 (hasta ahora) es my el número que representa es par . Entonces, nuestra respuesta sería 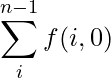
Sea x el i -ésimo dígito de la string. De f(i, m) necesitamos encontrar todas las substrings pares que comienzan en i + 1. Además, obtendremos una substring extra si (x + m) es divisible por 3 y x es par. Entonces, obtenemos la relación de recurrencia
// We initially pass m (sum modulo 3 so far) as 0
f(i, m) = ((x + m)%3 == 0 and x%2 == 0) +
f(i + 1, (m + x)%3) // Recursive
Al memorizar los estados, obtenemos la solución O(n). A continuación se muestra la implementación de este enfoque:
C++
// C++ program to calculate number of substring
// divisible by 6.
#include <bits/stdc++.h>
#define MAX 100002
using namespace std;
// Return the number of substring divisible by 6
// and starting at index i in s[] and previous sum
// of digits modulo 3 is m.
int f(int i, int m, char s[], int memoize[][3])
{
// End of the string.
if (i == strlen(s))
return 0;
// If already calculated, return the
// stored value.
if (memoize[i][m] != -1)
return memoize[i][m];
// Converting into integer.
int x = s[i] - '0';
// Increment result by 1, if current digit
// is divisible by 2 and sum of digits is
// divisible by 3.
// And recur for next index with new modulo.
int ans = ((x+m)%3 == 0 && x%2 == 0) +
f(i+1, (m+x)%3, s, memoize);
return memoize[i][m] = ans;
}
// Returns substrings divisible by 6.
int countDivBy6(char s[])
{
int n = strlen(s);
// For storing the value of all states.
int memoize[n+1][3];
memset(memoize, -1, sizeof memoize);
int ans = 0;
for (int i = 0; i < strlen(s); i++)
{
// If string contain 0, increment count by 1.
if (s[i] == '0')
ans++;
// Else calculate using recursive function.
// Pass previous sum modulo 3 as 0.
else
ans += f(i, 0, s, memoize);
}
return ans;
}
// Driven Program
int main()
{
char s[] = "4806";
cout << countDivBy6(s) << endl;
return 0;
}
Java
// Java program to calculate number of substring
// divisible by 6.
import java.util.*;
class GFG
{
static int MAX = 100002;
// Return the number of substring divisible by 6
// and starting at index i in s[] and previous sum
// of digits modulo 3 is m.
static int f(int i, int m, char s[], int memoize[][])
{
// End of the string.
if (i == s.length)
{
return 0;
}
// If already calculated, return the
// stored value.
if (memoize[i][m] != -1)
{
return memoize[i][m];
}
// Converting into integer.
int x = s[i] - '0';
// Increment result by 1, if current digit
// is divisible by 2 and sum of digits is
// divisible by 3.
// And recur for next index with new modulo.
int ans = ((x + m) % 3 == 0 && x % 2 == 0) ? 1 + f(i + 1,
(m + x) % 3, s, memoize) : f(i + 1, (m + x) % 3, s, memoize);
memoize[i][m] = ans;
return memoize[i][m];
}
// Returns substrings divisible by 6.
static int countDivBy6(char s[])
{
int n = s.length;
// For storing the value of all states.
int[][] memoize = new int[n + 1][3];
for (int i = 0; i < n + 1; i++)
{
for (int j = 0; j < 3; j++)
{
memoize[i][j] = -1;
}
}
int ans = 0;
for (int i = 0; i < s.length; i++)
{
// If string contain 0, increment count by 1.
if (s[i] == '0')
{
ans++;
}
// Else calculate using recursive function.
// Pass previous sum modulo 3 as 0.
else
{
ans += f(i, 0, s, memoize);
}
}
return ans;
}
// Driven Program
public static void main(String[] args)
{
char s[] = "4806".toCharArray();
System.out.println(countDivBy6(s));
}
}
// This code is contributed by Rajput-Ji
Python3
# Python3 program to calculate number
# of substring
# Return the number of substring divisible
# by 6 and starting at index i in s[] and
# previous sum of digits modulo 3 is m.
def f(i, m, s, memoize):
# End of the string.
if (i == len(s)):
return 0
# If already calculated, return
# the stored value.
if (memoize[i][m] != -1):
return memoize[i][m]
# Converting into integer.
x = ord(s[i]) - ord('0')
# Increment result by 1, if current digit
# is divisible by 2 and sum of digits is
# divisible by 3.
# And recur for next index with new modulo.
ans = (((x + m) % 3 == 0 and x % 2 == 0) +
f(i + 1, (m + x) % 3, s, memoize))
memoize[i][m] = ans
return memoize[i][m]
# Returns substrings divisible by 6.
def countDivBy6(s):
n = len(s)
# For storing the value of all states.
memoize = [[-1] * 3 for i in range(n + 1)]
ans = 0
for i in range(len(s)):
# If string contain 0, increment
# count by 1.
if (s[i] == '0'):
ans += 1
# Else calculate using recursive function.
# Pass previous sum modulo 3 as 0.
else:
ans += f(i, 0, s, memoize)
return ans
# Driver Code
if __name__ == '__main__':
s = "4806"
print(countDivBy6(s))
# This code is contributed by PranchalK
C#
// C# program to calculate number of substring
// divisible by 6.
using System;
class GFG
{
static int MAX = 100002;
// Return the number of substring divisible by 6
// and starting at index i in s[] and previous sum
// of digits modulo 3 is m.
static int f(int i, int m, char []s, int [,]memoize)
{
// End of the string.
if (i == s.Length)
{
return 0;
}
// If already calculated, return the
// stored value.
if (memoize[i,m] != -1)
{
return memoize[i,m];
}
// Converting into integer.
int x = s[i] - '0';
// Increment result by 1, if current digit
// is divisible by 2 and sum of digits is
// divisible by 3.
// And recur for next index with new modulo.
int ans = ((((x + m) % 3 == 0) && (x % 2 == 0)) ? 1 : 0)
+ f(i + 1, (m + x) % 3, s, memoize);
return memoize[i,m] = ans;
}
// Returns substrings divisible by 6.
static int countDivBy6(char []s)
{
int n = s.Length;
// For storing the value of all states.
int[,] memoize = new int[n + 1,3];
for (int i = 0; i < n + 1; i++)
{
for (int j = 0; j < 3; j++)
{
memoize[i,j] = -1;
}
}
int ans = 0;
for (int i = 0; i < s.Length; i++)
{
// If string contain 0, increment count by 1.
if (s[i] == '0')
{
ans++;
}
// Else calculate using recursive function.
// Pass previous sum modulo 3 as 0.
else
{
ans += f(i, 0, s, memoize);
}
}
return ans;
}
// Driver code
public static void Main(String[] args)
{
char []s = "4806".ToCharArray();
Console.WriteLine(countDivBy6(s));
}
}
/* This code is contributed by PrinciRaj1992 */
Javascript
<script>
// JavaScript program to calculate number
// of substring
// Return the number of substring divisible
// by 6 and starting at index i in s[] and
// previous sum of digits modulo 3 is m.
function f(i, m, s, memoize){
// End of the string.
if (i == s.length)
return 0
// If already calculated, return
// the stored value.
if (memoize[i][m] != -1)
return memoize[i][m]
// Converting into integer.
let x = s.charCodeAt(i) - '0'.charCodeAt(0)
// Increment result by 1, if current digit
// is divisible by 2 and sum of digits is
// divisible by 3.
// And recur for next index with new modulo.
ans = (((x + m) % 3 == 0 && x % 2 == 0) + f(i + 1, (m + x) % 3, s, memoize))
memoize[i][m] = ans
return memoize[i][m]
}
// Returns substrings divisible by 6.
function countDivBy6(s){
let n = s.length
// For storing the value of all states.
let memoize = new Array(n + 1)
for(let i=0;i<n + 1;i++){
memoize[i] = new Array(3).fill(-1)
}
let ans = 0
for(let i=0;i<s.length;i++){
// If string contain 0, increment
// count by 1.
if (s[i] == '0')
ans += 1
// Else calculate using recursive function.
// Pass previous sum modulo 3 as 0.
else
ans += f(i, 0, s, memoize)
}
return ans
}
// Driver Code
let s = "4806"
document.write(countDivBy6(s))
// This code is contributed by shinjanpatra
</script>
5
Complejidad temporal: O(n).
Espacio Auxiliar: O(n)
Este artículo es una contribución de Aarti_Rathi y Anuj Chauhan . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA