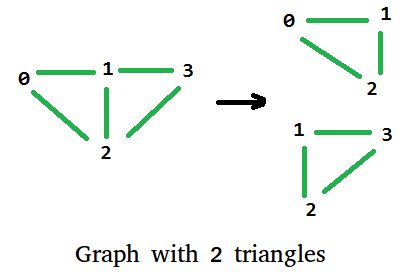
Dado un gráfico simple no dirigido, necesitamos encontrar cuántos triángulos puede tener. Por ejemplo, el siguiente gráfico tiene 2 triángulos.
C++
// A C++ program for finding
// number of triangles in an
// Undirected Graph. The program
// is for adjacency matrix
// representation of the graph
#include <bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 4
// Utility function for matrix
// multiplication
void multiply(int A[][V], int B[][V], int C[][V])
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
C[i][j] = 0;
for (int k = 0; k < V; k++)
C[i][j] += A[i][k]*B[k][j];
}
}
}
// Utility function to calculate
// trace of a matrix (sum of
// diagonal elements)
int getTrace(int graph[][V])
{
int trace = 0;
for (int i = 0; i < V; i++)
trace += graph[i][i];
return trace;
}
// Utility function for calculating
// number of triangles in graph
int triangleInGraph(int graph[][V])
{
// To Store graph^2
int aux2[V][V];
// To Store graph^3
int aux3[V][V];
// Initialising aux
// matrices with 0
for (int i = 0; i < V; ++i)
for (int j = 0; j < V; ++j)
aux2[i][j] = aux3[i][j] = 0;
// aux2 is graph^2 now printMatrix(aux2);
multiply(graph, graph, aux2);
// after this multiplication aux3 is
// graph^3 printMatrix(aux3);
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
}
// driver code
int main()
{
int graph[V][V] = {{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}
};
printf("Total number of Triangle in Graph : %d\n",
triangleInGraph(graph));
return 0;
}
Java
// Java program to find number
// of triangles in an Undirected
// Graph. The program is for
// adjacency matrix representation
// of the graph
import java.io.*;
class Directed
{
// Number of vertices in
// the graph
int V = 4;
// Utility function for
// matrix multiplication
void multiply(int A[][], int B[][],
int C[][])
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
C[i][j] = 0;
for (int k = 0; k < V;
k++)
{
C[i][j] += A[i][k]*
B[k][j];
}
}
}
}
// Utility function to calculate
// trace of a matrix (sum of
// diagonal elements)
int getTrace(int graph[][])
{
int trace = 0;
for (int i = 0; i < V; i++)
{
trace += graph[i][i];
}
return trace;
}
// Utility function for
// calculating number of
// triangles in graph
int triangleInGraph(int graph[][])
{
// To Store graph^2
int[][] aux2 = new int[V][V];
// To Store graph^3
int[][] aux3 = new int[V][V];
// Initialising aux matrices
// with 0
for (int i = 0; i < V; ++i)
{
for (int j = 0; j < V; ++j)
{
aux2[i][j] = aux3[i][j] = 0;
}
}
// aux2 is graph^2 now
// printMatrix(aux2)
multiply(graph, graph, aux2);
// after this multiplication aux3
// is graph^3 printMatrix(aux3)
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
}
// Driver code
public static void main(String args[])
{
Directed obj = new Directed();
int graph[][] = { {0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}
};
System.out.println("Total number of Triangle in Graph : "+
obj.triangleInGraph(graph));
}
}
// This code is contributed by Anshika Goyal.
Python3
# A Python3 program for finding number of
# triangles in an Undirected Graph. The
# program is for adjacency matrix
# representation of the graph
# Utility function for matrix
# multiplication
def multiply(A, B, C):
global V
for i in range(V):
for j in range(V):
C[i][j] = 0
for k in range(V):
C[i][j] += A[i][k] * B[k][j]
# Utility function to calculate
# trace of a matrix (sum of
# diagonal elements)
def getTrace(graph):
global V
trace = 0
for i in range(V):
trace += graph[i][i]
return trace
# Utility function for calculating
# number of triangles in graph
def triangleInGraph(graph):
global V
# To Store graph^2
aux2 = [[None] * V for i in range(V)]
# To Store graph^3
aux3 = [[None] * V for i in range(V)]
# Initialising aux
# matrices with 0
for i in range(V):
for j in range(V):
aux2[i][j] = aux3[i][j] = 0
# aux2 is graph^2 now printMatrix(aux2)
multiply(graph, graph, aux2)
# after this multiplication aux3 is
# graph^3 printMatrix(aux3)
multiply(graph, aux2, aux3)
trace = getTrace(aux3)
return trace // 6
# Driver Code
# Number of vertices in the graph
V = 4
graph = [[0, 1, 1, 0],
[1, 0, 1, 1],
[1, 1, 0, 1],
[0, 1, 1, 0]]
print("Total number of Triangle in Graph :",
triangleInGraph(graph))
# This code is contributed by PranchalK
C#
// C# program to find number
// of triangles in an Undirected
// Graph. The program is for
// adjacency matrix representation
// of the graph
using System;
class GFG
{
// Number of vertices
// in the graph
int V = 4;
// Utility function for
// matrix multiplication
void multiply(int [,]A, int [,]B,
int [,]C)
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
C[i, j] = 0;
for (int k = 0; k < V;
k++)
{
C[i, j] += A[i, k]*
B[k, j];
}
}
}
}
// Utility function to
// calculate trace of
// a matrix (sum of
// diagonal elements)
int getTrace(int [,]graph)
{
int trace = 0;
for (int i = 0; i < V; i++)
{
trace += graph[i, i];
}
return trace;
}
// Utility function for
// calculating number of
// triangles in graph
int triangleInGraph(int [,]graph)
{
// To Store graph^2
int[,] aux2 = new int[V, V];
// To Store graph^3
int[,] aux3 = new int[V, V];
// Initialising aux matrices
// with 0
for (int i = 0; i < V; ++i)
{
for (int j = 0; j < V; ++j)
{
aux2[i, j] = aux3[i, j] = 0;
}
}
// aux2 is graph^2 now
// printMatrix(aux2)
multiply(graph, graph, aux2);
// after this multiplication aux3
// is graph^3 printMatrix(aux3)
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
}
// Driver code
public static void Main()
{
GFG obj = new GFG();
int [,]graph = {{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}};
Console.WriteLine("Total number of " +
"Triangle in Graph : "+
obj.triangleInGraph(graph));
}
}
// This code is contributed by anuj_67.
Javascript
<script>
// Javascript program to find number
// of triangles in an Undirected
// Graph. The program is for
// adjacency matrix representation
// of the graph
// Number of vertices in the graph
let V = 4;
// Utility function for matrix
// multiplication
function multiply(A, B, C)
{
for(let i = 0; i < V; i++)
{
for(let j = 0; j < V; j++)
{
C[i][j] = 0;
for(let k = 0; k < V; k++)
C[i][j] += A[i][k] * B[k][j];
}
}
}
// Utility function to calculate
// trace of a matrix (sum of
// diagonal elements)
function getTrace(graph)
{
let trace = 0;
for(let i = 0; i < V; i++)
trace += graph[i][i];
return trace;
}
// Utility function for calculating
// number of triangles in graph
function triangleInGraph(graph)
{
// To Store graph^2
let aux2 = new Array(V);
// To Store graph^3
let aux3 = new Array(V);
// Initialising aux
// matrices with 0
for(let i = 0; i < V; ++i)
{
aux2[i] = new Array(V);
aux3[i] = new Array(V);
for(let j = 0; j < V; ++j)
{
aux2[i][j] = aux3[i][j] = 0;
}
}
// aux2 is graph^2 now printMatrix(aux2);
multiply(graph, graph, aux2);
// After this multiplication aux3 is
// graph^3 printMatrix(aux3);
multiply(graph, aux2, aux3);
let trace = getTrace(aux3);
return (trace / 6);
}
// Driver code
let graph = [ [ 0, 1, 1, 0 ],
[ 1, 0, 1, 1 ],
[ 1, 1, 0, 1 ],
[ 0, 1, 1, 0 ] ];
document.write("Total number of Triangle in Graph : " +
triangleInGraph(graph));
// This code is contributed by divyesh072019
</script>
C++
#include<iostream>
#include<string>
#include<algorithm>
#include<cstring>
#include<vector>
#include<bitset>
using namespace std;
#define V 4
int main()
{
// Graph represented as adjacency matrix
int graph[][V] = {{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}};
// create the adjacency list of the graph (as bit masks)
// set the bits at positions [i][j] & [j][i] to 1, if there is an undirected edge between i and j
vector<bitset<V>> Bitset_Adj_List(V);
for (int i = 0; i < V;i++)
for (int j = 0; j < V;j++)
if(graph[i][j])
Bitset_Adj_List[i][j] = 1,
Bitset_Adj_List[j][i] = 1;
int ans = 0;
for (int i = 0; i < V;i++)
for (int j = 0; j < V;j++)
// if i & j are adjacent
// compute the number of nodes that are adjacent to i & j
if(Bitset_Adj_List[i][j] == 1 && i != j){
bitset<V> Mask = Bitset_Adj_List[i] & Bitset_Adj_List[j];
ans += Mask.count();
}
// divide the answer by 6 to avoid duplicates
ans /= 6;
cout << "The number of Triangles in the Graph is : " << ans;
// This code is contributed
// by Gatea David
}
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA