Número máximo de aristas que el gráfico de N vértices puede tener de modo que el gráfico no tenga triángulos | Teorema de Mantel

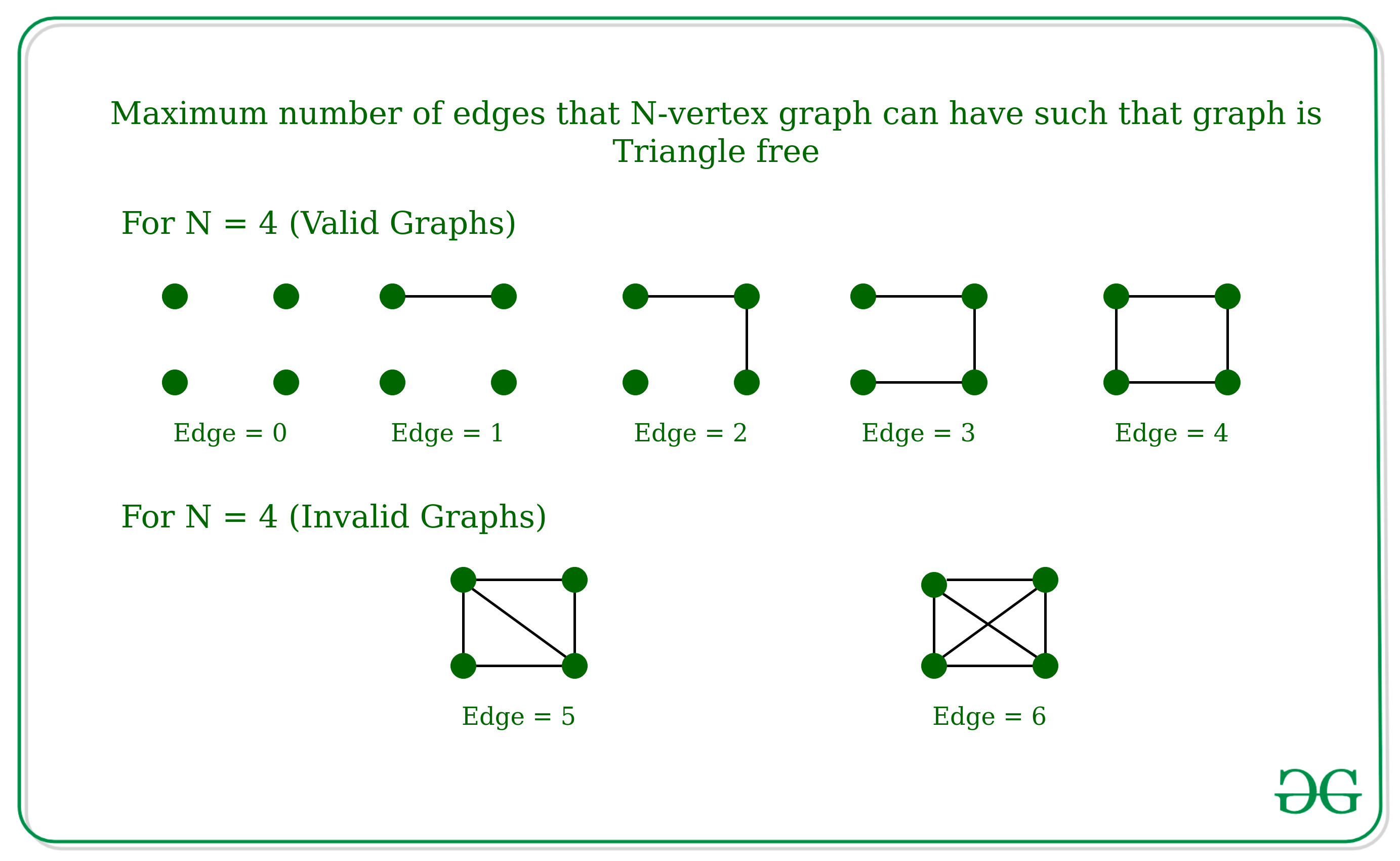
Dado un número N , que es el número de Nodes en un gráfico, la tarea es encontrar el número máximo de aristas que puede tener un gráfico de N vértices de modo que el gráfico no tenga triángulos (lo que significa que no debe haber tres aristas A, B, C en el gráfico tal que A está conectado a B, B está conectado a C y C está conectado a A). El gráfico no puede contener un bucle automático o varios bordes.

Ejemplos: 

Entrada: N = 4 
Salida: 4 
Explicación: 
 

Entrada: N = 3 
Salida: 2 
Explicación: 
Si hay tres aristas en un gráfico de 3 vértices, entonces tendrá un triángulo. 
 

Enfoque: este problema se puede resolver utilizando el teorema de Mantel , que establece que el número máximo de aristas en un gráfico que no contiene ningún triángulo es piso (n ² /4). En otras palabras, se debe eliminar casi la mitad de los bordes para obtener un gráfico sin triángulos.

¿Cómo funciona el teorema de Mantel?  
Para cualquier gráfico , tal que el gráfico no tenga triángulos, entonces para cualquier vértice Z solo se puede conectar a cualquiera de los vértices de x e y, es decir, para cualquier borde conectado entre x e y, d(x) + d(y) ≤ N, donde d(x) y d(y) es el grado del vértice x e y.  

• Entonces, el Grado de todos los vértices – 
   

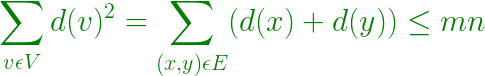
• Por la desigualdad de Cauchy-Schwarz – 
   

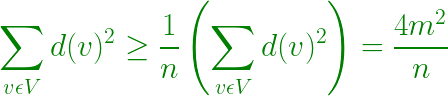
• Por lo tanto, 4m ² / n ≤ mn, lo que implica m ≤ n ² / 4 

A continuación se muestra la implementación del enfoque anterior: 

// C++ implementation to find the maximum
// number of edges for triangle free graph
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the maximum number of
// edges in a N-vertex graph.
int solve(int n)
{
    // According to the Mantel's theorem
    // the maximum number of edges will be
    // floor of [(n^2)/4]
    int ans = (n * n / 4);
 
    return ans;
}
 
// Driver Function
int main()
{
    int n = 10;
    cout << solve(n) << endl;
    return 0;
}

// Java implementation to find the maximum
// number of edges for triangle free graph
class GFG
{
 
    // Function to find the maximum number of
    // edges in a N-vertex graph.
    public static int solve(int n)
    {
         
        // According to the Mantel's theorem
        // the maximum number of edges will be
        // floor of [(n^2)/4]
        int ans = (n * n / 4);
 
        return ans;
    }
 
    // Driver code
    public static void main(String args[])
    {
        int n = 10;
        System.out.println(solve(n));
    }
}
 
// This code is contributed by divyamohan123

// C# implementation to find the maximum
// number of edges for triangle free graph
using System;
 
class GFG
{
 
    // Function to find the maximum number of
    // edges in a N-vertex graph.
    public static int solve(int n)
    {
         
        // According to the Mantel's theorem
        // the maximum number of edges will be
        // floor of [(n^2)/4]
        int ans = (n * n / 4);
 
        return ans;
    }
 
    // Driver code
    public static void Main()
    {
        int n = 10;
        Console.WriteLine(solve(n));
    }
}
 
// This code is contributed by AnkitRai01

# Python3 implementation to find the maximum
# number of edges for triangle free graph
 
# Function to find the maximum number of
# edges in a N-vertex graph.
def solve(n):
     
    # According to the Mantel's theorem
    # the maximum number of edges will be
    # floor of [(n^2)/4]
    ans = (n * n // 4)
 
    return ans
 
# Driver Function
if __name__ == '__main__':
    n = 10
    print(solve(n))
 
# This code is contributed by mohit kumar 29

<script>
 
// Javascript implementation to find the maximum
// number of edges for triangle free graph
 
// Function to find the maximum number of
// edges in a N-vertex graph.
function solve(n)
{
     
    // According to the Mantel's theorem
    // the maximum number of edges will be
    // floor of [(n^2)/4]
    var ans = (n * n / 4);
 
    return ans;
}
 
// Driver code
var n = 10;
 
document.write(solve(n));
 
// This code is contributed by aashish1995
 
</script>

25

Complejidad de tiempo: O(1)