Número máximo de regiones en las que N rectas no paralelas pueden dividir un plano

Dado N ‘, el número de líneas no paralelas. La tarea es encontrar el número máximo de regiones en las que estas líneas pueden dividir un plano.
Ejemplos: 
 

Entrada: N = 3 
Salida: 7
Entrada: N = 2 
Salida: 4 
 

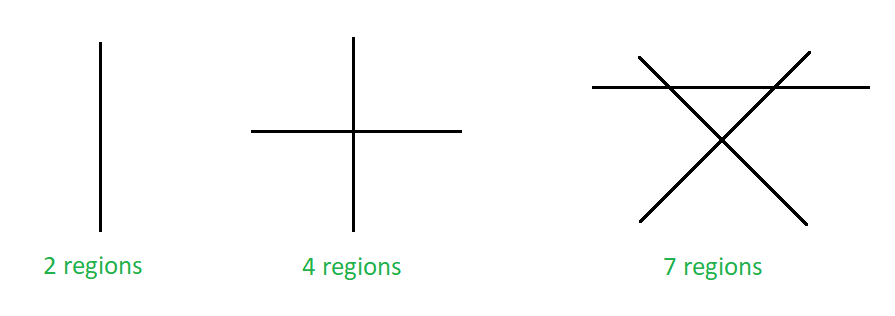
Número máximo de regiones en un plano formadas por líneas no paralelas

Enfoque: La imagen de arriba muestra el número máximo de regiones que una línea puede dividir un plano. Una recta puede dividir un plano en dos regiones, dos rectas no paralelas pueden dividir un plano en 4 regiones y tres rectas no paralelas pueden dividirlo en 7 regiones, y así sucesivamente. Cuando la n- ^ésima línea se agrega a un grupo de (n-1) líneas, el número máximo de regiones adicionales formadas es igual a n.
Ahora resuelve la recursividad de la siguiente manera: 
 

L(2) – L(1) = 2 … (i) 
L(3) – L(2) = 3 … (ii) 
L(4) – L(3) = 4 … (iii) 
. . . 
. . . 
L(n) – L(n-1) = n ; … (n) 
Sumando toda la ecuación anterior obtenemos,
L(n) – L(1) = 2 + 3 + 4 + 5 + 6 + 7 + …… + n ; 
L(n) = L(1) + 2 + 3 + 4 + 5 + 6 + 7 + …… + n ; 
L(n) = 2 + 2 + 3 + 4 + 5 + 6 + 7 + …… + n ; 
L(n) = 1 + 2 + 3 + 4 + 5 + 6 + 7 + …… + n + 1 ; 
L(n) = norte ( norte + 1 ) / 2 + 1 ;
 

El número de regiones en las que N rectas no paralelas pueden dividir un plano es igual a N*( N + 1 )/2 + 1 .
A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program to implement the above problem
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the maximum
// number of regions on a plane
void maxRegions(int n)
{
    int num;
    num = n * (n + 1) / 2 + 1;
 
    // print the maximum number of regions
    cout << num;
}
 
// Driver code
int main()
{
    int n = 10;
 
    maxRegions(n);
 
    return 0;
}

// Java program to implement the above problem
class GFG
{
 
    // Function to find the maximum
    // number of regions on a plane
    static void maxRegions(int n)
    {
        int num;
        num = n * (n + 1) / 2 + 1;
 
        // print the maximum number of regions
        System.out.println(num);;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 10;
        maxRegions(n);
    }
}
 
// This code is contributed by 29AjayKumar

# Python3 program to implement
# the above problem
 
# Function to find the maximum
# number of regions on a plane
def maxRegions(n):
    num = n * (n + 1) // 2 + 1
 
    # print the maximum number
    # of regions
    print(num)
 
# Driver code
n = 10
 
maxRegions(n)
 
# This code is contributed
# by Mohit Kumar

// C# program to implement the above problem
using System;
     
class GFG
{
 
    // Function to find the maximum
    // number of regions on a plane
    static void maxRegions(int n)
    {
        int num;
        num = n * (n + 1) / 2 + 1;
 
        // print the maximum number of regions
        Console.WriteLine(num);
    }
 
    // Driver code
    public static void Main(String[] args)
    {
        int n = 10;
        maxRegions(n);
    }
}
 
// This code is contributed by 29AjayKumar

<script>
 
// Javascript program to implement the above problem
 
// Function to find the maximum
// number of regions on a plane
function maxRegions(n)
{
    let num;
    num = parseInt( n * (n + 1) / 2) + 1;
 
    // print the maximum number of regions
    document.write(num);
}
 
// Driver code
    let n = 10;
 
    maxRegions(n);
 
</script>

56

Complejidad de tiempo : O(1)

Complejidad espacial : O (1) ya que usa variables constantes