Número mínimo de cerdos necesarios para encontrar el cubo venenoso

Dado un número entero N que indica el número de cubos, y un número entero M , que indica el tiempo mínimo en minutos que tarda un cerdo en morir después de beber veneno, la tarea es encontrar el número mínimo de cerdos necesarios para averiguar qué cubo es venenoso dentro de P minutos, si hay exactamente un balde con veneno, mientras que el resto está lleno de agua.

Ejemplos:

Entrada: N = 1000, M = 15, P = 60
Salida: 5
Explicación: El número mínimo de cerdos necesarios para encontrar el balde venenoso es 5.

Entrada: N = 4, M = 15, P = 15
Salida: 2
Explicación: El número mínimo de cerdos necesarios para encontrar el balde venenoso es 2.

Enfoque: El problema dado se puede resolver usando las observaciones dadas:

• Se puede permitir que un cerdo beba simultáneamente en tantos cubos como quiera, y la alimentación no toma tiempo.
• Después de que un cerdo haya terminado instantáneamente de beber cubos, debe haber un tiempo de inactividad por enfriamiento de M minutos. Durante este tiempo, solo se permite la observación y ninguna alimentación.
• Cualquier balde dado puede ser muestreado un número infinito de veces (por un número ilimitado de cerdos).

Ahora, P minutos para probar y M minutos para morir simplemente indican cuántas rondas se pueden usar los cerdos, es decir, cuántas veces puede comer un cerdo. Por lo tanto, declare una variable llamada r = P(Minutes To Test) / M(Minutes To Die) .

Considere los casos para comprender el enfoque:

Caso 1: Si r = 1, es decir, el número de vueltas es 1 .
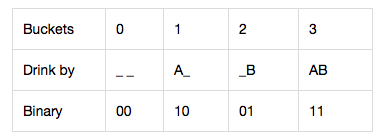
Ejemplo: 4 cubos, 15 minutos para morir y 15 minutos para probar. La respuesta es 2. Supongamos que A y B representan 2 cerdos, entonces los casos son:

Obviamente, usando la forma binaria para representar la solución como:

Conclusión: si hay x cerdos, pueden representar (codificar) 2 ^x baldes.

Caso 2: Si r > 1, es decir, el número de rondas es mayor que 1 . Sean a continuación las siguientes notaciones:

• 0 significa que el cerdo no bebe y muere.
• 1 significa que el cerdo bebe en la primera (y única) ronda.

Generalizando los resultados anteriores ( t significa que el cerdo bebe en la ronda t y muere): si hay t intentos, se usa un número basado en (t + 1) para representar (codificar) los baldes. (Esa es también la razón por la cual la primera conclusión usa el número basado en 2)

Ejemplo: 8 cubos, 15 cubos para morir y 40 cubos para probar. Ahora, hay 2(= (40/15).piso)intentos, como resultado, se usa un número basado en 3 para codificar los cubos. El número mínimo de cerdos necesarios es 2 (= Math.log(8, 3).ceil ).

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the minimum number of pigs
// required to find the poisonous bucket
void poorPigs(int buckets,
              int minutesToDie,
              int minutesToTest)
{
    // Print the result
    cout << ceil(log(buckets)
                 / log((minutesToTest
                        / minutesToDie)
                       + 1));
}
 
// Driver Code
int main()
{
    int N = 1000, M = 15, P = 60;
    poorPigs(N, M, P);
 
    return 0;
}

// Java program for the above approach
import java.io.*;
 
class GFG
{
 
  // Function to find the minimum number of pigs
  // required to find the poisonous bucket
  static void poorPigs(int buckets, int minutesToDie,
                       int minutesToTest)
  {
 
    // Print the result
    System.out.print((int)Math.ceil(
      Math.log(buckets)
      / Math.log((minutesToTest / minutesToDie)
                 + 1)));
  }
 
  // Driver Code
  public static void main(String[] args)
  {
    int N = 1000, M = 15, P = 60;
    poorPigs(N, M, P);
  }
}
 
// This code is contributed by Dharanendra L V.

# Python program for the above approach
import  math
 
# Function to find the minimum number of pigs
# required to find the poisonous bucket
def poorPigs(buckets, minutesToDie, minutesToTest):
   
    # Print the result
    print(math.ceil(math.log(buckets)\
                    // math.log((minutesToTest \
                                 // minutesToDie) + 1)));
 
# Driver Code
if __name__ == '__main__':
    N = 1000;
    M = 15;
    P = 60;
    poorPigs(N, M, P);
 
# This code is contributed by 29AjayKumar

// C# program for the above approach
using System;
class GFG
{
 
  // Function to find the minimum number of pigs
  // required to find the poisonous bucket
  static void poorPigs(int buckets, int minutesToDie,
                       int minutesToTest)
  {
 
    // Print the result
    Console.WriteLine((int)Math.Ceiling(
      Math.Log(buckets)
      / Math.Log((minutesToTest / minutesToDie)
                 + 1)));
  }
 
  // Driver Code
  static public void Main()
  {
    int N = 1000, M = 15, P = 60;
    poorPigs(N, M, P);
  }
}
 
// This code is contributed by jana_sayantan.

<script>
// Javascript program for the above approach
 
  // Function to find the minimum number of pigs
  // required to find the poisonous bucket
  function poorPigs(buckets, minutesToDie,
                       minutesToTest)
  {
  
    // Print the result
    document.write(Math.ceil(
      Math.log(buckets)
      / Math.log((minutesToTest / minutesToDie)
                 + 1)));
  }
 
    // Driver Code
    let N = 1000, M = 15, P = 60;
    poorPigs(N, M, P);
 
// This code is contributed by souravghosh0416.
</script>

5

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)