Dados cuatro enteros fuenteX , fuenteY , destinoX y destinoY que representan las coordenadas de origen y destino en un tablero de ajedrez. La tarea es encontrar el número mínimo de movimientos requeridos por el rey para llegar desde el origen hasta el destino.
Un rey puede moverse al cuadrado que tiene un lado común o un vértice común con el cuadrado en el que se encuentra actualmente el rey (generalmente hay 8 cuadrados diferentes a los que puede moverse).
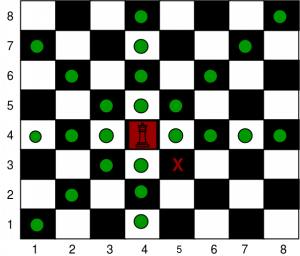
Imprima la ruta usando L, R, U, D, LU, LD, RU y RD donde L, R, U y D representan izquierda, derecha, arriba y abajo respectivamente.
Ejemplos:
Entrada: fuenteX = 4, fuenteY = 4, destinoX = 3, destinoY = 5
Salida: 1
DREntrada: fuenteX = 4, fuenteY = 4, destinoX = 7, destinoY = 0
Salida: 4
UL
UL
UL
L
Aproximación: muévete en dirección diagonal hacia el destino hasta que el rey alcance la misma columna o la misma fila que el destino, luego muévete hacia el destino en línea recta.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to Find the minimum number of moves required to
// reach the destination by the king in a chess board
#include <bits/stdc++.h>
using namespace std;
// function to Find the minimum number of moves required to
// reach the destination by the king in a chess board
void MinSteps(int SourceX, int SourceY, int DestX, int DestY)
{
// minimum number of steps
cout << max(abs(SourceX - DestX), abs(SourceY - DestY)) << endl;
// while the king is not in the same row or column
// as the destination
while ((SourceX != DestX) || (SourceY != DestY)) {
// Go up
if (SourceX < DestX) {
cout << 'U';
SourceX++;
}
// Go down
if (SourceX > DestX) {
cout << 'D';
SourceX--;
}
// Go left
if (SourceY > DestY) {
cout << 'L';
SourceY--;
}
// Go right
if (SourceY < DestY) {
cout << 'R';
SourceY++;
}
cout << endl;
}
}
// Driver code
int main()
{
int sourceX = 4, sourceY = 4;
int destinationX = 7, destinationY = 0;
MinSteps(sourceX, sourceY, destinationX, destinationY);
return 0;
}
Java
// Java program to Find the minimum
// number of moves required to reach
// the destination by the king in a
// chess board
import java.io.*;
class GFG
{
// function to Find the minimum number
// of moves required to reach the
// destination by the king in a chess board
static void MinSteps(int SourceX, int SourceY,
int DestX, int DestY)
{
// minimum number of steps
System.out.println(Math.max(Math.abs(SourceX - DestX),
Math.abs(SourceY - DestY)));
// while the king is not in the same
// row or column as the destination
while ((SourceX != DestX) ||
(SourceY != DestY))
{
// Go up
if (SourceX < DestX)
{
System.out.print( 'U');
SourceX++;
}
// Go down
if (SourceX > DestX)
{
System.out.println( 'D');
SourceX--;
}
// Go left
if (SourceY > DestY)
{
System.out.print( 'L');
SourceY--;
}
// Go right
if (SourceY < DestY)
{
System.out.print( 'R');
SourceY++;
}
System.out.println();
}
}
// Driver code
public static void main (String[] args)
{
int sourceX = 4, sourceY = 4;
int destinationX = 7, destinationY = 0;
MinSteps(sourceX, sourceY,
destinationX, destinationY);
}
}
// This code is contributed by inder_verma
Python3
# Python 3 program to Find the minimum number of moves required to
# reach the destination by the king in a chess board
# function to Find the minimum number of moves required to
# reach the destination by the king in a chess board
def MinSteps(SourceX, SourceY, DestX, DestY):
# minimum number of steps
print(max(abs(SourceX - DestX), abs(SourceY - DestY)))
# while the king is not in the same row or column
# as the destination
while ((SourceX != DestX) or (SourceY != DestY)):
# Go up
if (SourceX < DestX):
print('U',end = "")
SourceX += 1
# Go down
if (SourceX > DestX):
print('D',end = "")
SourceX -= 1
# Go left
if (SourceY > DestY):
print('L')
SourceY -= 1
# Go right
if (SourceY < DestY):
print('R',end = "")
SourceY += 1
# Driver code
if __name__ == '__main__':
sourceX = 4
sourceY = 4
destinationX = 7
destinationY = 0
MinSteps(sourceX, sourceY, destinationX, destinationY)
# This code is contributed by
# Surendra_Gangwar
C#
// C# program to Find the minimum
// number of moves required to reach
// the destination by the king in a
// chess board
using System;
class GFG
{
// function to Find the minimum number
// of moves required to reach the
// destination by the king in a chess board
static void MinSteps(int SourceX, int SourceY,
int DestX, int DestY)
{
// minimum number of steps
Console.WriteLine(Math.Max(Math.Abs(SourceX - DestX),
Math.Abs(SourceY - DestY)));
// while the king is not in the same
// row or column as the destination
while ((SourceX != DestX) ||
(SourceY != DestY))
{
// Go up
if (SourceX < DestX)
{
Console.Write( 'U');
SourceX++;
}
// Go down
if (SourceX > DestX)
{
Console.Write( 'D');
SourceX--;
}
// Go left
if (SourceY > DestY)
{
Console.Write( 'L');
SourceY--;
}
// Go right
if (SourceY < DestY)
{
Console.Write( 'R');
SourceY++;
}
Console.WriteLine();
}
}
// Driver code
public static void Main ()
{
int sourceX = 4, sourceY = 4;
int destinationX = 7, destinationY = 0;
MinSteps(sourceX, sourceY,
destinationX, destinationY);
}
}
// This code is contributed by inder_verma
PHP
<?php
// PHP program to Find the minimum
// number of moves required to
// reach the destination by the
// king in a chess board
// function to Find the minimum
// number of moves required to
// reach the destination by the
// king in a chess board
function MinSteps($SourceX, $SourceY,
$DestX, $DestY)
{
// minimum number of steps
echo max(abs($SourceX - $DestX),
abs($SourceY - $DestY)) . "\n";
// while the king is not in the
// same row or column as the destination
while (($SourceX != $DestX) ||
($SourceY != $DestY))
{
// Go up
if ($SourceX < $DestX)
{
echo 'U';
$SourceX++;
}
// Go down
if ($SourceX > $DestX)
{
echo 'D';
$SourceX--;
}
// Go left
if ($SourceY > $DestY)
{
echo 'L';
$SourceY--;
}
// Go right
if ($SourceY < $DestY)
{
echo 'R';
$SourceY++;
}
echo "\n";
}
}
// Driver code
$sourceX = 4; $sourceY = 4;
$destinationX = 7; $destinationY = 0;
MinSteps($sourceX, $sourceY,
$destinationX, $destinationY);
// This code is contributed
// by Akanksha Rai
?>
Javascript
<script>
// Javascript program to Find the minimum
// number of moves required to reach the
// destination by the king in a chess board
// function to Find the minimum number of
// moves required to reach the destination
// by the king in a chess board
function MinSteps(SourceX, SourceY, DestX, DestY)
{
// Minimum number of steps
document.write(Math.max(Math.abs(SourceX - DestX),
Math.abs(SourceY - DestY)) + "<br>");
// While the king is not in the same row
// or column as the destination
while ((SourceX != DestX) ||
(SourceY != DestY))
{
// Go up
if (SourceX < DestX)
{
document.write('U');
SourceX++;
}
// Go down
if (SourceX > DestX)
{
document.write('D');
SourceX--;
}
// Go left
if (SourceY > DestY) {
document.write('L');
SourceY--;
}
// Go right
if (SourceY < DestY)
{
document.write('R');
SourceY++;
}
document.write("<br>");
}
}
// Driver code
let sourceX = 4, sourceY = 4;
let destinationX = 7, destinationY = 0;
MinSteps(sourceX, sourceY, destinationX,
destinationY);
// This code is contributed by souravmahato348
</script>
4 UL UL UL L
Complejidad temporal: O(max(a, b)), donde a = fuenteX y b = fuenteY
Espacio Auxiliar: O(1), ya que no se ha ocupado ningún espacio extra.
Publicación traducida automáticamente
Artículo escrito por pawan_asipu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA