Dado un gráfico dirigido con N vértices con un valor de 0 a N – 1 y N – 1 aristas, la tarea es contar el número de aristas que se deben invertir para que siempre haya una ruta desde cada Node hasta el Node 0 .
Ejemplos:
Entrada: A continuación se muestra el gráfico dado
Salida: 3
Explicación:
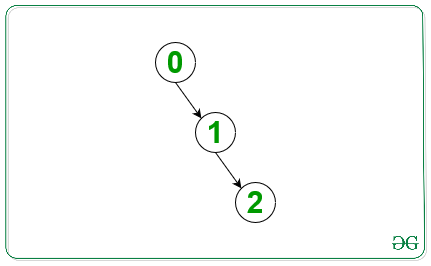
Entrada: A continuación se muestra el gráfico dado
Salida: 0
Enfoque: La idea es usar BFS Traversal para un gráfico . A continuación se muestran los pasos:
- Cree un gráfico dirigido con la dirección de los bordes del gráfico dado invertida.
- Cree una cola y empuje el Node 0 en la cola.
- Durante BFS Traversal en el gráfico, haga lo siguiente:
- Extraiga el Node frontal (por ejemplo, current_node ) de la cola.
- Recorra la lista de adyacencia del Node actual en el gráfico inverso y empuje los Nodes en la cola que no se visitan.
- Recorra la lista de adyacencia del Node actual en el gráfico inverso y empuje los Nodes en la cola que no se visitan.
- El total de Nodes insertados en la cola en los pasos anteriores requiere el conteo de bordes para invertirse porque los Nodes que están conectados al Node actual y aún no han sido visitados en el gráfico no pueden llegar al Node 0, por lo tanto , necesitamos invertir su dirección. Agregue el recuento de los Nodes en el paso anterior al recuento final.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to find minimum reversals
int minRev(vector<vector<int> > edges,
int n)
{
// Add all adjacent nodes to
// the node in the graph
unordered_map<int, vector<int> > graph;
unordered_map<int, vector<int> > graph_rev;
for (int i = 0;
i < edges.size(); i++) {
int x = edges[i][0];
int y = edges[i][1];
// Insert edges in the graph
graph[x].push_back(y);
// Insert edges in the
// reversed graph
graph_rev[y].push_back(x);
}
queue<int> q;
// Create array visited to mark
// all the visited nodes
vector<int> visited(n, 0);
q.push(0);
// Stores the number of
// edges to be reversed
int ans = 0;
// BFS Traversal
while (!q.empty()) {
// Pop the current node
// from the queue
int curr = q.front();
// mark the current
// node visited
visited[curr] = 1;
// Initialize count of edges
// need to be reversed to 0
int count = 0;
q.pop();
// Push adjacent nodes in the
// reversed graph to the queue,
// if not visited
for (int i = 0;
i < graph_rev[curr].size();
i++) {
if (!visited[graph_rev[curr][i]]) {
q.push(graph_rev[curr][i]);
}
}
// Push adjacent nodes in graph
// to the queue, if not visited
// count the number of
// nodes added to the queue
for (int i = 0;
i < graph[curr].size();
i++) {
if (!visited[graph[curr][i]]) {
q.push(graph[curr][i]);
count++;
}
}
// Update the reverse edge
// to the final count
ans += count;
}
// Return the result
return ans;
}
// Driver Code
int main()
{
vector<vector<int> > edges;
// Given edges to the graph
edges = { { 0, 1 }, { 1, 3 }, { 2, 3 },
{ 4, 0 }, { 4, 5 } };
// Number of nodes
int n = 6;
// Function Call
cout << minRev(edges, n);
return 0;
}
Python3
# Python3 program for the above approach # Function to find minimum reversals def minRev(edges, n): # Add all adjacent nodes to # the node in the graph graph = dict() graph_rev = dict() for i in range(len(edges)): x = edges[i][0]; y = edges[i][1]; # Insert edges in the graph if x not in graph: graph[x] = [] graph[x].append(y); # Insert edges in the # reversed graph if y not in graph_rev: graph_rev[y] = [] graph_rev[y].append(x); q = [] # Create array visited to mark # all the visited nodes visited = [0 for i in range(n)] q.append(0); # Stores the number of # edges to be reversed ans = 0; # BFS Traversal while (len(q) != 0): # Pop the current node # from the queue curr = q[0] # mark the current # node visited visited[curr] = 1; # Initialize count of edges # need to be reversed to 0 count = 0; q.pop(0); # Push adjacent nodes in the # reversed graph to the queue, # if not visited if curr in graph_rev: for i in range(len(graph_rev[curr])): if (not visited[graph_rev[curr][i]]): q.append(graph_rev[curr][i]); # Push adjacent nodes in graph # to the queue, if not visited # count the number of # nodes added to the queue if curr in graph: for i in range(len(graph[curr])): if (not visited[graph[curr][i]]): q.append(graph[curr][i]); count += 1 # Update the reverse edge # to the final count ans += count; # Return the result return ans; # Driver Code if __name__=='__main__': edges = [] # Given edges to the graph edges = [ [ 0, 1 ], [ 1, 3 ], [ 2, 3 ],[ 4, 0 ], [ 4, 5 ] ]; # Number of nodes n = 6; # Function Call print(minRev(edges, n)) # This code is contributed by rutvik_56
C#
// C# program for the above approach
using System;
using System.Collections;
using System.Collections.Generic;
class GFG{
// Function to find minimum reversals
static int minRev(ArrayList edges, int n)
{
// Add all adjacent nodes to
// the node in the graph
Dictionary<int,
ArrayList> graph = new Dictionary<int,
ArrayList>();
Dictionary<int,
ArrayList> graph_rev = new Dictionary<int,
ArrayList>();
for(int i = 0;i < edges.Count; i++)
{
int x = (int)((ArrayList)edges[i])[0];
int y = (int)((ArrayList)edges[i])[1];
// Insert edges in the graph
if (!graph.ContainsKey(x))
{
graph[x] = new ArrayList();
}
graph[x].Add(y);
// Insert edges in the
// reversed graph
if (!graph_rev.ContainsKey(y))
{
graph_rev[y] = new ArrayList();
}
graph_rev[y].Add(x);
}
Queue q = new Queue();
// Create array visited to mark
// all the visited nodes
ArrayList visited = new ArrayList();
for(int i = 0; i < n + 1; i++)
{
visited.Add(false);
}
q.Enqueue(0);
// Stores the number of
// edges to be reversed
int ans = 0;
// BFS Traversal
while (q.Count != 0)
{
// Pop the current node
// from the queue
int curr = (int)q.Peek();
// mark the current
// node visited
visited[curr] = true;
// Initialize count of edges
// need to be reversed to 0
int count = 0;
q.Dequeue();
// Enqueue adjacent nodes in the
// reversed graph to the queue,
// if not visited
if (graph_rev.ContainsKey(curr))
{
for (int i = 0;
i < graph_rev[curr].Count;
i++)
{
if (!(bool)visited[(int)(
(ArrayList)graph_rev[curr])[i]])
{
q.Enqueue((int)(
(ArrayList)graph_rev[curr])[i]);
}
}
}
// Enqueue adjacent nodes in graph
// to the queue, if not visited
// count the number of
// nodes added to the queue
if (graph.ContainsKey(curr))
{
for(int i = 0;
i < ((ArrayList)graph[curr]).Count;
i++)
{
if (!(bool)visited[(int)(
(ArrayList)graph[curr])[i]])
{
q.Enqueue((int)(
(ArrayList)graph[curr])[i]);
count++;
}
}
}
// Update the reverse edge
// to the final count
ans += count;
}
// Return the result
return ans;
}
// Driver Code
public static void Main(string []args)
{
ArrayList edges = new ArrayList(){
new ArrayList(){ 0, 1 },
new ArrayList(){ 1, 3 },
new ArrayList(){ 2, 3 },
new ArrayList(){ 4, 0 },
new ArrayList(){ 4, 5 } };
// Number of nodes
int n = 6;
// Function Call
Console.Write(minRev(edges, n));
}
}
// This code is contributed by pratham76
3
Complejidad temporal: O(V+E) donde V es el número de vértices, E es el número de aristas.
Espacio Auxiliar: O(V) donde V es el número de vértices.
Publicación traducida automáticamente
Artículo escrito por mukulkumar10 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA