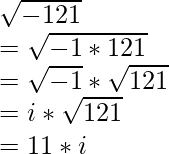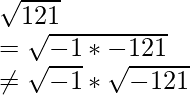En las clases inferiores, se nos enseña que no se puede sacar la raíz cuadrada de números negativos. Sin embargo, podemos sacar la raíz cuadrada de un número negativo, pero implica hacer uso de un nuevo número que se llama número imaginario. Así que supongamos que existe un número i donde: i 2 = -1. Esta i se llama la unidad imaginaria. Podemos observar que hemos creado un sistema numérico completamente nuevo (números complejos), donde la raíz cuadrada de i 2 =-1, e i se llama la unidad imaginaria. Ahora, los números complejos se componen de números reales y puramente imaginarios. Ya estamos familiarizados con los números reales, por ejemplo: 2, 4,03 y π, así que hablemos de números imaginarios puros.
Número puramente imaginario
Un número puramente imaginario es un múltiplo de i. Entonces, -5 i +, 27* i son todos números puramente imaginarios. También se les llama números no reales. Así, un número imaginario es un número que se puede escribir como un número real multiplicado por la unidad imaginaria i . Así, los números complejos son de la forma a + b i , donde a, b son constantes reales . El número complejo a + b i se puede dividir en dos partes, a saber
- La parte real (a)
- Y la parte imaginaria (b) [ no b*i ]
Potencias de la Unidad Imaginaria(i)
Sabemos que i 2 = -1 pero ¿qué pasa con otras potencias de i ?
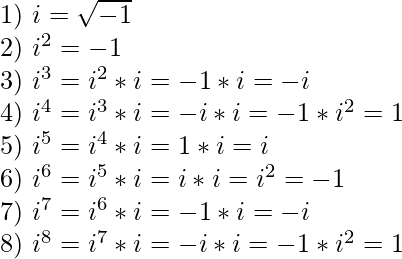
¿Ves el patrón aquí?
Hay un ciclo de i, -1, -i , 1… donde todo múltiplo de 4 es 1.
Para resumir, digamos que i está elevado a la potencia de n.
Si 1) n mod 4 == 0 [la división por 4 deja 0 como resto] entonces la respuesta es 1. por ejemplo: i4 = i8 = i12 = 1
2) n mod 4 == 1 [la división por 4 deja 1 como resto] entonces la respuesta es i . ej.: yo = i5 = i9 = yo
3) n mod 4 == 2 [la división por 4 deja 2 como resto] entonces la respuesta es -1. por ejemplo: i6 = i10 = -1
4) n mod 4 == 3 [la división por 4 deja 3 como resto] entonces la respuesta es -i. por ejemplo: i3 = i7 = -i
Ejemplos:
Simplificar raíces de números negativos
Ejemplo 1: Suponga que se le pide que evalúe la raíz cuadrada de -121.
Ejemplo 2: Suponga que se le pide que evalúe la raíz cuadrada de -(1/9).
Raíz cuadrada principal del número
La raíz cuadrada principal de un número real no negativo es la raíz cuadrada no negativa.
Ejemplo:
La raíz cuadrada principal de a*b no puede descomponerse en la raíz cuadrada principal de a*raíz cuadrada principal de b si tanto a como b son negativos .
Raíz cuadrada principal de -1: La unidad imaginaria se define como i 2 = −1. Usando esta notación, podemos pensar en i como la raíz cuadrada de −1, pero también tenemos (−i) 2 = i 2 = −1 y entonces −i también es una raíz cuadrada de −1. Pero por convención, la raíz cuadrada principal de −1 es i, o más generalmente, si x es cualquier número no negativo, entonces la raíz cuadrada principal de −x es: