Los números que solemos estudiar y que nos han preocupado hasta ahora son los números enteros positivos, 1,2,3, etc., que se usan para contar. Estos se llaman números naturales y han estado con nosotros durante tantos milenios.
Se dice que un famoso matemático Kronecker dijo:
“Dios creó los números naturales; todo lo demás es obra del hombre.”
Luego, las necesidades básicas de la vida llevaron a la creación de fracciones como 3/4, 1/5, etc. A estos números se les llamó números racionales.
Nota: Estos números no se llaman números racionales porque son “razonables”, se llaman racionales porque son razones de números enteros.
Todos estos números se pueden representar en una posición particular en la recta numérica.
Pero hace unos 2500 años, los griegos descubrieron algo más mientras estudiaban geometría. Para su sorpresa, notaron que había algunos números que no podían expresar como números enteros de proporción.
Por ejemplo:
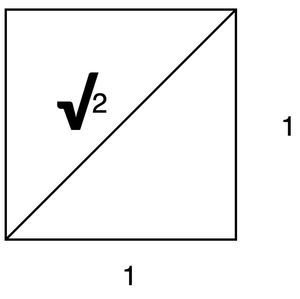
Lo notaron mientras hacían un cuadrado de la unidad de longitud de lado 1. La longitud de la diagonal no se puede representar mediante ninguna proporción de números enteros.
En términos matemáticos modernos, tal número se llama número irracional. Geométricamente significa que no existe una unidad común (por pequeña que sea), tal que el lado y la diagonal del cuadrado son un número entero múltiplo del mismo. De manera similar, la circunferencia de un círculo es un múltiplo irracional del diámetro. Ese múltiplo es «pi».
Ahora definamos formalmente los números racionales y los números irracionales.
Numeros racionales
Un número “x” es un número racional si se puede escribir en la forma “p/q” donde p y q son números enteros (q ≠ 0).
Ejemplo: 25 es un número racional. ¿Cómo? 25 se puede escribir como ![]() donde p = 25 y q = 1. De manera similar, 5.5 también es un número racional, se puede expresar como
donde p = 25 y q = 1. De manera similar, 5.5 también es un número racional, se puede expresar como ![]() y así sucesivamente.
y así sucesivamente.
Numeros irracionales
Un número “x” se llama irracional si no se puede escribir en la forma “p/q” donde p y q son números enteros (q ≠ 0). Así como hay infinitos números racionales, hay infinitos números irracionales.
Ejemplo: √2, √3, ![]()
√2 = 1.41421356237309504880…
![]() = 3.14159265358979323846264338327950…
= 3.14159265358979323846264338327950…
Otra pista para reconocer un número irracional es que el decimal continúa sin repetirse.
Números irracionales populares:
- Pi , π = 3.14159265358979323846264338327950…. Este es un número irracional realmente famoso. La gente ha calculado su valor hasta en cuatrillones de decimales, pero todavía no han encontrado ningún patrón.
- El número de Euler “e” . También es muy popular en matemáticas. En este caso, también, las personas intentaron calcularlo hasta muchos decimales, pero aún así, no se encontró ningún patrón. e = 2.7182818284590452353602874713527 (y más…).
- La proporción áurea . Este es un número irracional que se encuentra en muchos campos como la informática, el diseño, el arte y la arquitectura.
¿Es √2 un número irracional?
Prueba :
Para empezar, supongamos que es un Número Racional
Dado que es racional, se puede representar en la forma más simplificada P/Q donde P/Q son números enteros (Q≠ 0) y P/Q no se puede simplificar más,
Lo que significa que la fracción P/Q es irreducible.
P/Q = √2
Cuadrando ambos lados:
(P/P) 2 = 2
P 2 / Q 2 = 2
P 2 = 2 Q 2
Aquí, está claro que P 2 es divisible por 2. Por lo tanto, P 2 es un número par.
Dado que P 2 es par, P también tiene que ser un número par.
Por lo tanto, P se puede escribir como 2A ya que es divisible por 2.
Poniendo el valor P = 2A, obtendremos:
(2A) 2 = 2Q 2
4A 2 = 2Q 2
2A 2 = Q 2
Aquí, se observa que Q 2 también es un número par, ya que es divisible por 2.
Como Q 2 es par, Q también tiene que ser par. Por lo tanto, tanto P como Q resultaron ser números pares , lo que significa que se pueden simplificar aún más.
Es una Contradicción como ya se definió como una fracción en su forma más simple.
Por lo tanto, √2 no puede ser Racional, es un número Irracional.
Propiedades de los números irracionales
Suma de un número irracional y racional:
La suma de un número irracional y uno racional siempre da un número irracional.
Por ejemplo, se sabe que √2 = 1.41421356237309504880… Ahora √2 + 1 = 2.41421356237309504880…. Esto sigue siendo irracional.
Multiplicación de un número irracional por un número racional distinto de cero.
La multiplicación de cualquier número irracional por cualquier número racional distinto de cero da como resultado un número irracional.
Prueba: Sea x un número irracional y sea y un número racional distinto de cero.
Queremos saber si z = xy es irracional o racional.
Esto se demostrará por contradicción. Supongamos que z es un número racional.
Si z es racional, entonces x = z/y donde tanto z como y son números racionales. Esto hace que x sea un número racional. Esto es una contradicción, lo que significa que la suposición anterior estaba equivocada. Entonces, z siempre será un número irracional.
Producto de dos números irracionales:
Al multiplicar un número racional, no es necesario que el número resultante sea siempre irracional.
- π × π = π 2 es irracional.
- Pero √2 × √2 = 2 es racional.
Suma de dos números irracionales:
La respuesta a esto también es similar a la propiedad anterior. La suma de dos números irracionales es a veces racional a veces irracional.
- 3√2 + 4√3 es irracional.
- (3√2 + 6) + (- 3√2) = 6, esto es racional.
Dato curioso: Aparentemente, Hippasus (uno de los estudiantes de Pitágoras) descubrió los números irracionales cuando intentaba escribir la raíz cuadrada de 2 como una fracción (usando geometría, se cree). En cambio, demostró que la raíz cuadrada de 2 no se puede escribir como una fracción, por lo que es irracional.
¡Pero los seguidores de Pitágoras no podían aceptar la existencia de números irracionales, y se dice que Hippasus fue ahogado en el mar como castigo de los dioses!
misterio de pi
Tomemos un círculo, midamos su circunferencia y dividámoslo por su diámetro. Siempre será una constante si se mide con precisión.
Esta relación constante se denota con el símbolo griego ![]() (leído como pi). Eso es,
(leído como pi). Eso es,
![]()
Es una constante universal importante, ocurre en muchos lugares de nuestro universo y en la vida diaria. No fue creado por humanos, fue descubierto. Descubrimos uno de los lugares donde ocurrió pi, fue la geometría.
Entonces, ¿cuál es el valor de Pi?
π = 3.14159265358979323846264338327950…
No es infinito, es un número irracional.
Nota : a menudo tomamos
como valor Pi, pero es una aproximación.
Ahora uno podría pensar, ¿cómo es pi irracional? Uno puede medir la circunferencia, uno puede medir el diámetro y luego tomar su proporción. Entonces debe ser racional.
En realidad, nadie puede encontrar tal caso, si el diámetro se mide y es racional. Entonces la circunferencia debe ser irracional y viceversa. Entonces, ya sea diámetro o circunferencia. Uno de ellos siempre será irracional. Por lo general, los instrumentos de medición no son lo suficientemente precisos. Si existiera una escala de medición perfecta, diría que al menos uno de los números en la fracción es irracional.
Algunos problemas de muestra sobre números irracionales
Pregunta 1: Estos números entran en la categoría de números irracionales: 5, 3,45, 4,444444…, √9.
Responder:
Estos números mencionados anteriormente no son números irracionales.
- 5 es un número entero y por lo tanto, es racional
- 3.45 es un número con Terminación Decimal y por lo tanto, también es Racional.
- 4.444444… es un Número con Expansión Decimal Repetitiva, es Racional.
- √9 es 3 es decir; la raíz cuadrada de 9 es 3 y 3 es un número entero. Por lo tanto, √9 es Racional.
Pregunta 2: “Todo número real es un número irracional”. ¿Verdadero o falso?
Respuesta :
Falso, todos los números son números reales y todos los números reales no terminales son números irracionales. Por ejemplo 2, 3, 4, etc. son algunos ejemplos de números reales y estos no son irracionales.
Pregunta 3: Determina si los siguientes números son racionales o irracionales.
√3, 74, 8.432432432…, 3.14159265358979…, √11, 55/5.
Respuesta :
74, 8.432432432…, y 55/5(11) son números racionales ya que son enteros o sus expansiones decimales terminan, se repiten.
√3, 3.14159265358979…, y √11 son números irracionales ya que sus expansiones decimales no terminan ni se repiten.
Pregunta 4 : ¿Por qué los números enteros no son números irracionales?
Respuesta :
Los números enteros (ya sean positivos, negativos o cero) no son números irracionales sino racionales, ya que se pueden representar en la forma de fracción más simple P/Q (donde Q ≠ 0).
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA