Los números reales se clasifican en números racionales e irracionales respectivamente. Dados dos enteros p y q, un número racional tiene la forma p/q, donde q > 0. Surge un caso especial cuando q=1 y el número racional simplemente se convierte en un número entero. Por lo tanto, todos los números enteros son números racionales, iguales a p. El número p/q refleja la relación p:q. Algunos ejemplos de números racionales son los números pares e impares, fraccionarios y decimales. Todos los enteros también son números racionales.
Hallar números racionales entre números racionales
Cualquier par de números racionales tiene un número infinito de números racionales entre ellos. Por ejemplo, entre dos números enteros. existe una gran cantidad de números decimales, que se pueden calcular hasta cualquier número de lugares decimales. Dados dos números racionales, f1 y f2, existe un número infinito de números racionales entre ellos. Los números racionales dados se pueden representar en la recta numérica y la solución debe estar entre ellos.
Método del mismo denominador para encontrar números racionales entre números racionales
Supongamos el número racional f1 = p1/q1 y el número racional f2 = p2/q2.
Los siguientes pasos se realizan para encontrar uno o más números racionales entre un par de números racionales dados f1 y f2:
Paso 1: Verifique los valores del denominador de ambas fracciones, es decir, compare los valores de q1 y q2.
Paso 2: si ambos denominadores son iguales, es decir, q1 = q2, luego se comparan los numeradores, es decir, se verifican los valores de p1 y p2.
Paso 3: si los numeradores difieren en un número grande, entonces sumamos cualquier valor entero constante pequeño al numerador más pequeño, manteniendo el mismo denominador. Los números racionales se convierten así en p1/q1 y p2/q1 (ya que q1 = q2). Pueden presentarse dos casos:
- p1 > p2 por una gran cantidad, entonces podemos agregar cualquier valor numérico a p1 tal que sea menor que p2, manteniendo el mismo denominador.
- p1 < p2 por una gran cantidad, entonces podemos agregar cualquier valor numérico a p2 tal que sea menor que p1, manteniendo el mismo denominador.
Paso 4: si los numeradores difieren en un valor pequeño, entonces podemos multiplicar ambos números racionales por un valor constante grande y seguir el primer subpunto, de agregar un entero constante pequeño al numerador más pequeño. Multiplicar los números racionales por valores constantes grandes aumenta la brecha en los valores de p1 y p2.
Problemas de muestra
Ejemplo 1:
Sea f 1 = 2/9
f 2 = 38/9
Encuentra 5 números racionales entre f 1 y f 2.
Solución:

Como los denominadores son iguales, encontramos fracciones sumando 1 a un numerador más pequeño, es decir, f1 numerador = 2.
3/9, 4/9, 5/9, 6/9
Ejemplo 2:
Sea f 1 = 2/9
f 2 = 3/9
Encuentra 7 números racionales
Solución:

Paso 1: Multiplique f 1 y f 2 por 10
Por lo tanto, f’ 1 = 20
90
f’ 2 = 30
90
Paso 2: Ahora podemos encontrar el número requerido de números racionales entre f’ 1 y f’ 2 convertidos :
21 /90, 22/90, 23/90, 24/90, 25/90, 26/90, 27/90
Ejemplo 3:
Sea f 1 = 7/11
f2 = 5/11
Encuentra un número racional entre ellos.
Solución:
Como los denominadores son iguales, encontramos fracciones sumando 1 a un numerador más pequeño, es decir, f 2 numerador = 5.
La fracción requerida es = 6/11
Método de diferente denominador para encontrar números racionales entre números racionales
Supongamos el número racional f1 = p1/q1 y el número racional f2 = p2/q2. Los siguientes pasos se realizan para encontrar uno o más números racionales entre un par de números racionales dados f1 y f2:
Paso 1: Verifique los valores del denominador de ambas fracciones, es decir, compare los valores de q1 y q2.
Paso 2: si los denominadores no son iguales, es decir, q1 ≠ q2, primero igualamos los denominadores tomando el MCM de las dos fracciones o multiplicando sucesivamente los denominadores de cualquiera de las fracciones por el numerador y el denominador de la otra, de modo que el los denominadores se vuelven iguales.
Paso 3: Después de igualar los denominadores, seguimos el método del mismo denominador para calcular los números racionales entre ellos.
Problemas de muestra
Ejemplo 1:
Sea f 1 = 3/5
f 2 = 4/7, encuentra un número racional entre ellos.
Solución:
Como los denominadores son diferentes, tomamos el MCM de los denominadores, para igualar el MCM de ambos números racionales (5, 7) = 35
Por lo tanto f 1 = f 1 * 7 = 21/35
f 2 = f 2 * 5 = 20/35
Dado que las fracciones son dos cercanas, necesitamos aumentar la brecha entre ellas multiplicándolas por un valor constante. Multiplicando ambas fracciones por 10 tenemos,
f1 = 210/350
f2 = 200/350
Ahora dos fracciones entre f 1 y f 2 son ,
201/350 , 202/350
Ejemplo 2:
Sea f 1 = 1/4
f 2 = 1, encuentra un número racional entre ellos.
Solución:
Como los denominadores son diferentes, tomamos el MCM de los denominadores, para igualar el MCM de ambos números racionales (1, 4) = 4
Por lo tanto, f 1 = 1/4
f 2 = 4/4
El número racional entre es 2/4 .
Ejemplo 3:
Sea f 1 = 1/2
f 2 = 1/8, encuentre un número racional entre ellos
Solución:
Dado que los denominadores son diferentes, tomamos el MCM de los denominadores para igualar el MCM de ambos números racionales (2, 8) = 8
Por lo tanto, f 1 = f 1 * 4/4 = 4/8
f 2 = 1/8
Uno de los números racionales requeridos entre 1/8 y 4/8 es 3/8.
Método de fórmula para calcular números racionales
Independientemente de calcular los denominadores de las fracciones, podemos encontrar números racionales entre un par dado de números racionales encontrando la mediana del par dado, es decir, dividiéndolos por la mitad.
Sean f 1 = p 1 /q 2 y f 2 = p 2 /q 2 los dos números racionales
Ahora, los números racionales entre ellos se pueden calcular mediante:
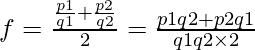
Este método siempre encuentra el número racional exactamente en el medio entre el par dado de números racionales.
Ejemplo 1: Sea f 1 = 1/4
f 2 = 2/4
![]()
Ejemplo 2: Sea f 1 = 1/11
f 2 = 3/8
![]()
Cálculo de MCM de fracciones
⇒ (8+33)/88×2
⇒ 41/176