Numeros reales

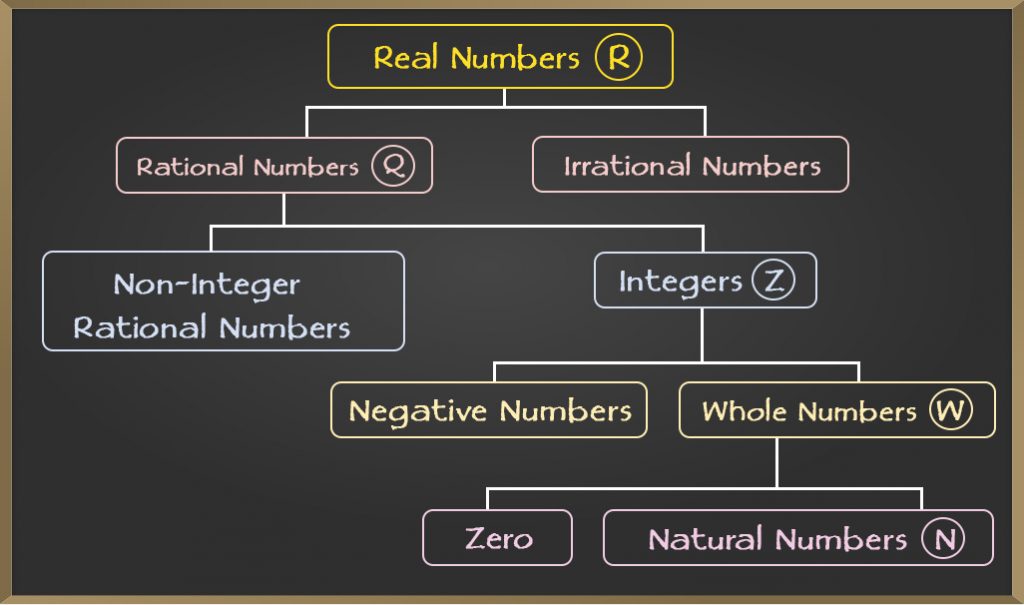
En matemáticas, un número real es un valor de una cantidad continua que puede representar una distancia a lo largo de una línea. Los números reales incluyen tanto los números racionales como los irracionales. Los números racionales como los enteros (-5, 0, 9), las fracciones (1/2, 7/8, 2,5) y los números irracionales como √7, π, etc., son todos números reales.

Alguna vez pensaste que podemos contar cosas, pero ¿cómo podemos contar? Podemos contar mediante el uso de números. Pero el número también es de muchos tipos, algunos tienen valores negativos, algunos tienen valores positivos, algunos son muy grandes, algunos son muy pequeños, algunos están en operaciones matemáticas, por lo que hay muchos tipos de números.

El número o el sistema numeral es el sistema de representación de los números. Hay varios tipos de sistemas numéricos en matemáticas como binario, decimal, etc. El sistema numérico representa cómo se debe escribir un número.

Los números se dividen en los siguientes tipos:

• Números naturales
• números enteros
• enteros
• Numeros racionales
• Numeros irracionales

Números naturales

Los números naturales son aquellos que usas en tu vida diaria para contar como 1, 2, 3… Estos son números positivos porque no podemos contar en términos negativos.

Supongamos que elige un número de 1, 2, 3, 4, 5… y así sucesivamente hasta el infinito. Estos números se conocen como números naturales. Estos números naturales se denotan con el símbolo N.

números enteros

Los números enteros son aquellos números en los que se suma un número a los números naturales. Sumar 0 a los Números Naturales convierte a la serie en un conjunto de Números Enteros.

0, 1, 2, 3, 4, 5… y así hasta el infinito. Estos números se conocen como números enteros. Estos números enteros se denotan con el símbolo W.

enteros

Todos los números que tienen un valor completo se conocen como enteros y hay dos tipos de enteros, el primero es negativo y el segundo es positivo.

….-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5……y así hasta el infinito. Estos números se conocen como números enteros y se denotan con el símbolo Z.

Numeros racionales

En matemáticas, un número racional es un número que se puede expresar como la fracción p/q de dos enteros, un numerador p y un denominador q distinto de cero, como 2/7.

Ejemplo: 25 se puede escribir como 25/1, por lo que es un número racional.

Numeros irracionales

Los números irracionales son aquellos que no se pueden expresar en forma de p/q donde p y q son ambos números enteros y q ≠ 0. En resumen, los números irracionales son números reales que no son números racionales.

Ejemplo: √3, √5, Estos números se conocen como números irracionales.

Pregunta 1. Encuentra tres números racionales entre 6 y 7.

Responder.

Tres números racionales entre 6 y 7 son 13/2, 20/3 27/4.

Pregunta 2. ¿Puede identificar las siguientes series 0, 1, 2, 3, 4, 5, 6, 7 ……?

Responder.

Este es un grupo de números que representan números enteros.

Gráfico de números reales

Representación de Números en la Recta Numérica

Una recta numérica es una representación de números con un intervalo fijo entre ellos en una línea recta. Una línea numérica contiene todos los tipos de números, como números naturales, racionales, enteros, etc.

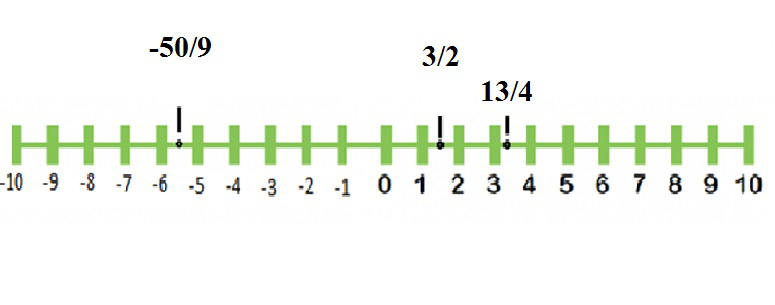
Como se muestra en la línea numérica anterior, el 0 está presente en el medio de la línea. Los enteros positivos se escriben en el lado derecho del cero, mientras que los enteros negativos se escriben en el lado izquierdo del cero.

Los números racionales se escriben entre los números que mienten. Por ejemplo, 3/2 es igual a 1,5, por lo que se anota entre 1 y 2. Muestra que el número 3/2 se encuentra entre 1 y 2.

De manera similar, el número 13/4 se encuentra entre 3 y 4. Así que lo anotamos entre 3 y 4. El número -50/9 se encuentra entre -5 y -6. Así que lo anotamos entre -5 y -6 en la recta numérica.

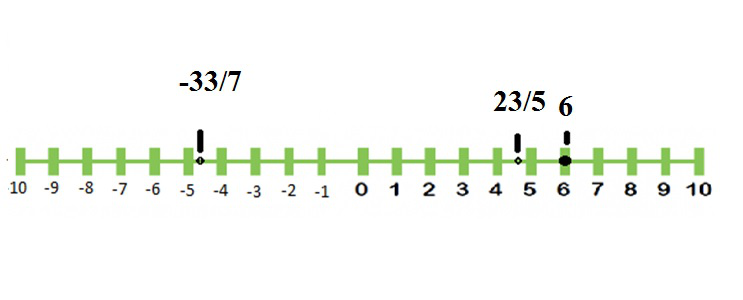
Pregunta: Representa los siguientes números en la recta numérica.

(yo) 23/5

(ii) 6

(iii) -33/7

Expansión decimal de un número real

La expansión decimal de un número real es su representación en base igual a 10 (es decir, en el sistema decimal). En este sistema, cada “lugar decimal” consta de un dígito del 0 al 9. Estos dígitos están ordenados de tal manera que cada dígito se multiplica por una potencia de 10, disminuyendo de izquierda a derecha.

¿Podemos representar 13/4 de otra forma que pueda mostrar su valor exacto en la recta numérica?

La respuesta es sí. Podemos escribirlo en decimales lo que da su valor exacto. Expandámonos 13/4

Entonces 13/4 también se puede escribir como 3.25.

Ahora toma otro ejemplo. Ampliemos 1/3

Así que 1/3 también se puede escribir como 0.3333…… También podemos escribirlo como 

De manera similar, 1/7 se puede escribir como 0.142857142857142857… o  . Esto se puede definir como decimales periódicos.

Ampliación sucesiva

El proceso de representación y visualización de números reales en la recta numérica a través de una lupa se conoce como aumentos sucesivos.

Tomemos un ejemplo de 3.25

Podemos decir que 3,25 definitivamente se encuentra entre 3 y 4. ¿Podemos decir dónde se encuentra exactamente? Sí, podemos hacerlo mediante aumentos sucesivos.

En la primera línea, vemos que 3,25 está entre 3 y 4. Ahora da un paso adelante. Ahora hacemos zoom entre 3.2 y 3.3. Aquí encontramos que 3.25 se encuentra entre 3.2 y 3.3. Entonces representamos 3.25 en la recta numérica usando aumentos sucesivos.

Operaciones con Números Reales

Sabemos que podemos realizar operaciones matemáticas con números racionales. Por ejemplo, podemos sumar, dividir, multiplicar y restar el número racional con otro número. Como resultado, también obtenemos un número racional.

De manera similar, también podemos realizar operaciones matemáticas con números irracionales, pero el resultado puede ser racional o irracional.

Ejemplos de muestra

Ejemplo 1: Suma √3 y √5

Solución:

(√3 + √5)

Ahora la respuesta es un número irracional.

Ejemplo 2: Multiplica √3 y √3.

Solución:

√3 × √3 = 3

Ahora la respuesta es un número racional.

Entonces podemos decir que el resultado de las operaciones matemáticas con números irracionales puede ser racional o irracional.

Ahora suma un número racional con un número irracional.

Ejemplo 3: Sumar 2 y √5

Solución:

(2 + √5)

Ahora la respuesta es un número irracional.

Ejemplo 4: Simplifica la expresión: (2 + √3)(5 + √3)

Solución:

(2 + √3)(5 + √3)

= 10 + 2√3 + 5√3 + 3

= 13 + 7√3

Ahora la respuesta es un número irracional.