Debido a su sencillez, fácil operación, capacidad de protección contra óptimos locales y libre de problemas de derivadas, la metaheurística fue empleada con frecuencia a lo largo de las tres décadas anteriores. La exploración y la explotación son dos características metaheurísticas fundamentales. El primero muestra cómo el algoritmo es capaz de detectar nuevas áreas de búsqueda, mientras que el segundo se concentra en encontrar la solución óptima en un área de búsqueda prometedora. El éxito metaheurístico es aquel que puede equilibrar la exploración con la explotación.
Hay varias clasificaciones para las metaheurísticas.
- Inspirado en la naturaleza versus no inspirado en la naturaleza
- Búsqueda basada en la población frente a punto único
- Función objetivo dinámica frente a función objetivo estática
- Un solo barrio vs. varios barrios
- Uso de memoria frente a métodos sin memoria
Sin embargo, la clasificación inspirada en la naturaleza es ampliamente utilizada. La clasificación inspirada en la naturaleza podría clasificarse en cuatro categorías: técnicas de inteligencia de enjambre, técnicas relacionadas con humanos, técnicas evolutivas y técnicas basadas en la física.
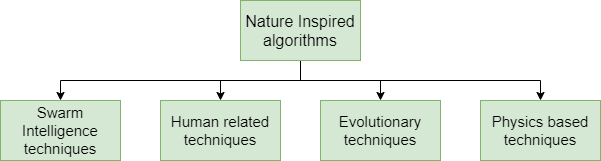
Algunos ejemplos de estos algoritmos inspirados en la naturaleza son la optimización de la solubilidad del gas Henry, la optimización del enjambre de gatos, la optimización basada en la enseñanza y el aprendizaje , etc.
En este artículo, discutiremos la optimización de Dragonfly, que es una técnica de optimización de inteligencia de enjambre.
Inspiración
La optimización Dragonfly tiene fases estáticas y dinámicas análogas a la exploración y explotación, respectivamente, en la optimización metaheurística. En la fase estática, las libélulas crean sub-enjambres y sobrevuelan diferentes áreas. En la fase dinámica, las libélulas vuelan en enjambres más grandes y en una dirección. Según un artículo de investigación publicado por Reynolds en 1987 Bandadas, rebaños y escuelas: un modelo de comportamiento distribuido, un enjambre sigue tres fases básicas:
- Separación: se refiere a la minimización de colisiones estáticas entre entidades en la vecindad de otras.
- Alineación: se refiere a las entidades que igualan la velocidad con la velocidad de otras entidades locales.
- Cohesión: se refiere a la tendencia de las entidades hacia el centro de masa del barrio.
Aparte de estos principios mencionados, la supervivencia es vital en cualquier enjambre que es básicamente de dos formas: ser atraído por las fuentes de alimento y ser repelido por su depredador natural.
Modelo matemático
Definamos los principios mencionados en la sección de inspiración para la optimización de Dragonfly.
Separación:
![]()
donde X , X j denota la posición del individuo actual, j th individuo vecino respectivamente, y N es el número de individuos vecinos.
Alineación:
![]()
donde V j muestra la velocidad del individuo vecino j -ésimo
Cohesión:
![]()
donde X , X j denota la posición del individuo actual, j th individuo vecino respectivamente, y N es el número de individuos vecinos.
Atracción:
![]()
Donde X, X + denotan la posición del individuo actual, fuente de alimento respectivamente.
Repulsión:
![]()
Donde X , X – denota la posición del individuo actual, depredador natural respectivamente.
Se consideran dos vectores para actualizar la posición de las libélulas artificiales en un espacio de búsqueda y simular sus movimientos:
- Vector de paso (
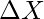 )
) - Vector de posición (
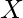 ).
).
El vector de paso denota la dirección del movimiento de las libélulas y se define a continuación como (1):
![]()
donde s, a, c, f, r son los pesos de sus respectivas fases, es decir, separación, alineación, cohesión, atracción, repulsión, w es el peso de inercia y t es el contador de iteraciones.
Alterando los valores de estos pesos se pueden lograr las fases de exploración y explotación.
El vector de posición se calcula simplemente usando el vector de paso como (2):
![]()
Para la fase de exploración, se asigna un peso de cohesión bajo (c) y un peso de alineación alto (a), de manera similar, para la explotación se asigna un peso de alineación bajo (a) y un peso de cohesión alto (c).
El vector de posición da la posición de la libélula; sin embargo, cuando no hay soluciones vecinas, se requiere que las libélulas vuelen en un espacio de búsqueda aleatorio y su posición se actualiza usando la ecuación modificada para el vector de posición (3):
![]()
donde gravamen(d) es:
![]()
donde r1, r2 oscilan en [0,1], \beta es constante, \sigma se calcula de la siguiente manera:
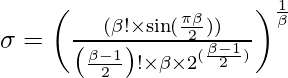
Algoritmo
Inicializar la población de libélulas X i y sus respectivos vectos de paso ![]() para i=1,2,…,n
para i=1,2,…,n
Si bien la iteración no ha terminado o no se ha logrado el resultado optimizado
- Calcular las funciones de aptitud para cada libélula.
- Actualizar los pesos s, a, c, f, r, w y fuentes de alimento, depredador natural
- Calcula Separación (S), Alineación (A), Cohesión (C), Atracción (F) y repulsión (R)
- usando sus ecuaciones
- Si vecino (libélula)
 1
1
- Actualice el vector de velocidad (
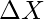 ) y el vector de posición (
) y el vector de posición ( 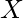 ) usando las ecuaciones 1 y 2
) usando las ecuaciones 1 y 2
- Actualice el vector de velocidad (
- Más
- Actualizar el vector de posición usando la ecuación 3
Terminar mientras
Así es como funciona la optimización de libélula
Referencias: