Optimización multivariante con restricción de igualdad

Wikipedia define la optimización como un problema en el que maximizas o minimizas una función real eligiendo sistemáticamente valores de entrada de un conjunto permitido y calculando el valor de la función. Eso significa que cuando hablamos de optimización siempre estamos interesados ​​en encontrar la mejor solución. Entonces, digamos que uno tiene alguna forma funcional (por ejemplo, en la forma de f(x)) y está tratando de encontrar la mejor solución para esta forma funcional. Ahora bien, ¿qué significa mejor? Uno podría decir que está interesado en minimizar esta forma funcional o maximizar esta forma funcional.

Generalmente, un problema de optimización tiene tres componentes. 
 

minimizar f(x), 
wrt x,  
sujeto a a < x < b 

donde, f(x) : Función objetivo 
x : Variable de decisión 
a < x < b : Restricción 
 

¿Qué es un problema de optimización multivariante? 

En un problema de optimización multivariante, existen múltiples variables que actúan como variables de decisión en el problema de optimización. 
 

z = f(x ₁ , x ₂ , x ₃ … ..x norte ₎

Entonces, cuando observa este tipo de problemas, una función general z podría ser una función no lineal de las variables de decisión x ₁ , x ₂ , x ₃ a x _n . Entonces, hay n variables que uno podría manipular o elegir para optimizar esta función z. Tenga en cuenta que uno podría explicar la optimización univariante usando imágenes en dos dimensiones porque en la dirección x teníamos el valor de la variable de decisión y en la dirección y teníamos el valor de la función. Sin embargo, si se trata de optimización multivariante, entonces tenemos que usar imágenes en tres dimensiones y si las variables de decisión son más de 2, entonces es difícil de visualizar. 

¿Qué es la optimización multivariante con restricción de igualdad ? 
En matemáticas, la igualdad es una relación entre dos cantidades o, más generalmente, dos expresiones matemáticas, afirmando que las cantidades tienen el mismo valor o que las expresiones representan el mismo objeto matemático. Entonces, si se da una función objetivo con más de una variable de decisión y que tiene una restricción de igualdad, esto se conoce como tal. 
Ejemplo : 

min 2x ₁ ² + 4x ₂ ²
st
3x ₁ + 2x ₂ = 12

Aquí x ₁ y x ₂ son dos variables de decisión con restricción de igualdad 3x ₁ + 2x ₂ = 12 

Condición para identificar el punto óptimo en caso de restricción de igualdad 

Si hay un caso de restricción de igualdad, entonces la condición es 
 

-∇ f(x ^* ) = λ ^* ∇ h(x ^* )

Si hay más de un caso de restricción de igualdad, entonces la condición es 
 

-∇ f(x ^* ) = Σ _yo=1 ^l [∇ h _yo (x ^* )] λ _yo ^*

donde, 
f(x ^* ) = f(x ₁ , x ₂ , …., x _n ) = Función objetivo 
h(x ^* ) = h(x ₁ , x ₂ , …., x _n ) = Restricción de igualdad 
λ ^* ∈ R 
 

Resolvamos rápidamente un ejemplo numérico sobre esto para comprender mejor estas condiciones. 

Ejemplo numérico: 
 

Problem:


subject to 





Solution:

Here,

Objective function(f(x)) =  and

Equality constraint(h(x)) = 



For identifying the optimum point we can write the equation as



Hence



Similarly,



According to the condition



This can be written as 

 

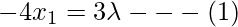
, And we have already the equality constraint equation



By solving these three equations we can get our optimum solution 

along with the value of the variable λ .



Hence  and  is our optimum solution.

¿Por qué las restricciones son importantes en el problema de optimización desde el punto de vista de la ciencia de datos? 

Observamos la optimización desde el punto de vista de la ciencia de datos porque estamos tratando de minimizar los errores. En muchos casos, cuando tratamos de resolver problemas de ciencia de datos y cuando minimizamos el error, dijimos que podríamos usar algún tipo de algoritmo basado en gradiente que llamamos algoritmo de aprendizaje .para resolver el problema. En algunos casos, mientras intentamos minimizar nuestro error o la función objetivo, podemos conocer alguna información sobre el problema que queremos incorporar en la solución. Entonces, si por ejemplo, está tratando de descubrir relaciones entre varias variables y no sabe cuántas relaciones hay, pero sabe con seguridad que existen ciertas relaciones y sabe cuáles son esas relaciones, entonces cuando intente resolver el problema de ciencia de datos, intentaría restringir su problema para que se satisfagan las relaciones conocidas. Entonces, eso podría plantear un problema de optimización donde tiene restricciones en restricciones de igualdad particulares y hay varios otros casos en los que podría tener que mirar la versión de restricción del problema mientras uno resuelve problemas de ciencia de datos. Asi que, es importante entender cómo se resuelven estos problemas. En lugar de problemas de restricciones de igualdad, los problemas de restricciones de desigualdad son más relevantes, por ejemplo, los algoritmos para restricciones de desigualdad son muy útiles en el algoritmo de ciencia de datos que se llamaadmite máquinas vectoriales, etc.