¿Qué es un problema de optimización multivariante?
En un problema de optimización multivariado, existen múltiples variables que actúan como variables de decisión en el problema de optimización.
z = f(x 1 , x 2 , x 3 … ..x norte )
Entonces, cuando observa este tipo de problemas, una función general z podría ser una función no lineal de las variables de decisión x 1 , x 2 , x 3 a x n . Entonces, hay n variables que uno podría manipular o elegir para optimizar esta función z. Tenga en cuenta que uno podría explicar la optimización univariante usando imágenes en dos dimensiones porque en la dirección x teníamos el valor de la variable de decisión y en la dirección y teníamos el valor de la función. Sin embargo, si se trata de optimización multivariante, entonces tenemos que usar imágenes en tres dimensiones y si las variables de decisión son más de 2, entonces es difícil de visualizar.
¿Por qué nos interesan las Condiciones KKT?
Optimización multivariante con restricción de desigualdad : en matemáticas, una desigualdad es una relación que hace una comparación no igual entre dos números u otras expresiones matemáticas. Se usa con mayor frecuencia para comparar dos números en la recta numérica por su tamaño. Hay varias notaciones diferentes que se utilizan para representar diferentes tipos de desigualdades. Entre ellos <, >, ≤, ≥ son la notación popular para representar diferentes tipos de desigualdades. Entonces, si se da una función objetivo con más de una variable de decisión y tiene una restricción de desigualdad, esto se conoce como tal.
Ejemplo :
min 2x 1 2 + 4x 2 2
st
3x 1 + 2x 2 ≤ 12
Aquí x 1 y x 2 son dos variables de decisión con restricción de desigualdad 3x 1 + 2x 2 ≤ 12
Entonces, en el caso de la optimización multivariada con restricciones de desigualdad, las condiciones necesarias para que x̄ * sea el minimizador deben cumplirse las condiciones KKT. Así que estamos interesados en las condiciones de KKT.
Condiciones KKT:
KKT significa Karush-Kuhn-Tucker . En optimización matemática, las condiciones de Karush-Kuhn-Tucker (KKT), también conocidas como condiciones de Kuhn-Tucker , son pruebas de primera derivada (a veces llamadas condiciones necesarias de primer orden ) para que una solución en programación no lineal sea óptima, siempre que algunos se cumplen las condiciones de regularidad.
Por lo tanto, en general, los problemas de optimización multivariada contienen restricciones de igualdad y desigualdad.
z = min f(x̄)
st
h yo (x̄) = 0, i = 1, 2, …m
gramo j (x̄) ≤ 0, j = 1, 2, …l
Aquí tenemos la restricción de igualdad ‘m’ y la restricción de desigualdad ‘l’ .
Estas son las condiciones para que los problemas de optimización multivariada con restricciones de igualdad y desigualdad estén en su valor óptimo.
- Condición 1 :
where,
= Objective function
= Equality constraint
= Inequality constraint
= Scalar multiple for equality constraint
= Scalar multiple for inequality constraint
- Condición 2 :
, for i = 1, ...l
- Esta condición asegura que el óptimo satisfaga las restricciones de igualdad.
- Condición 3 :
, for i = 1, ..., l
- La lambda debe ser un número real, tantos números reales como haya en las restricciones de igualdad.
- Condición 4 :
, j = 1, ..., m
- Al igual que en la condición 2 de que el óptimo satisface las restricciones de igualdad, necesitamos que la restricción de desigualdad también sea satisfecha por el punto óptimo. Entonces esto asegura que el punto óptimo está en la región factible.
- Condición 5 :
- Ahora, esta es la diferencia real entre la condición de restricción de igualdad y la situación de restricción de desigualdad. Y esta condición se conoce como condición de holgura complementaria . Entonces, lo que esto dice es que si tomas un producto de la restricción de desigualdad y la correspondiente
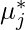 , entonces eso tiene que ser 0. Básicamente, lo que significa es
, entonces eso tiene que ser 0. Básicamente, lo que significa es 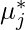 0, en cuyo caso
0, en cuyo caso  es libre de ser cualquier valor tal que esta condición se cumpla o
es libre de ser cualquier valor tal que esta condición se cumpla o  sea 0 en cuyo caso tenemos que calcular
sea 0 en cuyo caso tenemos que calcular 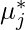 y el
y el 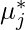 que calculamos tiene que ser tal que sea un número positivo o sea mayor que igual a 0.
que calculamos tiene que ser tal que sea un número positivo o sea mayor que igual a 0.
- Condición 6 :
, j = 1, .., m
- En la condición 5 hemos visto que o bien
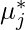 es 0, en cuyo caso
es 0, en cuyo caso  puede ser cualquier valor tal que se cumpla esta condición, o
puede ser cualquier valor tal que se cumpla esta condición, o  es 0, en cuyo caso tenemos que calcular
es 0, en cuyo caso tenemos que calcular 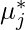 y el
y el 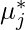 que calculamos tiene que ser tal que sea positivo número o es mayor que igual a 0. Por lo tanto, esta condición está ahí para asegurar que cualquiera que sea el punto óptimo que tenga, no hay posibilidad de más mejoras desde el punto óptimo. Así que esa es la razón por la cual esta condición está ahí.
que calculamos tiene que ser tal que sea positivo número o es mayor que igual a 0. Por lo tanto, esta condición está ahí para asegurar que cualquiera que sea el punto óptimo que tenga, no hay posibilidad de más mejoras desde el punto óptimo. Así que esa es la razón por la cual esta condición está ahí.
Publicación traducida automáticamente
Artículo escrito por AmiyaRanjanRout y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA