Ordenamiento topológico lexicográficamente más pequeño

Dado un grafo dirigido con N vértices y M aristas que pueden contener ciclos, la tarea es encontrar el ordenamiento topológico lexicográficamente más pequeño del grafo si existe; de ​​lo contrario, imprima -1 (si el grafo tiene ciclos). 
El ordenamiento topológico lexigráficamente más pequeño significa que si dos vértices en un gráfico no tienen ningún borde entrante, entonces el vértice con el número más pequeño debe aparecer primero en el ordenamiento. 
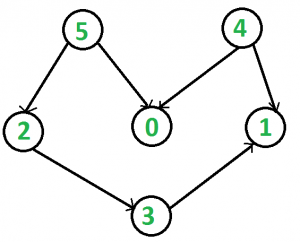
Por ejemplo, en la imagen de abajo son posibles muchos ordenamientos topológicos, por ejemplo, 5 2 3 4 0 1, 5 0 2 4 3 1 . 
Pero el orden más pequeño es 4 5 0 2 3 1 .
Ejemplos: 
 

Aporte: 
 

Salida: 4 5 0 2 3 1 
Aunque 5 4 0 2 3 1 también es una ordenación topológica válida  del grafo dado, pero lexicográficamente 
no es la  más pequeña.

 

Enfoque: Usaremos el algoritmo de Kahn para clasificación topológica con una modificación. En lugar de usar una cola, usaremos un conjunto múltiple para almacenar los vértices para asegurarnos de que cada vez que elijamos un vértice sea el más pequeño posible de todos. La complejidad del tiempo general cambia a 
A continuación es la implementación del enfoque anterior:
 

// C++ implementation of the approach
#include<bits/stdc++.h>
using namespace std;
 
vector<vector<int>> adj;
 
 
// function to add edge to the graph
void addEdge(int x,int y)
{
    adj[x].push_back(y);
}
 
// Function to print the required topological
// sort of the given graph
void topologicalSort()
{
    int V = adj.size();
    // Create a vector to store indegrees of all
    // the vertices
    // Initialize all indegrees to 0
    vector<int> in_degree(V, 0);
  
    // Traverse adjacency lists to fill indegrees of
    // vertices
    // This step takes O(V+E) time
    for (int u = 0; u < V; u++) {
        for (auto x: adj[u])
            in_degree[x]++;
    }
  
    // Create a set and inserting all vertices with
    // indegree 0
    multiset<int> s;
    for (int i = 0; i < V; i++)
        if (in_degree[i] == 0)
            s.insert(i);
  
    // Initialize count of visited vertices
    int cnt = 0;
  
    // Create a vector to store result (A topological
    // ordering of the vertices)
    vector<int> top_order;
  
    // One by one erase vertices from setand insert
    // adjacents if indegree of adjacent becomes 0
    while (!s.empty()) {
  
        // Extract vertex with minimum number from multiset
        // and add it to topological order
        int u = *s.begin();
        s.erase(s.begin());
        top_order.push_back(u);
  
        // Iterate through all its neighbouring nodes
        // of erased node u and decrease their in-degree
        // by 1
        for (auto x:adj[u])
  
            // If in-degree becomes zero, add it to queue
            if (--in_degree[x] == 0)
                s.insert(x);
  
        cnt++;
    }
  
    // Check if there was a cycle
    if (cnt != V) {
        cout << -1;
        return;
    }
  
    // Print topological order
    for (int i = 0; i < top_order.size(); i++)
        cout << top_order[i] << " ";
}
int main()
{
  // number of vertices
  int v = 6;
 
 
  // adjacency matrix
  adj= vector<vector<int>>(v);
 
  addEdge(5,2);
  addEdge(5,0);
  addEdge(4,0);
  addEdge(4,1);
  addEdge(2,3);
  addEdge(3,1);
   
  // find required topological order
  topologicalSort();
}

# Python3 implementation of the approach
import heapq as hq
 
 
 
# function to add edge to the graph
def addEdge(x, y):
    adj[x].append(y)
 
 
# Function to print required topological
# sort of the given graph
def topologicalSort():
    V = len(adj)
    # Create a vector to store indegrees of all
    # the vertices
    # Initialize all indegrees to 0
    in_degree = [0] * V
 
    # Traverse adjacency lists to fill indegrees of
    # vertices
    # This step takes O(V+E) time
    for u in range(V):
        for x in adj[u]:
            in_degree[x] += 1
    # Create a heap and inserting all vertices with
    # indegree 0
    s = []
    for i in range(V):
        if in_degree[i] == 0:
            hq.heappush(s, i)
 
    # Initialize count of visited vertices
    cnt = 0
 
    # Create a vector to store result (A topological
    # ordering of the vertices)
    top_order = []
 
    # One by one erase vertices from setand insert
    # adjacents if indegree of adjacent becomes 0
    while s:
 
        # Extract vertex with minimum number from multiset
        # and add it to topological order
        u = hq.heappop(s)
        top_order.append(u)
 
        # Iterate through all its neighbouring nodes
        # of erased node u and decrease their in-degree
        # by 1
        for x in adj[u]:
            in_degree[x] -= 1
            # If in-degree becomes zero, add it to queue
            if in_degree[x] == 0:
                hq.heappush(s, x)
 
        cnt += 1
 
    # Check if there was a cycle
    if cnt != V:
        print(-1)
        return
 
    # Print topological order
    for i in range(len(top_order)):
        print(top_order[i], end=" ")
 
 
if __name__ == "__main__":
    # number of vertices
    v = 6
 
    # adjacency matrix
    adj = [[] for _ in range(v)]
 
    addEdge(5, 2)
    addEdge(5, 0)
    addEdge(4, 0)
    addEdge(4, 1)
    addEdge(2, 3)
    addEdge(3, 1)
 
    # find required topological order
    topologicalSort()

4 5 0 2 3 1

Complejidad temporal: O(N)
Espacio auxiliar: O(N)