Papel de las probabilidades de registro en la regresión logística

Prerrequisito: probabilidades de registro , regresión logística

NOTA: Se recomienda revisar los temas de requisitos previos para tener una comprensión clara de este artículo.

Las probabilidades logarítmicas juegan un papel importante en la regresión logística, ya que convierte el modelo LR de un modelo basado en probabilidad a un modelo basado en probabilidad. Tanto la probabilidad como las probabilidades logarítmicas tienen su propio conjunto de propiedades; sin embargo, las probabilidades logarítmicas facilitan la interpretación del resultado. Por lo tanto, usar probabilidades logarítmicas es un poco más ventajoso que la probabilidad.

Antes de entrar en los detalles de la regresión logística, comprendamos brevemente qué son las probabilidades.

Probabilidades: En pocas palabras, las probabilidades son las posibilidades de éxito divididas por las posibilidades de fracaso. Se representa en forma de razón. (Como se muestra en la ecuación dada a continuación)

$Odds\ Ratio = \frac{p}{1-p}$

where,
p -> success odds
1-p -> failure odds

Regresión logística con probabilidades de registro

Ahora, entremos en las matemáticas detrás de la participación de las probabilidades logarítmicas en la regresión logística. En la regresión logística, la probabilidad de que la variable independiente corresponda a un éxito está dada por:

$p = \frac{e^{\beta_0 + \beta_1 x}}{1+e^{\beta_0 + \beta_1 x}}$

where, 
p -> odds of success
β_{0, β1 ->} assigned weights 
x -> independent variable

Entonces, las probabilidades de falla en este caso estarán dadas por:

$1-p = 1- \frac{e^{(\beta_0 + \beta_1 x)}}{1+e^{(\beta_0 + \beta_1 x)}} = \frac{1}{1+e^{(\beta_0 + \beta_1 x)}}$

Por lo tanto, la razón de probabilidades se define como:

$\frac{p}{1-p} = \frac{\frac{e^{\beta_0 + \beta_1 x}}{1+e^{\beta_0 + \beta_1 x}}}{\frac{1}{1+e^{(\beta_0 + \beta_1 x)}}} = e^{(\beta_0 + \beta_1 x)}$

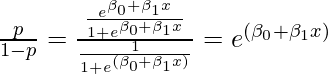
Ahora, como se discutió en el artículo de probabilidades de registro, tomamos el registro de la razón de probabilidades para obtener simetría en los resultados. Por lo tanto, tomando log en ambos lados da:

$\ln(\frac{p}{1-p}) = \beta_0 + \beta_1 x$

que es la ecuación general de la regresión logística. Ahora, en el modelo logístico, LHS contiene el logaritmo de la razón de probabilidades que proporciona el RHS que involucra una combinación lineal de pesos y variables independientes.

Intuición gráfica

i. Problema con salida basada en probabilidad en regresión logística

Consideremos un ejemplo. Digamos que construimos un modelo de regresión logística para determinar la probabilidad de que una persona padezca diabetes en función de su nivel de azúcar. La trama para esto se vería así: (Ver Fig. 1)

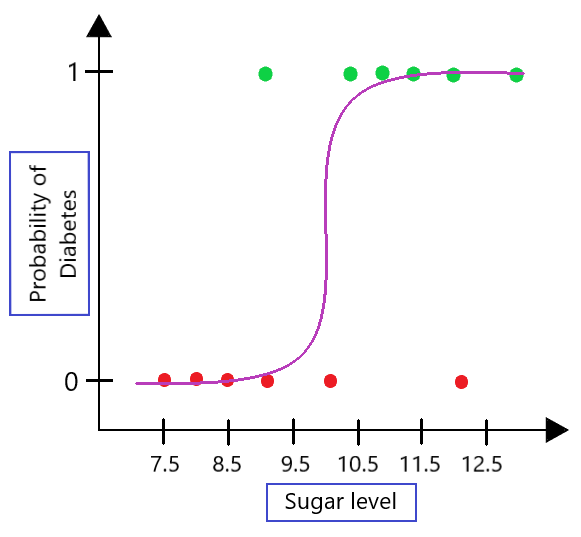
Fig. 1: diagrama del modelo LR

El problema sigue siendo que la salida del modelo es solo binaria según el gráfico anterior. Para abordar este problema, utilizamos el concepto de probabilidades logarítmicas presente en la regresión logística.

ii. Solución: Transformar la salida

Para resolver el problema discutido anteriormente, convertimos la salida basada en probabilidades en una salida basada en probabilidades logarítmicas. (Como se muestra en la ecuación dada a continuación)

$P(diabetes) \rightarrow log (odds\ of\ diabetes) =\log_e(\frac{p}{1-p})$

Supongamos valores aleatorios de p y veamos cómo se transforma el eje y.

una. Valores límite

$At\ (p = 1) \\ \log_e(\frac{p}{1-p}) = \log_e(1/0) \\ = \log_e(1) - \log_e(0) \\ = 0 - (-\infin) \\ = \infin$

$At\ (p = 0) \\ \log_e(\frac{p}{1-p}) = \log_e(0/1) \\ = \log_e(0) - \log_e(1) \\ = (-\infin) - 0 \\ = -\infin$

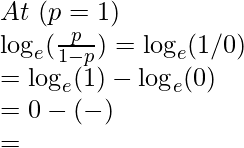
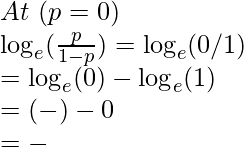
Entonces, el dominio del eje y es: (-∞, ∞)

b. Valor medio

$At\ (p = 0.5) \\ \log_e(\frac{p}{1-p}) = \log_e(0.5/0.5) \\ = \log_e(1)\\ = 0$

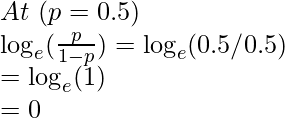
Entonces, en p = 0.5 -> log (probabilidades) = y = 0 .

C. A valores aleatorios

$At\ (p = 0.75) \\ \log_e(\frac{p}{1-p}) = \log_e(0.75/0.25) \\ = \log_e(3)\\ = 1.09$

$At\ (p = 0.3) \\ \log_e(\frac{p}{1-p}) = \log_e(0.3/0.7) \\ = \log_e(3) - \log_e(7)\\ \\ = -0.84$

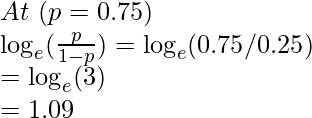
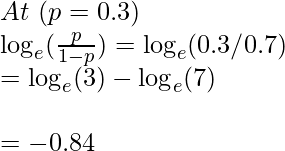
Entonces, en p > 0.5 -> obtenemos el valor de log(odds) en el rango (0, ∞)
y en p < 0.5 -> obtenemos el valor de log(odds) en el rango (-∞, 0)

Si mapeamos estos valores en una gráfica transformada, se vería así: (Como se muestra en la Fig. 2)

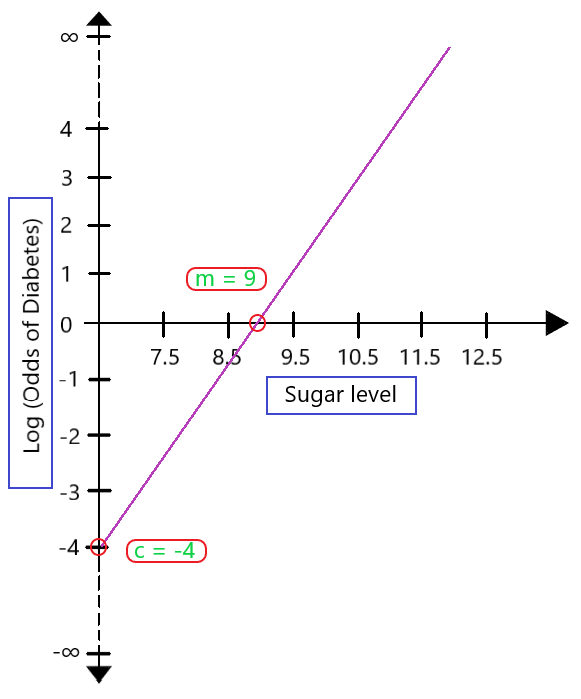
Fig. 2: gráfico LR transformado

Según el valor de la pendiente (m) y la intersección (c), podemos interpretar fácilmente el modelo y obtener resultados deterministas no binarios. Este es el poder de las probabilidades logarítmicas en la regresión logística.

Las probabilidades de registro, comúnmente conocidas como función Logit, se utilizan en los modelos de regresión logística cuando buscamos una salida no binaria. Así es como la regresión logística puede funcionar tanto como modelo de regresión como de clasificación. Para cualquier duda/consulta, comenta abajo.

Publicación traducida automáticamente

Artículo escrito por prakharr0y y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta