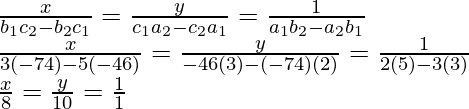Las ecuaciones lineales se utilizan para describir una relación entre dos variables. A veces, en algunas situaciones, no conocemos los valores de las variables que queremos observar. Entonces, luego formulamos las ecuaciones que describen cómo se comportan y las resolvemos. El Número de ecuaciones obtenidas debe ser igual al número de variables. Por ejemplo,
Camus y Bob fueron a una tienda a comprar algunos libros. Camus compró tres copias de «Metamorfosis» y cuatro copias de «Mito de Sísifo». Pagó 500 rupias por estos libros. Luego, Bob compró cuatro copias de Metamorphosis y una copia de «Myth of Sisyphus» en Rs 600. ¿Cómo averiguaría el costo de cada libro?
En situaciones como las anteriores, hacer dos ecuaciones lineales y resolverlas funciona. Hay varias formas de resolver tales pares de ecuaciones.
Par de ecuaciones lineales dos Variables
Una ecuación lineal se define como,
hacha + por + c = 0
Donde a, b y c son números reales y a y b no son cero.
Un par está formado por dos de tales ecuaciones lineales. Se puede representar como,
un 1 x + segundo 1 y + c 1 = 0
un 2 x + segundo 2 y + c 2 = 0
a 1 , b 1 , c 1 , a 2 , b 2 y c 3 son números reales.
Dado que una ecuación lineal representa una línea en el plano cartesiano. Un par representa dos líneas en el plano cartesiano. La solución de este sistema serán los puntos que satisfagan ambas ecuaciones. Hay tres posibilidades en un sistema de este tipo:
- Sin solución
- Solución única
- Infinidad de soluciones

Ninguna solución, solución única e infinitamente muchas soluciones, respectivamente
Veamos brevemente los diferentes métodos para resolver estas ecuaciones.
Métodos gráficos de soluciones
En este método, representamos las ecuaciones en el gráfico y encontramos su intersección a través de él. Buscamos los puntos que son comunes a ambas rectas, a veces solo hay un punto así, pero también puede pasar que no haya soluciones o soluciones infinitas.
Pregunta: Encuentra la intersección de las siguientes líneas.
3x + 5y = 6
x + y = 2
Solución:
Graficaremos ambas líneas en el gráfico.
Estas líneas se cortan en (2,0).
Si comparamos los coeficientes a1, a2, b1, b2, c1 y c2 con diferentes pares de ecuaciones que tienen solución única, infinitas soluciones y ninguna solución. Obtenemos los resultados que se dan a continuación en la tabla.
Para dos líneas,
un 1 x + segundo 1 y + c 1 = 0
un 2 x + segundo 2 y + c 2 = 0
| Representación grafica | Interpretación Algebraica | Condiciones |
| una intersección | Solución única | |
| Líneas Coincidentes | Infinidad de soluciones | |
| Sin intersección/líneas paralelas | Sin solución |
Métodos algebraicos para resolver un par de ecuaciones lineales
Método de sustitución
En este método, usamos una ecuación para expresar una variable en términos de la otra variable, reduciendo así el número de variables en la ecuación. Luego sustituimos esa expresión en la otra ecuación que se nos da.
Pregunta: Resuelva el siguiente par de ecuaciones con el método de sustitución.
x + y = 3
3x + y = 16
Solución:
Escojamos la ecuación
x + y = 3
x = 3 – y
Sustituyendo el valor de x en la otra ecuación,
3x + y = 16
3(3 – y) + y = 16
9 – 3y + y = 16
-2y =7
y = -7/2
Método de eliminación
Este método a veces es más conveniente que el método de sustitución. En este método, eliminamos una variable multiplicando y sumando ecuaciones con constantes adecuadas, esto se hace para eliminar una variable, y cuando la ecuación se queda con una sola variable, se puede resolver fácilmente.
Pregunta: Resuelva las siguientes ecuaciones con el método de eliminación.
x + y = 3
x – y = 5
Solución:
Tenemos dos ecuaciones,
x + y = 3 …….(1)
x – y = 5 …… (2)
Sumando la ecuación (1) y (2) para eliminar la variable -y.
2x = 8
x = 4
Sustituyendo el valor de x en la ecuación (1)
4 + y = 3
y = -1
Método de multiplicación cruzada
Este método parece más complejo que los otros métodos, pero es una de las formas más eficientes de resolver ecuaciones lineales. Digamos las dos rectas cuya ecuación es,
un 1 x + segundo 1 y + c 1 = 0
un 2 x + segundo 2 y + c 2 = 0
En este método de multiplicación cruzada,

La solución está dada por,
![]()
Pregunta 1: Resuelve las siguientes ecuaciones con el método de eliminación.
2x + 3y = 46
3x + 5y = 74
Solución:
a 1 = 2, a 2 = 3, b 1 = 3, b 2 = 5, c 1 = 46 y c 2 = 74
x = 8 y y = 10
Pregunta 2: Resuelva gráficamente el siguiente par de ecuaciones:
2x + 3y = 46
3x + 5y = 74
Solución:
Necesitamos trazarlos en el gráfico por separado y luego mirar su intersección.
Este gráfico interseca son (10,8)
Pregunta 3: Resuelva el siguiente par de ecuaciones lineales con el método de sustitución.
5x + 4y = 20
x + 2y = 4
Solución:
Tenemos que resolver estas dos ecuaciones.
5x + 4y = 20
x + 2y = 4
Elijamos la segunda ecuación,
x = 4 – 2y
Ahora sustituyendo el valor de x en la otra ecuación.
5(4 – 2 años) + 4 años = 20
20 – 10 años + 4 años = 20
-6y = 0
y = 0
Encontrar el valor de x sustituyendo el valor de y en la ecuación,
x = 4 – 2y
x = 4
(4, 0) es la solución a este par de ecuaciones lineales.
Pregunta 4: Resuelve las siguientes ecuaciones con el método de eliminación.
4x + 5y = 20
8x + 2y = 5
Solución:
Sean las ecuaciones,
4x + 5y = 20 ……..(1)
8x + 2y = 5 ….. (2)
Necesitamos eliminar una de las variables aquí de estas dos ecuaciones,
Multiplica la ecuación (1) por 2 y réstala por (2).
2x(1) -(2)
8x + 10y = 40 ….. 2x(1)
8x + 2y = 5 …..(2)
Restando ambos,
8 años = 35
y =
Sustituyendo este valor en la ecuación (1)
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA