Paradoja de cumpleaños – Barcelona Geeks

¿Cuántas personas deben estar en una habitación para que la probabilidad sea del 100% de que al menos dos personas en la habitación tengan el mismo cumpleaños?
Respuesta: 367 (ya que hay 366 cumpleaños posibles, incluido el 29 de febrero).
La pregunta anterior era simple. Pruebe la siguiente pregunta usted mismo.
¿Cuántas personas deben estar en una habitación para que la probabilidad sea del 50% de que al menos dos personas en la habitación tengan el mismo cumpleaños?
Respuesta: 23
El número es sorprendentemente muy bajo. De hecho, solo necesitamos 70 personas para que la probabilidad sea del 99,9 %.
Discutamos la fórmula generalizada.
¿Cuál es la probabilidad de que dos personas entre n tengan el mismo cumpleaños?
Sea P(mismo) la probabilidad de que dos personas en una habitación con n tengan el mismo cumpleaños. P(Igual) se puede evaluar fácilmente en términos de P(diferente) donde P(diferente) es la probabilidad de que todos tengan un cumpleaños diferente.
P(igual) = 1 – P(diferente)
P(diferente) se puede escribir como 1 x (364/365) x (363/365) x (362/365) x …. x (1 – (n-1)/365)
¿Cómo obtuvimos la expresión anterior?
Las personas del primero al último pueden cumplir años en el siguiente orden para que todos los cumpleaños sean distintos:
La primera persona puede tener cualquier cumpleaños entre 365
La segunda persona debe tener un cumpleaños que no sea igual a la primera persona
La tercera persona debe tener un cumpleaños que sea no es lo mismo que las dos primeras personas.
…………….
……………
La n-ésima persona debe tener un cumpleaños que no coincida con ninguna de las personas consideradas anteriormente (n-1).
Aproximación de la expresión
anterior La expresión anterior se puede aproximar utilizando la Serie de Taylor.
$e^{x}=1+x+\frac{x^{2}}{2!}+...$
proporciona una aproximación de primer orden para ex para x << 1:
$e^{x}\approx 1+x$
Para aplicar esta aproximación a la primera expresión derivada para p(diferente), establezca x = -a / 365. Por lo tanto,
$\Large{e^{\frac{-a}{365}}\approx 1-\frac {a}{365}}$
la expresión anterior derivada para p(diferente) puede ser escrito como
1 x (1 – 1/365) x (1 – 2/365) x (1 – 3/365) x …. x (1 – (n-1)/365)
Poniendo el valor de 1 – a/365 como e ^-a/365 , obtenemos lo siguiente.
$\approx 1\times e^{\frac{-1}{365}}\times e^{\frac{-2}{365}}...\times e^{\frac{-(n-1)}{365}}$
$\approx 1\times e^{\frac{-(1+2+...+(n-1))}{365}}$
$\approx 1\times e^{\frac {-(n(n-1))/2}{365}}$
Por lo tanto,
p(igual) = 1- p(diferente)
$\approx 1-e^{-n(n-1)/(2 \times 365)}$
Una aproximación aún más burda viene dada por
p(igual)
$\approx 1-e^{-n^{2}/(2 \times 365)}$
Tomando Log en ambos lados, obtenemos la fórmula inversa.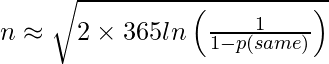
$n \approx \sqrt{2 \times 365 ln\left ( \frac{1}{1-p(same)} \right )}$
Usando la fórmula aproximada anterior, podemos aproximar el número de personas para una probabilidad dada. Por ejemplo, la siguiente función de C++ find() devuelve el n más pequeño para el cual la probabilidad es mayor que el p dado.
Aplicación de fórmula aproximada.
El siguiente es un programa para aproximar el número de personas para una probabilidad dada.

C++

// C++ program to approximate number of people in Birthday Paradox
// problem
#include <cmath>
#include <iostream>
using namespace std;
 
// Returns approximate number of people for a given probability
int find(double p)
{
    return ceil(sqrt(2*365*log(1/(1-p))));
}
 
int main()
{
   cout << find(0.70);
}

Java

// Java program to approximate number
// of people in Birthday Paradox problem
class GFG {
     
    // Returns approximate number of people
    // for a given probability
    static double find(double p) {
         
        return Math.ceil(Math.sqrt(2 *
            365 * Math.log(1 / (1 - p))));
    }
     
    // Driver code
    public static void main(String[] args)
    {
         
        System.out.println(find(0.70));
    }
}
 
// This code is contributed by Anant Agarwal.

Python3

# Python3 code to approximate number
# of people in Birthday Paradox problem
import math
 
# Returns approximate number of
# people for a given probability
def find( p ):
    return math.ceil(math.sqrt(2 * 365 *
                     math.log(1/(1-p))));
 
# Driver Code
print(find(0.70))
 
# This code is contributed by "Sharad_Bhardwaj".

C#

// C# program to approximate number
// of people in Birthday Paradox problem.
using System;
 
class GFG {
      
    // Returns approximate number of people
    // for a given probability
    static double find(double p) {
          
        return Math.Ceiling(Math.Sqrt(2 *
            365 * Math.Log(1 / (1 - p))));
    }
      
    // Driver code
    public static void Main()
    {        
    Console.Write(find(0.70));
    }
}
  
// This code is contributed by nitin mittal.

PHP

<?php
// PHP program to approximate
// number of people in Birthday
// Paradox problem
 
// Returns approximate number
// of people for a given probability
function find( $p)
{
    return ceil(sqrt(2 * 365 *
                     log(1 / (1 - $p))));
}
 
// Driver Code
echo find(0.70);
 
// This code is contributed by aj_36
?>

Javascript

<script>
 
// JavaScript program to approximate number
// of people in Birthday Paradox problem
 
// Returns approximate number of
// people for a given probability
function find( p){
    return Math.ceil(Math.sqrt(2*365*Math.log(1/(1-p))));
}
document.write(find(0.70));
 
</script>

Producción :

Complejidad de tiempo: O (log n)

Espacio Auxiliar: O(1)

Fuente:
http://en.wikipedia.org/wiki/birthday_problem
Aplicaciones:
1) La paradoja del cumpleaños generalmente se analiza con hashing para mostrar la importancia del manejo de colisiones incluso para un pequeño juego de llaves.
2) Ataque de cumpleaños
A continuación se muestra una implementación alternativa en lenguaje C:

C

#include<stdio.h>
int main(){
 
    // Assuming non-leap year
    float num = 365;
 
    float denom = 365;
    float pr;
    int n = 0;
    printf("Probability to find : ");
    scanf("%f", &pr);
 
    float p = 1;
    while (p > pr){
        p *= (num/denom);
        num--;
        n++;
    }
 
    printf("\nTotal no. of people out of which there "
          " is %0.1f probability that two of them "
          "have same birthdays is %d ", p, n);
 
    return 0;
}

C++

// CPP program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
 
int main(){
  
    // Assuming non-leap year
    float num = 365;
  
    float denom = 365;
    float pr;
    int n = 0;
    cout << "Probability to find : " << endl;
    cin >> pr;
  
    float p = 1;
    while (p > pr){
        p *= (num/denom);
        num--;
        n++;
    }
  
    cout <<  " Total no. of people out of which there is " << p
    << "probability that two of them have same birthdays is  "  << n << endl;
  
    return 0;
}
 
// This code is contributed by sanjoy_62.

Java

class GFG{
  public static void main(String[] args){
 
    // Assuming non-leap year
    float num = 365;
 
    float denom = 365;
    double pr=0.7;
    int n = 0;
 
 
    float p = 1;
    while (p > pr){
      p *= (num/denom);
      num--;
      n++;
    }
 
    System.out.printf("\nTotal no. of people out of which there is ");
    System.out.printf( "%.1f probability that two of them "
                      + "have same birthdays is %d ", p, n);
  }
}
 
// This code is contributed by Rajput-Ji

Python3

if __name__ == '__main__':
 
    # Assuming non-leap year
    num = 365;
 
    denom = 365;
    pr = 0.7;
    n = 0;
 
    p = 1;
    while (p > pr):
        p *= (num / denom);
        num -= 1;
        n += 1;
     
 
    print("Total no. of people out of which there is ", end="");
    print ("{0:.1f}".format(p), end="")
    print(" probability that two of them " + "have same birthdays is ", n);
 
# This code is contributed by Rajput-Ji

C#

using System;
public class GFG {
  public static void Main(String[] args) {
 
    // Assuming non-leap year
    float num = 365;
 
    float denom = 365;
    double pr = 0.7;
    int n = 0;
 
    float p = 1;
    while (p > pr) {
      p *= (num / denom);
      num--;
      n++;
    }
 
    Console.Write("\nTotal no. of people out of which there is ");
    Console.Write("{0:F1} probability that two of them have same birthdays is {1} ", p, n);
  }
}
 
// This code is contributed by Rajput-Ji

Javascript

<script>
 
        // Assuming non-leap year
        var num = 365;
 
        var denom = 365;
        var pr = 0.7;
        var n = 0;
 
        var p = 1;
        while (p > pr) {
            p *= (num / denom);
            num--;
            n++;
        }
 
        document.write("\nTotal no. of people out of which there is ");
        document.write(p.toFixed(1)+" probability that two of them " + "have same birthdays is "+ n);
 
// This code is contributed by Rajput-Ji
</script>

Complejidad de tiempo: O (log n)

Espacio Auxiliar: O(1)

Este artículo es una contribución de Shubham . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

PHP

Javascript

C

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta