Permutación – Part 18

Una permutación es una colección o una combinación de objetos de un conjunto donde el orden o la disposición de los objetos elegidos sí importa. En otras palabras, una permutación es una disposición de objetos en un orden definido . Entonces, antes de profundizar en la permutación, primero analicemos brevemente el factorial.

Factorial

• El factorial de un número natural n se denota con la notación n!
• ¡norte! es el producto de todos los números naturales desde 1 hasta n, incluyendo 1 y n.
  es decir, n × (n-1) × (n-2) × (n-3). . . × 1

Ejemplo:

Si n = 3
3! = 3 × 2 × 1 = 6

Si n = 5
5! = 5 × 4 × 3 × 2 × 1 = 120

Si n = 1
1! = 1

Nota: El factorial de 0 se define como 1 por convención, es decir. 0! = 1

¿Por qué utilizar Factorial?

El uso principal del factorial es contar el número de permutaciones (número de formas de ordenar algunos objetos). Entendamos esto con ejemplos.

Ejemplos

Pregunta 1. Una clase tiene solo 3 asientos vacantes. Tres personas P, A y R llegan al mismo tiempo. ¿De cuántas maneras se pueden acomodar P, A y R en esos 3 asientos vacantes?

Solución:

Para el primer asiento, tenemos 3 opciones , es decir, P, A y R.
Seleccionemos aleatoriamente A para el primer asiento.

Para el segundo asiento, tenemos 2 opciones, es decir, P y R
Seleccionemos aleatoriamente R para el segundo asiento.

Para el tercer asiento, tenemos 1 opción, es decir, P

Para resumir, hicimos lo siguiente:
colocamos a una persona en el asiento 1 y colocamos a una persona en el asiento 2 y colocamos a una persona en el asiento 3.
 

El uso de y proviene del hecho de que la ocupación de los 3 asientos era obligatoria.

En matemáticas, y está relacionado con la multiplicación, por lo que podemos decir que el total de opciones = 3 × 2 × 1 = 3.

Si cambiamos el orden de los asientos a P en el primer asiento, A en el segundo asiento y R en el tercero, ¿cambia eso el número total de opciones?

No, no lo hace. Esto se debe a que se da la misma importancia a las tres P, A y R.

Pregunta 2. ¿Encuentre el número de formas de organizar a 5 personas si 2 de ellas siempre se sientan juntas?

Solución:

Consideremos las 2 personas como una unidad y las 3
personas restantes como 3 unidades separadas, por lo que tenemos un total de 4 unidades.

¡La cantidad de formas de organizar estas 4 unidades es 4!
(tal como demostramos en el problema anterior) ¡
La cantidad de formas de colocar a las 2 personas entre ellas es 2!

En conclusión, ¡la cantidad de formas de organizar las 4 unidades y las 2 personas entre sí es 4! × 2!

Pregunta 3. Encuentra todas las palabras de tres letras que comienzan y terminan con una vocal. Dado que no se permite la repetición de alfabetos.

Solución:

Total de vocales en inglés = 7 ( a, e, i, o, u, y, w)
Total de consonantes en inglés = 26 – 7 = 19

1. Las opciones para la primera letra son 7
2. Las opciones para la tercera letra son 6
(ya que se colocó 1 vocal como primera letra)
3. Las opciones para la letra del medio son 19 + (7 – 2) = 24
(19 consonantes + las vocales que no estaban colocadas)

Por lo tanto, las permutaciones totales son 7 × 6 × 24 = 1008

Observe que aquí primero cumplimos la condición de la vocal
para la primera y la tercera letra y luego colocamos la letra del medio.

Permutación

• Si hay n objetos disponibles y organizamos todos, entonces cada arreglo posible se llama permutación.
• Si de n objetos disponibles, elegimos r y los ordenamos. Entonces cada arreglo posible se llama permutación r.
• En la permutación importa el orden de los objetos.

En la permutación, tratamos principalmente con cuatro tipos de problemas

1. Permutación con repetición
2. Permutación sin repetición
3. r – permutación sin repetición
4. r- permutación con repetición

Permutación con repetición

Este es el más simple del lote. En tales problemas, los objetos pueden repetirse. Entendamos estos problemas con algunos ejemplos.

Ejemplos

Pregunta 1. ¿Cuántos números de 3 dígitos mayores de 500 se pueden formar usando 3, 4, 5 y 7?

Solución:

Dado que un número de tres dígitos, mayor que 500 tendrá 5 o 7 en su centésimo lugar, tenemos 2 opciones para este lugar.

No hay restricción en la repetición de los dígitos, por lo que para los 2 dígitos restantes tenemos 4 opciones cada uno

Así que las permutaciones totales son: 2 × 4 × 4 = 32

Pregunta 2. ¿Cuántos números pares que se encuentran entre 1000 y 2000 se pueden formar con los dígitos 1, 2, 4, 5 y 9?

Solución:

Dado que se supone que el número es par, los dígitos en el lugar de las unidades deben ser 2 o 4, lo que nos deja con 2 opciones para el dígito en el lugar de las unidades.

Se supone que el número está entre 1000 y 2000, por lo que los dígitos en el lugar de los mil deben ser 1, por lo que tenemos 
1 opción para el dígito en el lugar de los mil.

El resto de los 2 dígitos puede ser cualquiera de 1, 2, 4, 5 y 9, es decir  , 5 opciones cada uno

Así que las permutaciones totales son: 2 × 5 × 5 × 1 = 50

Permutación sin repetición

En esta clase de problemas no se permite la repetición de objetos. Entendamos estos problemas con algunos ejemplos.

Ejemplos

Pregunta 1. ¿Cuántos números de 3 dígitos divisibles por 3 se pueden formar usando los dígitos 2, 4, 6 y 8 sin repetición?

Solución:

Para que un número sea divisible por 3, la suma de sus dígitos debe ser divisible por 3

A partir del conjunto dado, se pueden formar varios arreglos como 444, pero dado que no se permite la repetición, no los consideraremos.

Nos quedan solo 2 casos, es decir, 2, 4, 6 y 4, 6, 8

El número de arreglos son 3! en cada caso

Por lo tanto, el número total de permutaciones es: 3! + 3! = 12

Pregunta 2. ¿Cuántos números de 4 dígitos divisibles por 5 se pueden formar usando 0, 3, 5, 7 y 9 si no se permite la repetición de dígitos?

Solución:

Para que el número sea divisible por 5, el dígito en el lugar de las unidades debe ser 0 o 5, por lo que tenemos 2 posibilidades.

Caso 1. El dígito en el lugar de las unidades es 0
Hay 4 opciones para el lugar 10 ³ (todos los números excepto el 0)
Hay 3 opciones para el lugar 10 ² (1 se agotó en el lugar 10 ³ )
Hay 2 opciones para el 10 ¹ lugar (1 se agotó en el lugar 10 ³ y 1 en el lugar 10 ² )

Por lo tanto, los arreglos posibles con 0 en el lugar de las unidades son
4 × 3 × 2 = 24

Caso 2. El dígito en el lugar de las unidades es 5
Hay 3 opciones para el lugar 10 ³ (todas excepto 0 y 5)
Hay 2 opciones para el lugar 10 ² (1 se agotó en el lugar 10 ³ )
Hay 1 opción para el lugar 10 ¹ lugar (1 se agotó en el lugar 10 ³ y 1 en el lugar 10 ² )

Por lo tanto, los arreglos posibles con 5 en el lugar de las unidades son 3 × 2 × 1 = 6

Total de arreglos = Número de arreglos en el caso 1 + Número de arreglos en el caso 2
                                = 24 + 6 = 30

r – Permutación sin repetición

Esto es cuando organizamos solo r objetos de n objetos sin repetición. Entendamos esto con un ejemplo.

Ejemplo. Una heladería tiene 10 sabores de helado. ¿Encuentre la cantidad de formas de preparar un cono de helado con 3 sabores diferentes?

Solución:

Consideremos n = 10 (número total de sabores) y r = 3 (número de sabores diferentes necesarios)

Para el primer sabor tenemos 10 opciones
Para el segundo sabor tenemos 10 – 1 opciones
Para el tercer sabor tenemos 10 – 2 opciones y esto es lo mismo que (n – r + 1)

Los números de arreglo serían: 10 × (10 – 1) × (10 – 3 + 1) = 720

A partir de esto, podemos generalizar que el número de formas de organizar r objetos a partir de n objetos diferentes es:
n × (n – 1) . . . (n – r + 1) = ^norte P _r

Fórmula de permutación ( ⁿ P _r )

Del ejemplo anterior, entendimos que _r
ⁿ P _r = n × (n – 1) . . . (n-r + 1) 

¡Multiplicando y dividiendo por (n – r)!
^norte PAGS _r = norte × (n – 1) × (n – 2) × . . . × (n – r + 1) × (n – r)! / (n – r)!

^norte PAGS _r = norte × (n – 1) × (n – 2) × . . . × (n – r + 1) × (n – r) × (n – r – 1) × . . . × 1 / (n – r)!

_norte PAG ^r = norte! / (n – r)! donde 0 ≤ r ≤ norte

Pregunta 1. Encuentra ⁶ P ₃ ?

Solución:

Según la fórmula anterior:
⁶ P ₃ = 6! / (3!) = 6 × 5 × 4 = 120

Pregunta 2. 10 atletas olímpicos están corriendo una carrera. ¿ Encuentra los diferentes arreglos posibles del ^1er , ^2do y 3er ^lugar ?

Solución:

Tenemos que encontrar diferentes arreglos de 10 tomados de 3 a la vez.
Aquí n = 10
         r = 3

¹⁰ P ₃ = 10! / (7!) = 10 × 9 × 8 = 720

Pregunta 3. ¿Encuentra n si ⁿ P ₂ = 12?

Solución:

_norte PAG ^r = norte! / (n – r)! nP ₂ = n
^! / (n – 2)!
      = n × (n – 1) × (n – 2)! / (n – 2)!
      = norte × (n – 1)
      = norte ² – norte

∴ norte ² – norte = 12

Resolviendo la ecuación,
n ² – n – 12 = 0
n (n – 4) + 3 (n – 4) = 0
(n + 3) (n – 4) = 0
∴ n = -3 o n = 4

∵ norte ≥ 0, norte = 4

r – Permutación con repetición

Esto se puede considerar como la distribución de n objetos en r cajas donde se permite la repetición de objetos y cualquier caja puede contener cualquier cantidad de objetos.

La ^1ra  caja puede contener n objetos
La ^2da caja puede contener n objetos
La ^3ra caja puede contener n objetos
. . 
. . 
. . 
La caja r ^-ésima puede contener n objetos

Por lo tanto, el número total de arreglos es:
n × n × n. . . (r veces)
= n ^r

Pregunta 1. Un oficial de policía visita la escena del crimen 3 veces por semana para investigar. ¿Encuentre la cantidad de formas de programar su visita si no hay restricción en la cantidad de visitas por día?

Solución:

La cantidad de formas de programar la primera visita es 7 (cualquiera de los 7 días)
La cantidad de formas de programar la segunda visita es 7 (cualquiera de los 7 días)
La cantidad de formas de programar la tercera visita es 7 (cualquiera de los 7 días ) )

Por lo tanto, la cantidad de formas de programar la primera, la segunda y la tercera visita es 7 × 7 × 7 = 7 ³ = 343

Pregunta 2. ¿De cuántas maneras se pueden colocar 6 reclusos en 4 celdas si cabe cualquier número de reclusos en una celda?

Solución:

El ^1er preso puede ser enviado a cualquiera de las 4 celdas
. El ^2do preso puede ser enviado a cualquiera de las 4 celdas
. .
. .
. .
El 6 ^° recluso puede ser enviado a cualquiera de las 4 celdas

Los arreglos totales son:
4 × 4 × 4 . . . (6 veces) = 4 ⁶

Relación de permutación-combinación

Permutación	Combinación
Una permutación es una forma de ordenar algunos objetos.	Una combinación es una forma de seleccionar objetos.
En la permutación, el orden importa, es decir, ABC y BCA se cuentan por separado .	En combinación, el orden no importa, es decir, ABC y BCA se cuentan como lo mismo.
La permutación de n objetos tomados r a la vez se denota por n P r	La combinación de n objetos tomados r a la vez se denota por n C r

Relación entre ⁿ P _r & ⁿ C _r

Podemos entender ⁿ C _r a través de la siguiente analogía

Considere que tenemos n cajas distintas y r
bolas idénticas. (n > r)

La tarea es colocar todas las bolas r en cajas de modo que ninguna
caja contenga más de 1 bola.

Si las bolas hubieran sido distintas, se trataba de un problema de 
r – permutación sin repetición y entonces la 
respuesta era ⁿ P _r como se discutió anteriormente.

Pero como todos los objetos r son iguales, el r! las formas de disponerlos
pueden considerarse como una sola forma.

Para agrupar todo r! formas de ordenar, dividimos ⁿ P _r por r!

_norte C ^r =      

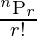
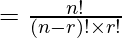
Por lo tanto, la relación entre   ⁿ P _r & ⁿ C _r es:

_norte C ^r =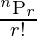 

Ejemplos

Pregunta 1. ¿Cuántas palabras de 4 letras, con o sin significado, se pueden formar con las letras de la palabra ‘SÁBADO’ si no se permite la repetición de letras?

Solución:

La palabra SÁBADO tiene 8 letras, es decir, S, A, T, U, R, D, A e Y

Para formar palabras de 4 letras, primero tenemos que seleccionar 4 letras de estas 8 letras

Las formas de seleccionar 4 letras de 8 letras sin tener en cuenta el orden es ⁸ C ₄ .

Después de la selección, ¡hay 4! preparativos.

Por lo tanto, el número total de palabras formadas es: ⁸ C ₄ × 4!

Nota: 
Seleccionar r objetos de n objetos y luego ordenarlos es lo mismo que r-permutación de n objetos.
Entonces, el resultado anterior se puede obtener directamente usando la fórmula ⁿ P _r donde n = 8 y r = 4

Pregunta 2. Encuentra el número de formas de seleccionar 6 bolas de 4 rojas, 6 azules y 5 blancas dado que la selección debe tener 2 bolas de cada color.

Solución:

Necesitamos seleccionar 2 bolas de color rojo, azul y blanco según la condición dada.

El número de formas de seleccionar 2 bolas rojas es ⁴ C ₂
El número de formas de seleccionar 2 bolas azules es ⁶ C ₂
El número de formas de seleccionar 2 bolas blancas es ⁵ C ₂

Por lo tanto, las formas totales de selección son ⁴ C ₂ × ⁶ C ₂ × ⁵ C ₂   = 900