Dada una string formada por vocales y consonantes. La tarea es encontrar el número de formas en que los caracteres de la string se pueden organizar de manera que no haya dos vocales adyacentes entre sí.
Nota : Dado que No. de vocales <= No. de consonantes .
Ejemplos:
Input: str = "permutation" Output : 907200 Input: str = "geeksforgeeks" Output: 3175200
Enfoque:
considere la string de ejemplo anterior «permutación»:
- Primero coloque todas las consonantes en los lugares alternos como se muestra a continuación:
-- p -- r -- m -- t -- t -- n --
- ¡ Número de formas de colocar las consonantes = 6! / 2! . as
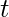aparece dos veces y debe considerarse una vez. - Luego coloque las vocales en las posiciones restantes. Tenemos 7 posiciones restantes y 5 vocales para llenar estos 7 lugares.
Por lo tanto, el número de formas de llenar las vocales =
.
Total no. of ways == 907200
Supongamos que, en una string, el número de vocales es vocalCount y el número de consonantes es consonantCount .
Por lo tanto,
Total de formas = (consonantCount! / duplicateConsonant!) * C (consonantCount+1 , vocalCount) * (vocalCount! / duplicateVowel!)
A continuación se muestra la implementación del enfoque anterior:
C++
// CPP program to count permutations of string
// such that no two vowels are adjacent
#include <bits/stdc++.h>
using namespace std;
// Factorial of a number
int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
// Function to find c(n, r)
int ncr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
// Function to count permutations of string
// such that no two vowels are adjacent
int countWays(string str)
{
int freq[26] = { 0 };
int nvowels = 0, nconsonants = 0;
int vplaces, cways, vways;
// Finding the frequencies of
// the characters
for (int i = 0; i < str.length(); i++)
++freq[str[i] - 'a'];
// finding the no. of vowels and
// consonants in given word
for (int i = 0; i < 26; i++) {
if (i == 0 || i == 4 || i == 8
|| i == 14 || i == 20)
nvowels += freq[i];
else
nconsonants += freq[i];
}
// finding places for the vowels
vplaces = nconsonants + 1;
// ways to fill consonants 6! / 2!
cways = factorial(nconsonants);
for (int i = 0; i < 26; i++) {
if (i != 0 && i != 4 && i != 8 && i != 14
&& i != 20 && freq[i] > 1) {
cways = cways / factorial(freq[i]);
}
}
// ways to put vowels 7C5 x 5!
vways = ncr(vplaces, nvowels) * factorial(nvowels);
for (int i = 0; i < 26; i++) {
if (i == 0 || i == 4 || i == 8 || i == 14
|| i == 20 && freq[i] > 1) {
vways = vways / factorial(freq[i]);
}
}
return cways * vways;
}
// Driver code
int main()
{
string str = "permutation";
cout << countWays(str) << endl;
return 0;
}
Java
// Java program to count permutations of string
// such that no two vowels are adjacent
class GFG
{
// Factorial of a number
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
// Function to find c(n, r)
static int ncr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
// Function to count permutations of string
// such that no two vowels are adjacent
static int countWays(String str)
{
int freq[]=new int[26];
for(int i=0;i<26;i++)
{
freq[i]=0;
}
int nvowels = 0, nconsonants = 0;
int vplaces, cways, vways;
// Finding the frequencies of
// the characters
for (int i = 0; i < str.length(); i++)
++freq[str.charAt(i) - 'a'];
// finding the no. of vowels and
// consonants in given word
for (int i = 0; i < 26; i++) {
if (i == 0 || i == 4 || i == 8
|| i == 14 || i == 20)
nvowels += freq[i];
else
nconsonants += freq[i];
}
// finding places for the vowels
vplaces = nconsonants + 1;
// ways to fill consonants 6! / 2!
cways = factorial(nconsonants);
for (int i = 0; i < 26; i++) {
if (i != 0 && i != 4 && i != 8 && i != 14
&& i != 20 && freq[i] > 1) {
cways = cways / factorial(freq[i]);
}
}
// ways to put vowels 7C5 x 5!
vways = ncr(vplaces, nvowels) * factorial(nvowels);
for (int i = 0; i < 26; i++) {
if (i == 0 || i == 4 || i == 8 || i == 14
|| i == 20 && freq[i] > 1) {
vways = vways / factorial(freq[i]);
}
}
return cways * vways;
}
// Driver code
public static void main(String []args)
{
String str = "permutation";
System.out.println(countWays(str));
}
}
// This code is contributed
// by ihritik
Python3
# Python3 program to count permutations of
# string such that no two vowels are adjacent
# Factorial of a number
def factorial(n) :
fact = 1;
for i in range(2, n + 1) :
fact = fact * i
return fact
# Function to find c(n, r)
def ncr(n, r) :
return factorial(n) // (factorial(r) *
factorial(n - r))
# Function to count permutations of string
# such that no two vowels are adjacent
def countWays(string) :
freq = [0] * 26
nvowels, nconsonants = 0, 0
# Finding the frequencies of
# the characters
for i in range(len(string)) :
freq[ord(string[i]) - ord('a')] += 1
# finding the no. of vowels and
# consonants in given word
for i in range(26) :
if (i == 0 or i == 4 or i == 8
or i == 14 or i == 20) :
nvowels += freq[i]
else :
nconsonants += freq[i]
# finding places for the vowels
vplaces = nconsonants + 1
# ways to fill consonants 6! / 2!
cways = factorial(nconsonants)
for i in range(26) :
if (i != 0 and i != 4 and i != 8 and
i != 14 and i != 20 and freq[i] > 1) :
cways = cways // factorial(freq[i])
# ways to put vowels 7C5 x 5!
vways = ncr(vplaces, nvowels) * factorial(nvowels)
for i in range(26) :
if (i == 0 or i == 4 or i == 8 or i == 14
or i == 20 and freq[i] > 1) :
vways = vways // factorial(freq[i])
return cways * vways;
# Driver code
if __name__ == "__main__" :
string = "permutation"
print(countWays(string))
# This code is contributed by Ryuga
C#
// C# program to count permutations of string
// such that no two vowels are adjacent
using System;
class GFG
{
// Factorial of a number
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
// Function to find c(n, r)
static int ncr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
// Function to count permutations of string
// such that no two vowels are adjacent
static int countWays(String str)
{
int []freq=new int[26];
for(int i=0;i<26;i++)
{
freq[i]=0;
}
int nvowels = 0, nconsonants = 0;
int vplaces, cways, vways;
// Finding the frequencies of
// the characters
for (int i = 0; i < str.Length; i++)
++freq[str[i] - 'a'];
// finding the no. of vowels and
// consonants in given word
for (int i = 0; i < 26; i++) {
if (i == 0 || i == 4 || i == 8
|| i == 14 || i == 20)
nvowels += freq[i];
else
nconsonants += freq[i];
}
// finding places for the vowels
vplaces = nconsonants + 1;
// ways to fill consonants 6! / 2!
cways = factorial(nconsonants);
for (int i = 0; i < 26; i++) {
if (i != 0 && i != 4 && i != 8 && i != 14
&& i != 20 && freq[i] > 1) {
cways = cways / factorial(freq[i]);
}
}
// ways to put vowels 7C5 x 5!
vways = ncr(vplaces, nvowels) * factorial(nvowels);
for (int i = 0; i < 26; i++) {
if (i == 0 || i == 4 || i == 8 || i == 14
|| i == 20 && freq[i] > 1) {
vways = vways / factorial(freq[i]);
}
}
return cways * vways;
}
// Driver code
public static void Main()
{
String str = "permutation";
Console.WriteLine(countWays(str));
}
}
// This code is contributed
// by ihritik
PHP
<?php
// CPP program to count permutations of string
// such that no two vowels are adjacent
// Factorial of a number
function factorial($n)
{
$fact = 1;
for ($i = 2; $i <= $n; $i++)
$fact = $fact * $i;
return $fact;
}
// Function to find c(n, r)
function ncr($n, $r)
{
return factorial($n) / (factorial($r) * factorial($n - $r));
}
// Function to count permutations of string
// such that no two vowels are adjacent
function countWays($str)
{
$freq = array_fill(0,26,NULL);
$nvowels = 0;
$nconsonants = 0;
// Finding the frequencies of
// the characters
for ($i = 0; $i < strlen($str); $i++)
++$freq[ord($str[$i]) - ord('a')];
// finding the no. of vowels and
// consonants in given word
for ($i = 0; $i < 26; $i++) {
if ($i == 0 || $i == 4 || $i == 8
|| $i == 14 || $i == 20)
$nvowels += $freq[$i];
else
$nconsonants += $freq[$i];
}
// finding places for the vowels
$vplaces = $nconsonants + 1;
// ways to fill consonants 6! / 2!
$cways = factorial($nconsonants);
for ($i = 0; $i < 26; $i++) {
if ($i != 0 && $i != 4 && $i != 8 && $i != 14
&& $i != 20 && $freq[$i] > 1) {
$cways = $cways / factorial($freq[$i]);
}
}
// ways to put vowels 7C5 x 5!
$vways = ncr($vplaces, $nvowels) * factorial($nvowels);
for ($i = 0; $i < 26; $i++) {
if ($i == 0 || $i == 4 || $i == 8 || $i == 14
|| $i == 20 && $freq[$i] > 1) {
$vways = $vways / factorial($freq[$i]);
}
}
return $cways * $vways;
}
// Driver code
$str = "permutation";
echo countWays($str)."\n";
return 0;
// this code is contributed by Ita_c.
?>
Javascript
<script>
// Javascript program to count permutations of string
// such that no two vowels are adjacent
// Factorial of a number
function factorial(n)
{
let fact = 1;
for (let i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
// Function to find c(n, r)
function ncr(n,r)
{
return Math.floor(factorial(n) / (factorial(r) * factorial(n - r)));
}
// Function to count permutations of string
// such that no two vowels are adjacent
function countWays(str)
{
let freq=new Array(26);
for(let i=0;i<26;i++)
{
freq[i]=0;
}
let nvowels = 0, nconsonants = 0;
let vplaces, cways, vways;
// Finding the frequencies of
// the characters
for (let i = 0; i < str.length; i++)
++freq[str[i].charCodeAt(0) - 'a'.charCodeAt(0)];
// finding the no. of vowels and
// consonants in given word
for (let i = 0; i < 26; i++) {
if (i == 0 || i == 4 || i == 8
|| i == 14 || i == 20)
nvowels += freq[i];
else
nconsonants += freq[i];
}
// finding places for the vowels
vplaces = nconsonants + 1;
// ways to fill consonants 6! / 2!
cways = factorial(nconsonants);
for (let i = 0; i < 26; i++) {
if (i != 0 && i != 4 && i != 8 && i != 14
&& i != 20 && freq[i] > 1) {
cways = Math.floor(cways / factorial(freq[i]));
}
}
// ways to put vowels 7C5 x 5!
vways = ncr(vplaces, nvowels) * factorial(nvowels);
for (let i = 0; i < 26; i++) {
if (i == 0 || i == 4 || i == 8 || i == 14
|| i == 20 && freq[i] > 1) {
vways = Math.floor(vways / factorial(freq[i]));
}
}
return cways * vways;
}
// Driver code
let str = "permutation";
document.write(countWays(str));
// This code is contributed by rag2127
</script>
Producción:
907200
Complejidad de tiempo: O(|str|)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por SURENDRA_GANGWAR y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA