¿Por qué falla el algoritmo de Dijkstra en pesos negativos?

Algoritmo de Dijkstra : es un algoritmo de búsqueda de gráficos que utiliza un enfoque codicioso para encontrar la ruta más corta desde el Node de origen hasta todos los demás Nodes restantes . Resuelve el problema de la ruta más corta de fuente única para un gráfico ponderado. Este algoritmo realiza un seguimiento de los pesos de los bordes para encontrar la ruta que minimiza la distancia total.

Complejidad de tiempo: O(V + E*log(V)), cuando se usa cola de prioridad (donde V son los Nodes y E son los bordes)

Limitaciones del Algoritmo de Dijkstra : Para que este algoritmo funcione correctamente:

• El gráfico debe ser ponderado y dirigido.
• Los pesos deben ser no negativos.

Ventajas del algoritmo de Dijkstra :

• Tiene una complejidad de tiempo lineal, por lo que puede usarse fácilmente para problemas grandes.
• Es útil para encontrar la distancia más corta, por lo que también se usa en Google Maps y calcula el tráfico.
• Tiene su uso en áreas como redes telefónicas y mapas geográficos.

Desventajas del algoritmo de Dijkstra :

• No puede manejar pesos negativos.
• Sigue una especie de enfoque ciego por lo que hay una pérdida de tiempo.

¿Por qué falla el algoritmo de Dijkstra en pesos negativos?

Tomemos un ejemplo simple para una mejor comprensión de por qué el algoritmo de Dijkstra falla para pesos negativos.

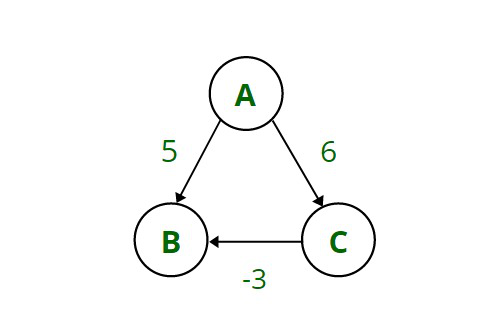
Considere un gráfico dirigido cíclico con Nodes A, B y C que está conectado por bordes que tienen pesos que representan el costo de usar este borde. Los siguientes son los pesos mencionados en el diagrama anterior:

A –>B = 5, A –>C = 6, C –>B = -3 . Aquí un peso C -> B es negativo.

• Considere el Node A como el Node de origen y la tarea es encontrar la distancia más corta desde el Node de origen A hasta todos los demás Nodes presentes en el gráfico, es decir , los Nodes B y C.

• Entonces, primero marque la distancia como 0 , en el Node A (ya que la distancia de A a A es 0 ), y luego marque este Node como visitado, lo que significa que ha sido incluido en el camino más corto.
• Dado que al principio, la distancia del Node de origen a todos los demás Nodes no se conoce, así que inicialícelo como infinito . Actualice esta distancia si se encuentra una distancia más corta que el infinito (que es básicamente el enfoque codicioso)

• Luego, actualice la distancia del Node fuente A a B con el peso del borde que lo conecta con A , que es 5 (porque 5 < infinito).
  De manera similar, actualice también la distancia de A a C , que anteriormente era infinita a 6 (como 6 < infinito).
• Ahora verifique la distancia más corta desde el Node de origen A y como 5 es la distancia mínima de A a B , marque el Node B como ‘ visitado ‘.
  Del mismo modo, el siguiente más corto es 6 , así que marque el Node C también como visitado. En este punto, se visitan los tres Nodes del gráfico.
• Ahora surge aquí el paso más importante, ya que se puede ver que siguiendo este algoritmo, la distancia más corta desde A –> B es 5 pero si se recorre la distancia a través del Node C que es el camino A –> C –> B la distancia será como 3 (como A–>C = 6 y C–>B = -3), entonces 6 + (-3) = 3. Como 3 es menor que 5 , pero el algoritmo de Dijkstra da la respuesta incorrecta como 5 , que no es la distancia más corta. Por lo tanto , el Algoritmo de Dijkstra falla para casos negativos.

Conclusión:

• Dado que Dijkstra sigue un enfoque codicioso, una vez que un Node se marca como visitado, no se puede reconsiderar incluso si hay otro camino con menor costo o distancia. Este problema surge solo si existe un peso o borde negativo en el gráfico.
• Entonces, este algoritmo no puede encontrar la distancia mínima en el caso de pesos negativos , por lo que se usa un algoritmo alternativo de Bellman-Ford para encontrar la distancia más corta en el caso de pesos negativos, ya que detiene el bucle cuando encuentra un ciclo negativo.