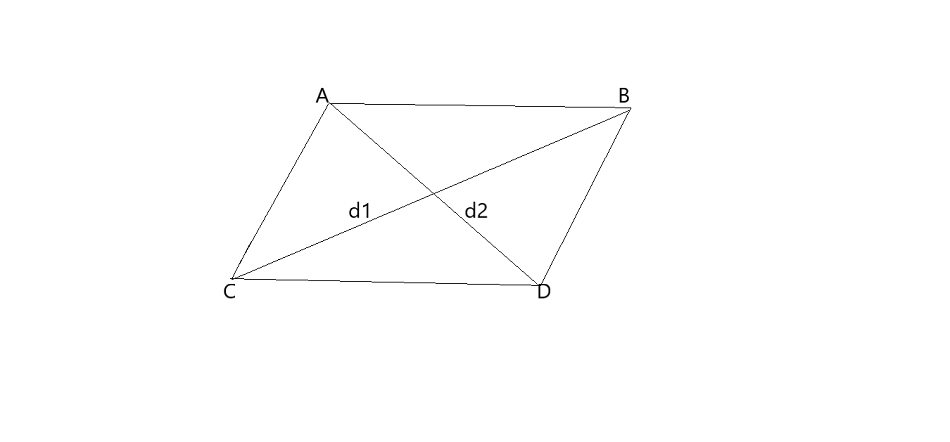
Rombo es un tipo de cuadrilátero. El rombo es el caso especial de un paralelogramo, sus diagonales se cortan entre sí a 90°. También se le llama diamante porque la forma de un rombo es una forma de diamante.
Un cuadrilátero se define como un polígono que tiene cuatro lados y cuatro vértices que encierran cuatro ángulos. La suma de los ángulos interiores de cualquier cuadrilátero es 360°. Son de seis tipos:
- Paralelogramo
- Trapecio
- Cuadrado
- Rectángulo
- Cometa
- Rombo
Rombo
Un rombo se puede definir como un paralelogramo o cuadrilátero especial ya que cumple todas las condiciones de un paralelogramo, un rombo tiene todos sus lados iguales y con dos pares de lados paralelos, pero se puede decir que es un tipo de paralelogramo con cuatro lados congruentes. Por lo tanto, un rombo cumple con todas las propiedades de un paralelogramo. Podemos notar en la siguiente figura que todos los lados mantienen la misma longitud y los lados opuestos permanecen paralelos.
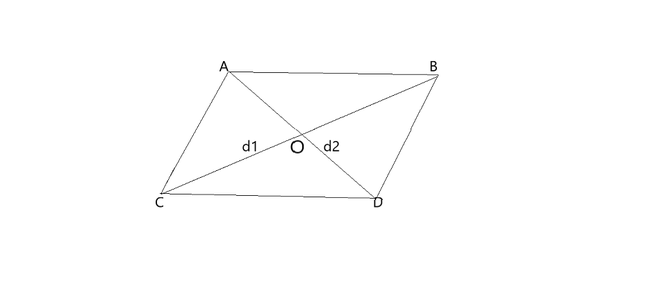
Rombo
¿El cuadrado es un tipo de rombo?
- En Rhombus todos sus lados son iguales y Square también se asemeja a esta propiedad.
- Las diagonales del cuadrado bisecan los ángulos opuestos y perpendiculares entre sí.
Por eso un cuadrado es una especie de rombo.
fórmulas para rombo
Área de Rombo
El área del rombo es la región cubierta dentro del plano o dentro del lado. El área de un rombo está dada por:
Área de Rombo = (d1 x d2)/2 unidades cuadradas
Demuestre que el área de Rombo es (d1 × d2)/2 unidades cuadradas
Prueba:
Considere un triángulo ACD
Área del Triángulo ACD = 1/2 × AD × d1/2 = 1/4 × CD × d1 — (Área del Triángulo = 1/2 × base × altura)
Área del Triángulo ABD = 1/2 × AD × d2/2 = 1/4 × AB × d1
Área del Rombo = Área del Triángulo ACD + Área del Triángulo ABD
= 1/4 × AD × d1 + 1/4 × AD × d1
= 1/4 × AD (d1 + d1)
= 1/4 × AD × 2d1
= 1/2(d1 × d2) (AD = d1)
Por lo tanto, el área de Rombo es (d1 × d2)/2 unidades cuadradas.
perímetro de rombo
El perímetro del rombo es la longitud total de los límites que cubre la longitud, o la suma de todos sus cuatro lados, se llama su perímetro.
Perímetro de Rombo = 4a unidades
Propiedades del rombo
Las siguientes son las propiedades importantes del rombo como:

Propiedades de Rhombus basadas en esta figura
- Los cuatro lados del rombo son iguales (en la figura anterior AB = BC = CD = DA).
- Los lados opuestos de un rombo son paralelos (En la fig. anterior AB //el CD y AC //el BD).
- Los ángulos opuestos de un rombo son iguales (∠C = ∠B y ∠A = ∠D).
- Las diagonales se bisecan entre sí en ángulos rectos (∠COD = ∠DOB = ∠BOA = ∠AOC = 90°).
- Las diagonales de Rombo bisecan los ángulos de un rombo (todos los ángulos son iguales durante la bisección).
- La suma de dos ángulos adyacentes es igual a 180 grados (∠ACD + ∠CDB = 180°).
- Cuatro triángulos rectángulos se forman a partir de dos diagonales de un rombo que son congruentes entre sí.
- Si se unen los puntos medios de las diagonales se forma otro rombo.
- No hay posibilidad de circunscribir un círculo alrededor de un rombo.
- Además, no hay un círculo de inscripción en el rombo.
- Donde los puntos medios de todos los lados se unen, habrá un rectángulo, y las dimensiones, es decir, el largo y el ancho de ese rectángulo del valor principal de la diagonal, por lo tanto, el área del rectángulo es la mitad del rombo.
¿Por qué las diagonales de los rombos no son iguales?
En el rombo, las diagonales son bisectrices perpendiculares entre sí, pero no iguales en longitud. Esto significa que las diagonales se cortan por la mitad.
En un caso especial de rombo, si los 4 ángulos miden 90° cada uno, entonces este es un caso de cuadrado, donde las diagonales tienen la misma medida y son bisectrices perpendiculares entre sí.
Pregunta de muestra
Pregunta 1: Encuentra el área de Rombo, dado que sus diagonales son 9 cm y 8 cm.
Solución:
Área de Rombo = (d1 × d2)/2
= (9 × 8)/2 = 72/2
= 36cm2
Pregunta 2: Si el área del rombo es de 121 cm 2 y la medida de la longitud de la diagonal más larga es de 22 cm, encuentra la diagonal de un rombo.
Solución:
Dado,
Área del rombo = 121 cm 2
decir d1 = 22 cm.
Área del rombo, A = (d1 × d2)/2
121 = (22 × d2)/2
121 = 11 × d2
o d2 = 11 cm
Por lo tanto, la longitud de otra diagonal es de 11 cm.
Pregunta 3: Si el perímetro del rombo es de 120 cm, calcula su longitud.
Solución:
Perímetro de Rombo = 4 × s
120 = 4 × s
o
s = 120/4 = 30
Todos los lados del rombo son iguales = 30 cm
Pregunta 4: Halla el perímetro del rombo si sus diagonales miden 20 y 48 cm.
Solución:
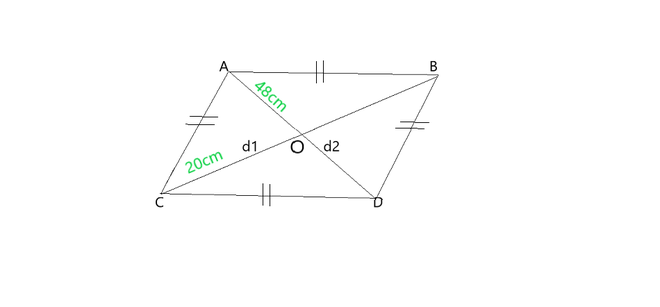
d1 = 20 cm y d2 = 48 cm
OA = DA/2 = 48/2 = 24 cm
CO = BC/2 = 20/2 = 10 cm
En el triángulo AOC
usando el teorema de pitágoras
AC 2 = OA 2 + OC 2
CA = √(24) 2 + (10) 2
CA = √576 + 100 = √676 = 26 cm
Perímetro del rombo = 4×lado = 4×26 = 104cm
Pregunta 5: Encuentra los lados de Rombo, cuya área y altura son 200 cm 2 y 40 cm.
Solución:
Área de rombo = b × h
200 = b × 40
b = 200/40 = 5 cm
Pregunta 6: Encuentra el perímetro del rombo, cuya área es 315 cm 2 y la altura es 15 cm.
Solución:
Área del rombo = b × h
315 = b × 15
b = 315/15 = 21 cm
Perímetro del rombo = 4×lado = 4×21 = 84cm
Pregunta 7: Encuentra la altura de un rombo cuyo área y perímetro son 315 cm 2 y 180 cm 2 respectivamente.
Solución:
Perímetro del rombo = 180cm
4×s = 180
m = 45cm
Área del rombo = b × h
315 = 45 × altura
h = 315/45
alto = 7cm
Publicación traducida automáticamente
Artículo escrito por chauhanishan82 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA