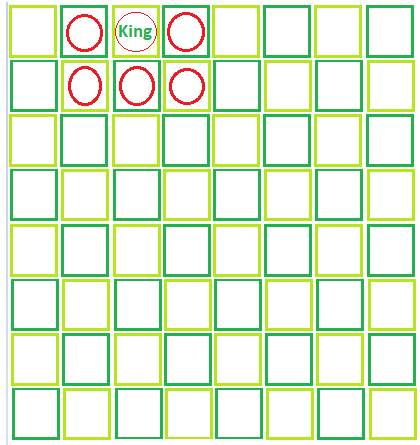
Dado un número entero M , un tablero de ajedrez de 8 * 8 y el rey se coloca en uno de los cuadrados del tablero de ajedrez. Sea la coordenada del rey (R, C) .
Tenga en cuenta que el rey puede moverse a un cuadrado cuya coordenada es (R1, C1) si y solo si se cumple la siguiente condición.
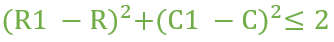
La tarea es contar el número de posiciones a las que puede llegar el rey (excluyendo la posición inicial) desde la casilla dada en exactamente M movimientos.
Ejemplos:
Entrada: fila = 1, columna = 3, movimientos = 1
Salida: número total de posiciones a las que puede llegar el rey = 5
Entrada: fila = 2, columna = 5, movimientos = 2
Salida: número total de posiciones a las que puede llegar el rey = 19
Aproximación: Calcula las coordenadas del cuadrado superior izquierdo que puede visitar el rey (a, b) y las coordenadas del cuadrado inferior derecho (c, d) del tablero de ajedrez que el rey puede visitar. Entonces el número total de celdas que el rey puede visitar será (c – a + 1) * (d – b + 1) – 1 .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of above approach
#include <iostream>
using namespace std;
// Function to return the number of squares that
// the king can reach in the given number of moves
int Square(int row, int column, int moves)
{
int a = 0, b = 0, c = 0, d = 0, total = 0;
// Calculate initial and final coordinates
a = row - moves;
b = row + moves;
c = column - moves;
d = column + moves;
// Since chessboard is of size 8X8 so if
// any coordinate is less than 1 or greater than 8
// make it 1 or 8.
if (a < 1)
a = 1;
if (c < 1)
c = 1;
if (b > 8)
b = 8;
if (d > 8)
d = 8;
// Calculate total positions
total = (b - a + 1) * (d - c + 1) - 1;
return total;
}
// Driver code
int main()
{
int R = 4, C = 5, M = 2;
cout << Square(R, C, M);
return 0;
}
Java
// Java implementation of above approach
class GFG
{
// Function to return the number
// of squares that the king can
// reach in the given number of moves
static int Square(int row, int column,
int moves)
{
int a = 0, b = 0, c = 0,
d = 0, total = 0;
// Calculate initial and final coordinates
a = row - moves;
b = row + moves;
c = column - moves;
d = column + moves;
// Since chessboard is of size 8X8
// so if any coordinate is less
// than 1 or greater than 8 make
// it 1 or 8.
if (a < 1)
a = 1;
if (c < 1)
c = 1;
if (b > 8)
b = 8;
if (d > 8)
d = 8;
// Calculate total positions
total = (b - a + 1) * (d - c + 1) - 1;
return total;
}
// Driver code
public static void main(String []args)
{
int R = 4, C = 5, M = 2;
System.out.println(Square(R, C, M));
}
}
// This code is contributed by Ita_c.
Python3
# Python3 implementation of above approach # Function to return the number of # squares that the king can reach # in the given number of moves def Square(row, column, moves) : a = 0; b = 0; c = 0; d = 0; total = 0; # Calculate initial and final # coordinates a = row - moves; b = row + moves; c = column - moves; d = column + moves; # Since chessboard is of size 8X8 # so if any coordinate is less than # 1 or greater than 8 make it 1 or 8. if (a < 1) : a = 1; if (c < 1) : c = 1; if (b > 8) : b = 8; if (d > 8) : d = 8; # Calculate total positions total = (b - a + 1) * (d - c + 1) - 1; return total; # Driver code if __name__ == "__main__" : R = 4; C = 5; M = 2; print(Square(R, C, M)); # This code is contributed by Ryuga
C#
// C# implementation of above approach
using System;
class GFG
{
// Function to return the number
// of squares that the king can
// reach in the given number of moves
static int Square(int row, int column,
int moves)
{
int a = 0, b = 0, c = 0,
d = 0, total = 0;
// Calculate initial and final coordinates
a = row - moves;
b = row + moves;
c = column - moves;
d = column + moves;
// Since chessboard is of size 8X8
// so if any coordinate is less
// than 1 or greater than 8 make
// it 1 or 8.
if (a < 1)
a = 1;
if (c < 1)
c = 1;
if (b > 8)
b = 8;
if (d > 8)
d = 8;
// Calculate total positions
total = (b - a + 1) * (d - c + 1) - 1;
return total;
}
// Driver code
public static void Main()
{
int R = 4, C = 5, M = 2;
Console.Write(Square(R, C, M));
}
}
// this code is contributed by Ita_c.
PHP
<?php
// PHP implementation of above approach
// Function to return the number of
// squares that the king can reach
// in the given number of moves
function Square($row, $column, $moves)
{
$a = 0; $b = 0; $c = 0;
$d = 0; $total = 0;
// Calculate initial and final coordinates
$a = $row - $moves;
$b = $row + $moves;
$c = $column - $moves;
$d = $column + $moves;
// Since chessboard is of size 8X8 so
// if any coordinate is less than 1
// or greater than 8 make it 1 or 8.
if ($a < 1)
$a = 1;
if ($c < 1)
$c = 1;
if ($b > 8)
$b = 8;
if ($d > 8)
$d = 8;
// Calculate total positions
$total = ($b - $a + 1) *
($d - $c + 1) - 1;
return $total;
}
// Driver code
$R = 4; $C = 5; $M = 2;
echo Square($R, $C, $M);
// This code is contributed
// by Akanksha Rai
?>
Javascript
<script>
// Javascript implementation of above approach
// Function to return the number of squares that
// the king can reach in the given number of moves
function Square(row, column, moves)
{
var a = 0, b = 0, c = 0, d = 0, total = 0;
// Calculate initial and final coordinates
a = row - moves;
b = row + moves;
c = column - moves;
d = column + moves;
// Since chessboard is of size 8X8 so if
// any coordinate is less than 1 or greater than 8
// make it 1 or 8.
if (a < 1)
a = 1;
if (c < 1)
c = 1;
if (b > 8)
b = 8;
if (d > 8)
d = 8;
// Calculate total positions
total = (b - a + 1) * (d - c + 1) - 1;
return total;
}
// Driver code
var R = 4, C = 5, M = 2;
document.write( Square(R, C, M));
// This code is contributed by rrrtnx.
</script>
24
Complejidad de tiempo: O(1)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por Naman_Garg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA